Теорема про нескінченну мавпу
|
Read other articles:

Kathryn Bigelow ai Premi Oscar 2010 Oscar al miglior film 2010 Oscar al miglior regista 2010 Kathryn Ann Bigelow (San Carlos, 27 novembre 1951) è una regista, sceneggiatrice e produttrice cinematografica statunitense. È stata la quarta donna candidata e la prima donna a vincere il premio Oscar al miglior regista,[1] riconoscimento ottenuto nel 2010 per aver diretto e prodotto il film The Hurt Locker, ottenendo anche il premio Oscar al miglior film per il medesimo. Nel 2013 riceve un...

Katedral OnitshaInggris: The Basilica of the Most Holy Trinitycode: en is deprecated LokasiOnitshaNegaraNigeriaDenominasiGereja Katolik RomaSejarahPendiriYang Mulia Mgr. Joseph ShanahanRelikuiBeato Cyprian Iwene TansiArsitekturStatusKatedralStatus fungsionalAktifAdministrasiKeuskupan AgungKeuskupan Agung OnitshaKlerusUskup AgungYang Mulia Uskup Agung Mgr. Valerian OkekeRektorRomo Nwokedi Ezumezu Katedral Onitsha atau yang bernama lengkap Basilika Katedral Tritunggal Mahakudus (Inggris: The Ba...

العلاقات الجنوب سودانية الموريتانية جنوب السودان موريتانيا جنوب السودان موريتانيا تعديل مصدري - تعديل العلاقات الجنوب سودانية الموريتانية هي العلاقات الثنائية التي تجمع بين جنوب السودان وموريتانيا.[1][2][3][4][5] مقارنة بين البلدين هذه �...

Penyuntingan Artikel oleh pengguna baru atau anonim untuk saat ini tidak diizinkan hingga 30 Desember 2025.Lihat kebijakan pelindungan dan log pelindungan untuk informasi selengkapnya. Jika Anda tidak dapat menyunting Artikel ini dan Anda ingin melakukannya, Anda dapat memohon permintaan penyuntingan, diskusikan perubahan yang ingin dilakukan di halaman pembicaraan, memohon untuk melepaskan pelindungan, masuk, atau buatlah sebuah akun. Logo GPR TV Government Public Relation TV (Government Pub...

قرية لي روي الإحداثيات 42°58′39″N 77°59′32″W / 42.9775°N 77.9922°W / 42.9775; -77.9922 [1] تاريخ التأسيس 1797 تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة جينيسي خصائص جغرافية المساحة 2.7 ميل مربع ارتفاع 273 متر عدد السكان عدد �...

Edmund II. Edmund II atau Eadmund II (988/993 – 30 November 1016), dinamai Ironside untuk usahanya menahan invasi Denmark yang dipimpin oleh Raja Canute, adalah raja Inggris dari 23 April sampai 30 November 1016. Referensi Anglo-Saxon Chronicle Clemoes, Peter. The Anglo-Saxons: Studies Presented to Bruce Dickins, 1959 Didahului oleh:Ethelred II Raja Inggris1016 Diteruskan oleh:Canute lbsKepala Negara Monarki Inggris, Skotlandia dan Britania RayaKepala Negara Monarki Ingg...

TodakRentang fosil: 33.9–0 jtyl PreЄ Є O S D C P T J K Pg N Oligosen awal hingga sekarang[1] Status konservasi Hampir Terancam (IUCN 3.1)[2] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Actinopterygii Ordo: Istiophoriformes Famili: XiphiidaeSwainson, 1839 Genus: XiphiasL., 1758 Spesies: X. gladius Nama binomial Xiphias gladiusL., 1758 Persebaran ikan todak (warna biru tua) Sinonim[3] Xiphias imperator Bloch & Schneider, 1801 Tet...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Garis keturunan B.1.640.2 (juga disebut sebagai varian IHU[1]) adalah sebuah garis keturunan SARS-CoV-2, sebuah virus yang menyebabkan Covid-19.[2] Varian tersebut terdeteksi pada Oktober 2021 pada seorang pelancong yang datang dari Ka...

Skip to table of contents This is the talk page for discussing improvements to the Numeral systems template. Put new text under old text. Click here to start a new topic. New to Wikipedia? Welcome! Learn to edit; get help. Assume good faith Be polite and avoid personal attacks Be welcoming to newcomers Seek dispute resolution if needed Archives: 1 Numbers This template is within the scope of WikiProject Numbers, a collaborative effort to improve the coverage of Numbers on Wikipedia. If you wo...

Cet article est une ébauche concernant l’opéra ou l’opérette et la Campanie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Teatro VerdiPrésentationType Théâtre, opéraArchitectes Giuseppe Menichini (d), Antonio D’Amora (d)Ouverture 1872Site web www.teatroverdisalerno.itLocalisationLocalisation Salerne ItalieCoordonnées 40° 40′ 44″ N, 14° 45′ 08″ Emodifi...

Questa voce o sezione sull'argomento storia è stata parzialmente tradotta dalla lingua inglese. Puoi contribuire terminando la traduzione o usando altre fonti. Non usare programmi di traduzione automatica. Usa {{Tradotto da}} quando hai terminato. Se nella pagina di modifica trovi del testo nascosto, controlla che sia aggiornato servendoti dei collegamenti «in altre lingue» in fondo alla colonna di sinistra. Segui i suggerimenti del progetto di riferimento. Q...

Phil BredesenPotret resmi, 2008 Gubernur Tennessee ke-48Masa jabatan18 Januari 2003 – 15 Januari 2011WakilJohn WilderRon RamseyPendahuluDon SundquistPenggantiBill HaslamWalikota Metropolitan Nashville ke-4Masa jabatan27 September 1991 – 24 September 1999PendahuluBill BonerPenggantiBill Purcell Informasi pribadiLahirPhilip Norman Bredesen Jr.21 November 1943 (umur 80)Oceanport, New Jersey, Amerika SerikatPartai politikPartai DemokratSuami/istriSusan Cleaves &#...

American actor (1915–1997) Bill ZuckertZuckert in an episode of Lock-Up (1961)BornWilliam Zuckert(1915-12-18)December 18, 1915The Bronx, New York, U.S.DiedJanuary 23, 1997(1997-01-23) (aged 81)Woodland Hills, California, U.S.OccupationActorYears active1941–1994SpouseGladys HollandChildren3 William Zuckert (December 18, 1915 – January 23, 1997) was an American actor. Early years Born and raised in The Bronx, New York,[1] Zuckert worked in the Office of Indian Af...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Campomarino – news · newspapers · books · scholar · JSTOR (November 2013) Comune in Molise, ItalyCampomarino KëmariniComuneComune di Campomarino Coat of armsLocation of Campomarino CampomarinoLocation of Campomarino in ItalyShow map of ItalyCampomari...

Form of protest Not to be confused with walkout (politics). For the movie, see Walkout (film).Part of a series onOrganized labour Labour movement Conflict theoriesDecent workExploitation of labourTimelineNew unionismProletariatSocial movement unionismSocial democracyDemocratic socialismSocialismCommunismSyndicalismUnion bustingAnarcho-syndicalismNational-syndicalism Labour rights Freedom of association Collective bargaining Child labour Unfree labour Diversity, equity, and inclusion Equal pay...

1998 book by Kiran Desai Hullabaloo in the Guava Orchard First editionAuthorKiran DesaiLanguageEnglishPublisherAtlantic Monthly PressPublication date1998Publication placeIndiaMedia typePrint (hardback & paperback)Pages209ISBN0-87113-711-9OCLC39486434Followed byThe Inheritance of Loss Hullabaloo in the Guava Orchard is a novel by Kiran Desai published in 1998. It is her first book and won the top prize for the Betty Trask Awards in 1998.[1] It is set in the Indian v...
Museum detailing the history of the River Thames and the London Docklands, in London, England Museum of London DocklandsLocation within London Borough of Tower HamletsFormer nameMuseum in DocklandsEstablished2003; 21 years ago (2003)LocationWest India QuayLondonE14EnglandCoordinates51°30′27″N 0°1′25″W / 51.50750°N 0.02361°W / 51.50750; -0.02361Visitors324,438 (2019)[1]DirectorSharon AmentPublic transit accessWest India Quay Website...

Lara Ati 2Nama alternatifLara Ati 2: Mbalik Nang AtiGenre Drama Komedi Skenario Nona Ica Fanni Mardhotilah Murhananto Denny Asse Joni Faisal Cerita Nona Ica Fanni Mardhotilah Murhananto Denny Asse Joni Faisal SutradaraBayu SkakPemeran Bayu Skak Tatjana Saphira Keisya Levronka Dono Pradana Audya Ananta Penggubah lagu temaBayu Skak, Andhika Triyadi, Alvan SeptyLagu pembukaSuwara Atiku oleh Bayu SkakLagu penutupOra Centang Biru oleh Alvan SeptyPenata musik Wiwiex Soedarno Rinaldy Hamid Ne...

Spanish automobile model This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: America Spanish automobile – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) Share of the América Autos SA, issued 30 june 1917 The America was a Spanish automobile manufactured in Barcelona f...
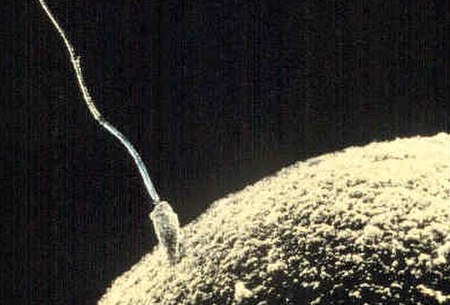
A haploid sex cell Part of a series onSex Biological terms Sexual dimorphism Sexual differentiation Feminization Virilization Sex-determination system XY XO ZW ZO Temperature-dependent Haplodiploidy Heterogametic sex Homogametic sex Sex chromosome X chromosome Y chromosome Testis-determining factor Hermaphrodite Sequential hermaphroditism Simultaneous hermaphroditism Intersex (biology) Mating type Sexual reproduction Evolution of sexual reproduction Anisogamy Isogamy Germ cell Meiosis Gametog...



