Середня довжина шляху
|
Read other articles:

Global System for Mobile Communications AssociationGlobal System for Mobile Communications AssociationTanggal pendirian1995TipeAsosiasi PerusahaanKantor pusatThe Walbrook Buiding Lt. 2, 25 Walbrook, London, Inggris.Bahasa resmi Bahasa InggrisDirektur UmumAnne BouverotSitus webwww.gsma.comGlobal System for Mobile Communications Association adalah asosiasi yang mewadahi kepentingan operator telekomunikasi di seluruh dunia, khususnya operator telekomunikasi yang bergerak di bidang teknologi Glob...

Main article: 2000 United States presidential election 2000 United States presidential election in California ← 1996 November 7, 2000 2004 → Turnout70.94% (of registered voters) 5.41 pp 51.92% (of eligible voters) 0.64 pp[1] Nominee Al Gore George W. Bush Party Democratic Republican Home state Tennessee Texas Running mate Joe Lieberman Dick Cheney Electoral vote 54 0 Popular vote 5,861,203 4,567,429 Percentage 53.45% 41.65% County Resu...

Artikel ini merupakan bagian dari seriKota Vatikan Sejarah Kadipaten Roma (533–751) Donasi Pippin (750-an) Negara Kepausan (754–1870) Annatae Kongregasi untuk Perbatasan Undang-Undang Dasar Pemerintahan Sekuler Negara Gereja Penyerangan Roma oleh Muslim (846) Penaklukan Roma (1870) Tahanan dalam Vatikan (1870–1929) Permasalahan Roma Undang-Undang Jaminan Perjanjian Lateran (1929) Kota Vatikan (1929–sekarang) Gubernur Kota Vatikan Sejarah Gereja Katolik sejak 1962 Sejarah kepausan Inst...

PrologueAlbum studio karya IndyDirilis29 Desember 1996GenrePopLabelCeepee Production Prologue merupakan album musik utama karya Indy. Dirilis pada tahun 1996. Lagu utamanya di album ini adalah Selamat Pagi. Daftar lagu Kupunya Waktu (Tiada Sempurna Dalam Cinta) Berlabuh Prologue Selamat Pagi Bukan Lagu Cinta Titik Seduka Itu Kuakui Prologue (Bila Saja Kau Tahu) Artikel bertopik musik atau lagu Indonesia ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.lbs

Simulasi dari jalur sampel Brownian Motion merupakan instrumen penting dalam menghitung harga instrumen keuangan di bawah ukuran risiko-netral. Komputasi keuangan merupakan cabang ilmu komputer terapan yang menangani masalah praktis di bidang keuangan[1]. Definisi lain yang agak sedikit berbeda menyatakan bahwa komputasi keuangan adalah studi tentang data dan algoritme yang saat ini digunakan di bidang keuangan,[2] serta menghasilkan model atau sistem keuangan.[3] Komp...

Marvel Comics fictional character Comics character VerminVermin as seen in Fear Itself: Spider-Man #1.Publication informationPublisherMarvel ComicsFirst appearanceCaptain America #272 (August 1982)[1]Created byJ. M. DeMatteisMike ZeckIn-story informationAlter egoEdward WhelanSpeciesHuman mutateTeam affiliationsNew RevengersPartnershipsBaron ZemoArmin ZolaAbilities Accomplished geneticist As Vermin: Superhuman strength, speed and stamina Peak level agility, durability and reflexes Extr...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...

ويليام هنري براغ (بالإنجليزية: William Henry Bragg) معلومات شخصية اسم الولادة (بالإنجليزية: William Henry Bragg) الميلاد 2 يوليو 1862 [1][2][3][4][5] الوفاة 12 مارس 1942 (79 سنة) [6][1][2][7] لندن[7] الإقامة أستراليا مواطنة المملكة المتحدة ...
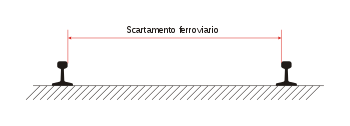
Questa voce o sezione sull'argomento trasporti ha problemi di struttura e di organizzazione delle informazioni. Motivo: Perché lo scartamento ridotto è trattato 2 volte in 2 sezioni? 1) Scartamento ridotto sottosezione di Tipologie 2) In vari titoletti in grassetto di Scartamenti Risistema la struttura espositiva, logica e/o bibliografica dei contenuti. Nella discussione puoi collaborare con altri utenti alla risistemazione. Segui i suggerimenti del progetto di riferimento. Sezione tr...

Official fiat currency of South Africa South African rand List 10 other official names: Suid-Afrikaanse rand (Afrikaans) iRanti yeSewula Afrika (Southern Ndebele) iRanti yoMzantsi Afrika (Xhosa) iRandi laseNingizimu Afrika (Zulu) liRandi laseNingizimu Afrika (Swazi) Ranta ya Afrika Borwa (Northern Sotho) Ranta ya Afrika Borwa (Sotho) Ranta ya Aforika Borwa (Tswana) Rhandi ya Afrika-Dzonga (Tsonga) Rannda ya Afurika Tshipembe (Venda) ISO 4217Co...

Sexual abuse of young athletes by coaches and other adults from 1992–2016 USA Gymnastics logo The USA Gymnastics sex abuse scandal relates to the sexual abuse of hundreds of gymnasts—primarily minors—over two decades in the United States, starting in the 1990s. It is considered the largest sexual abuse scandal in sports history.[1][2][3][4] More than 500 athletes alleged that they were sexually assaulted by gym owners, coaches, and staff working for gymna...

Powervolley MilanoPallavolo Segni distintiviUniformi di gara Casa Trasferta Nome sponsorizzatoAllianz Milano Colori sociali Celeste e bianco Dati societariCittàMilano Nazione Italia ConfederazioneCEV FederazioneFIPAV CampionatoSuperlega Fondazione2010 Scioglimento2011 Rifondazione2012 Presidente Lucio Fusaro Allenatore Roberto Piazza ImpiantoPalaLido(5 347 posti) Sito webwww.powervolleymilano.it Palmarès Trofei internazionali1 Coppe CEV/Challenge Cup Si invita a seguire le diretti...

「THE」重定向至此。关于和THE同名的其他意思,请见「英语定冠词“The”」和「[[:THE]]」。 泰晤士高等教育2012年5月3日至9日的第2,048期主编Ann Mroz类别高等教育发行周期周刊首发日期1971年10月(初名《泰晤士高等教育增刊》)公司TSL Education Ltd.创刊地区英国语言英语网站http://www.timeshighereducation.co.uk/ISSN0049-3929 《泰晤士高等教育》(英文全称:Times Higher Education,英文�...

Pour l'album de la chanteuse Nâdiya sorti en 2004, voir 16/9 (album). Le format 16/9 (1,78:1), désigne un format d'image (proportions), et également les téléviseurs (dits télévisions) au « format large ». Dans ce format, la largeur de l'écran vaut les seize neuvièmes de sa hauteur. Il s’agit d’un format adopté sur le plan universal. La valeur 16/9 a été adoptée pour proposer un compromis utile lors de la télédiffusion de films de cinéma à la télé et s'adapt...

Model of electric multiple unit operated by the MTR Not to be confused with the now-retired MTR Metro Cammell EMU (AC) operated on the East Rail line by Kowloon-Canton Railway. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: MTR Metro Cammell EMU DC – news · newspapers · books · scholar · JSTOR (Februar...

Universitas MoliseUniversità degli Studi del Molisebahasa Latin: Universitas Studiorum Molisii Tampilkan peta yang diperbesarTampilkan peta yang diperkecil InformasiMotoKemajuan ilmiah untuk digunakan masyarakatJenisNegeriDidirikan1982RektorProf. Giovanni CannataJumlah mahasiswa8.095LokasiCampobasso, ItaliaTim olahragaCUS MoliseAfiliasiCinecaEUAUNIMEDSitus webunimol.it Universitas Molise (bahasa Italia: Università degli Studi del Molise), juga dikenal sebagai UNIMOL, i...

Decree issued by Tsar Nicholas II in 1899 The February Manifesto, also known as His Imperial Majesty's Graceful Announcement (decree collection 3/1899) was a legislative act given by Emperor of Russia Nicholas II on 15 February 1899, defining the legislation order of laws concerning the Grand Duchy of Finland. This included all laws which also concerned the interest of the Russian Empire. The manifesto left the Diet of Finland only an advisory role in passing these laws. The February Manifest...

Joseph HunterBorn(1783-02-06)6 February 1783Sheffield, EnglandDied9 May 1861(1861-05-09) (aged 78)London, England Joseph Hunter FSA (6 February 1783 – 9 May 1861) was a Unitarian Minister, antiquarian, and deputy keeper of public records now best known for his publications Hallamshire. The History and Topography of the Parish of Sheffield in the County of York, the two-volume South Yorkshire (a history of the Deanery of Doncaster), still considered among the best works written on the ...

Surian Toona ciliata Klasifikasi ilmiah Kerajaan: Plantae Klad: Tracheophyta Klad: Angiospermae Klad: Eudikotil Klad: Rosid Ordo: Sapindales Famili: Meliaceae Genus: Toona species Lihat teks. Untuk kegunaan lain, lihat Surian. Suren beralih ke halaman ini. Untuk kegunaan lain, lihat Suren (disambiguasi). Toona sinensis Surian atau suren adalah beberapa jenis tumbuhan anggota genus Toona, suku Meliaceae. Tumbuhan ini dikenal sebagai penghasil kayu berkualitas baik. Di alam ia ditemukan mulai ...

American baseball player (1884-1962) For other baseball people with similar names, see Robert Williams § Baseball. Baseball player Bob WilliamsCatcherBorn: (1884-04-27)April 27, 1884Monday, OhioDied: August 6, 1962(1962-08-06) (aged 78)Nelsonville, OhioBatted: RightThrew: RightMLB debutJuly 3, 1911, for the New York HighlandersLast MLB appearanceSeptember 30, 1913, for the New York YankeesMLB statisticsBatting average.164Home runs0hits11 Teams New York High...









