Нормований многочлен
|
Read other articles:

NBC Studios adalah dua fasilitas studio televisi yang dimiliki oleh National Broadcasting Company, dengan salah satunya berada di dalam GE Building di Rockefeller Center, New York City, dan satunya lagi di Burbank, California, di luar Los Angeles. Fasilitas produksi NBC ketiga, NBC Tower, terletak di Chicago, Illinois. Juga terdapat studio cadangan untuk kawasan New York di Marblehead, Massachusetts. NBC Studios juga dulunya merupakan nama bagi divisi produksi jaringan ini (sebelumnya NBC Pr...

Budi Widjanarko Waketbidminwa STIK Lemdiklat Polri Informasi pribadiLahir27 September 1966 (umur 57)JakartaAlma materAkademi Kepolisian (1995)Karier militerPihak IndonesiaDinas/cabang Kepolisian Negara Republik IndonesiaMasa dinas1989–2024Pangkat Brigadir Jenderal PolisiNRP66090438SatuanReserseSunting kotak info • L • B Brigjen. Pol. Budi Widjanarko, S.H., M.H. (lahir 27 September 1966) adalah seorang perwira tinggi Polri yang sejak 7 Desember 2023 menjabat seba...

Memorial in Brooklyn, New York, U.S. Not to be confused with Lafayette hillside memorial.Lafayette MemorialLafayette Memorial (2021)40°39′52″N 73°58′35.7″W / 40.66444°N 73.976583°W / 40.66444; -73.976583LocationProspect Park, Brooklyn, New York City, New York, United StatesDesignerDaniel Chester French (sculptor)Henry Bacon (architect)FabricatorGorham foundryPresbrey-Coykendall CompanyMaterialBronzeGraniteLength9 feet (2.7 m)Width22 feet (6.7 m)He...

Part of a series onBritish law Acts of Parliament of the United Kingdom Year 1801 1802 1803 1804 1805 1806 1807 1808 1809 1810 1811 1812 1813 1814 1815 1816 1817 1818 1819 1820 1821 1822 1823 1824 1825 1826 1827 1828 1829 1830 1831 1832 1833 1834 1835 1836 1837 1838 1839 1840 1841 1842 1843 1844 1845 1846 1847 1848 1849 1850 1851 1852 1853 1854 1855 1856 1857 1858 1859 1860 1861 1862 1863 1864 1865 1866 1867 1868 1869 1870 1871 1872 1873 1874 1875 1876 1877 1878 ...

Administrative entry restrictions Front cover of a Philippine passport. Visa requirements for Filipino citizens are administrative entry restrictions imposed on citizens of the Philippines by the authorities of other territories. As of February 9, 2024, Filipino citizens had visa-free or visa on arrival access to 69 countries and territories, ranking the Philippine passport 75th in the world according to the Henley Passport Index.[1] Visa requirements map Visa requirements for Filipin...

2009 European Parliament election in Romania ← 2007 7 June 2009 2014 → All 33 seats of Romania in the European ParliamentTurnout27.67% First party Second party Third party Leader Mircea Geoană Emil Boc Crin Antonescu Party PSD+PC PDL PNL Leader since 23 April 2005 15 December 2007 21 March 2009 Last election 10 seats 16 seats 6 seats Seats won 11 10 5 Seat change 1 6 1 Popular vote 1,504,218 1,438,000 702,974 Percentage 31.07% 29....

Lapangan Battery Park City South End Avenue Battery Park City adalah sebuah komunitas terencana seluas 92 are (0,4 km²) di ujung barat daya Lower Manhattan di New York City, Amerika Serikat. Tanah tempat berdirinya dibentuk di Sungai Hudson menggunakan 1,2 juta yard kubik (917.000 m3) tanah dan bebatuan yang dikeruk selama pembangunan World Trade Center dan proyek konstruksi lainnya, juga dari pasir yang dikeruk dari New York Harbor di lepas Staten Island.[1] Permukiman ini yang...

St Joseph's Abbey, StorringtonSt Joseph's Abbey (The Abbey), Storrington at Storrington in Sussex, England, was originally a rectory, later a small country house and then a convent school. St Joseph's Abbey, Storrington It is an irregular five bay, two and three storey house built in 1871-2 by the Rev. George Faithfull in the Victorian Gothic style, reusing material from the 1621 rectory which was demolished at this time.[1] In the 1880s it was the residence of Colonel Walter George ...

Флаг гордости бисексуалов Бисексуальность Сексуальные ориентации Бисексуальность Пансексуальность Полисексуальность Моносексуальность Сексуальные идентичности Би-любопытство Гетерогибкость и гомогибкость Сексуальная текучесть Исследования Шк...

Флаг гордости бисексуалов Бисексуальность Сексуальные ориентации Бисексуальность Пансексуальность Полисексуальность Моносексуальность Сексуальные идентичности Би-любопытство Гетерогибкость и гомогибкость Сексуальная текучесть Исследования Шк...

Autódromo Internacional de GuaporéGuaporé International RacewayVitacir Paludo Circuit (1976–present)LocationGuaporé, Rio Grande do Sul, BrazilTime zoneUTC-03:00Coordinates28°50′41″S 51°51′14″W / 28.84472°S 51.85389°W / -28.84472; -51.85389Capacity60,000OperatorAGA - Associação Guaporense de AutomobilismoOpened21 December 1969; 54 years ago (1969-12-21) (dirt track)17 October 1976; 47 years ago (1976-10-17) (aspha...

American college basketball season 2024–25 Georgetown Hoyas men's basketballConferenceBig EastRecord0–0 (0–0 Big East)Head coachEd Cooley (2nd season)Assistant coaches Jeff Battle Kenny Johnson[1][2][3][4] Brian Blaney Home arenaCapital One ArenaSeasons← 2023–242025–26 → 2024–25 Big East men's basketball standings vte Conf Overall Team W L PCT W L PCT Butler 0 – 0 – 0 –...
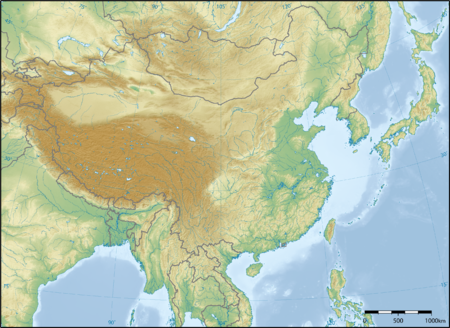
中华人民共和国位于东亚[1],领土陆地面积估约960万平方千米[2],人口超过14亿[3],是世界第二大经济体[4][5],是最大的出口国和第二大进口国[6][7]。中国是联合国安全理事会五个常任理事国之一和亚洲太平洋经济合作组织的常务会员。[8][9][10][11] 名称代码 中华人民共和国国旗中华人民共和国国徽 通用当地�...

Artikel ini memberikan informasi dasar tentang topik kesehatan. Informasi dalam artikel ini hanya boleh digunakan untuk penjelasan ilmiah; bukan untuk diagnosis diri dan tidak dapat menggantikan diagnosis medis. Wikipedia tidak memberikan konsultasi medis. Jika Anda perlu bantuan atau hendak berobat, berkonsultasilah dengan tenaga kesehatan profesional. MeningitisMeninges sistem saraf pusat: dura mater, arachnoid, dan pia mater.Informasi umumSpesialisasiNeurologi, penyakit menular Menin...

Sekolah Komando Kesatuan Angkatan Udara(Komando Pembinaan Doktrin, Pendidikan dan Latihan TNI Angkatan Udara)Dibentuk10 Januari 1966Negara IndonesiaCabang TNI Angkatan UdaraTipe unitKomando PendidikanBagian dari KodiklatauJulukanSekkauMotoVicaksana Sakti ViraSitus webwww.sekkau.mil.idTokohKomandanMarsekal Pertama TNI Sri Duto Dhanisworo, S.Ap., M.Si.Wadan- Sekolah Komando Kesatuan TNI Angkatan Udara (disingkat Sekkau) adalah satuan pelaksana Komando Pembinaan Doktrin, Pendidikan dan Lati...

American biographer, editor, essayist (born 1961) Stacy SchiffSchiff in 2016BornStacy Madeleine Schiff (1961-10-26) October 26, 1961 (age 62)Adams, MassachusettsOccupationWriter and editorEducationPhillips Academy (Andover)Alma materWilliams CollegeGenreBiography, essay, non-fictionNotable awardsPulitzer PrizeWebsitestacyschiff.com Stacy Madeleine Schiff (born October 26, 1961)[1] is an American former editor, essayist, and author of five biographies. Her biography of Véra ...

American alternative metal band For their self-titled studio album, see Deftones (album). DeftonesDeftones performing at the Shepherd's Bush Empire in 2011; from left to right: Carpenter, Cunningham, Moreno, and VegaBackground informationOriginSacramento, California, U.S.Genres Alternative metal art rock experimental rock shoegaze post-hardcore nu metal (early) DiscographyDeftones discographyYears active1988–presentLabels Maverick Warner Reprise Spinoffs Team Sleep Crosses Palms Phallucy So...

Park in Mohave County, Arizona Cattail Cove State ParkCattail Cove State Park, March 2015Location of Cattail Cove State Park in ArizonaLocationMohave, Arizona, United StatesCoordinates34°21′2″N 114°10′12″W / 34.35056°N 114.17000°W / 34.35056; -114.17000Area2,000 acres (8.1 km2)Established1970Visitors86,385 (in 2022)[1]Governing bodyArizona State Parks Cattail Cove State Park is a state park of Arizona, USA, on the shore of Lake Ha...

16th-century English legislature Part of a series on theHistory of the Church of EnglandWestminster Abbey (1749) by Canaletto Middle Ages (597–1500)Anglo-Saxon ChristianityReligion in Medieval EnglandConvocations of Canterbury and YorkDevelopment of dioceses Reformation (1509–1559)Reformation ParliamentDissolution of the MonasteriesThomas CranmerBook of Common Prayer (1549)Edwardine OrdinalsBook of Common Prayer (1552)Forty-two ArticlesMartyrsMarian exiles Elizabethan Church (1558–1603)...

Para otros usos de este término, véase Álava (desambiguación). ÁlavaAraba/Álava Provincia de EspañaBanderaEscudo Coordenadas 42°50′00″N 2°45′00″O / 42.833333333333, -2.75Capital VitoriaIdioma oficial Español y euskeraEntidad Provincia de España • País España España • Comunidad País Vasco País VascoCongresoSenadoParlamento VascoJuntas GeneralesDiputado general 4 diputados4 senadores25 parlamentariosautonómicos51 junteros/asprovi...










![{\displaystyle C:=\{b\in B:\exists \,p(x)\in A[x]\,,{\hbox{ що є нормованим і таким, що }}p(b)=0\}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d03be1eaa3ef053a5e0cad2976ebf7e656c3708a)









