–Ь–µ—В–Њ–і —И—В—А–∞—Д—Ц–≤
|
Read other articles:

Pemandangan udara Fasilitas Penahanan Parwan saat perampungannya pada 2009. Fasilitas Penahanan Parwan adalah penjara militer utama Afganistan. Berada di sebelah Pangkalan Udara Bagram, Provinsi Parwan, Afganistan, penjara tersebut dibangun oleh AS pada masa pemerintahan G.W. Bush. Merumahi kombatan lokal dan asing, Fasilitas Penahanan Parwan diurus oleh Tentara Nasional Afganistan. Pranala luar Wikimedia Commons memiliki media mengenai Parwan Detention Facility. Wikisumber memiliki naskah as...

ЎІўДЎІўЖЎ™ЎЃЎІЎ®ЎІЎ™ ЎІўДЎєЎІўЕЎ© ЎІўДўКЎІЎ®ЎІўЖўКЎ© 2021 ЎІўДўКЎІЎ®ЎІўЖ вЖТ 31 Ў£ўГЎ™ўИЎ®Ў± 2021 ЎєЎѓЎѓ ЎІўДўЖЎІЎЃЎ®ўКўЖ 105224103 [1] Ў•ЎђўЕЎІўДўК ЎІўДЎ£ЎµўИЎІЎ™ 58900259 [1] ЎєЎѓЎѓ ЎІўДЎ£ЎµўИЎІЎ™ ЎІўДўЕўВЎ®ўИўДЎ© 57457032 [1] ЎђЎ±Ў™ ЎІўДЎІўЖЎ™ЎЃЎІЎ®ЎІЎ™ ЎІўДЎєЎІўЕЎ© ўБўК ЎІўДўКЎІЎ®ЎІўЖ ўБўК 31 Ў£ўГЎ™ўИЎ®Ў± 2021ЎМ [2] ўИўБўВўЛЎІ ўДўЕЎІ ўКўВЎ™ЎґўКўЗ ЎѓЎ≥Ў™ўИЎ± ЎІўДўКЎІЎ®ЎІўЖ. ЎђЎ±ўК ЎІўДЎ™ЎµўИўКЎ™ ўБўК ЎђўЕўКЎє ЎѓўИЎІЎ¶Ў± пњљ...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Meme Muslim вАУ berita ¬Ј surat kabar ¬Ј buku ¬Ј cendekiawan ¬Ј JSTOR (December 2022) meme Muslim tentang Wikipedia dan ibadah (salat) Meme Muslim, meme Islam, atau meme halal adalah salah satu jenis meme Internet ...

Kedaulatan Westphalia adalah konsep kedaulatan negara bangsa di teritorinya sendiri tanpa campur tangan agen asing dalam struktur domestiknya. Para pakar hubungan internasional menyebut sistem internasional negara, perusahaan multinasional, dan organisasi modern yang berorientasi Barat bermula di Perdamaian Westphalia tahun 1648.[1] Baik dasar maupun kesimpulan pandangan ini dikritik oleh sejumlah[siapa?] akademisi dan politikus revisionis. Para revisionis mempertanyakan penti...

CH-148 Cyclone Un CH-148 de l'Aviation royale canadienne expos√© au Salon du Bourget en 2012. R√іle H√©licopt√®re maritime Constructeur Sikorsky Aircraft Premier vol 15 novembre 2008 Mise en service 2015 Date de retrait Toujours en service Investissement 7,6 milliards canadiens Nombre construit 18 livr√©s en mars 2020, 28 pr√©vus. √Йquipage 4 + 22 soldats Motorisation Moteur General Electric CT7-8A Nombre 2 Type Turbomoteurs Puissance unitaire 3 000 ch Nombre de pales 4 Dimensions ...

Airline of Taiwan Not to be confused with Ewa Air, EVAS Air, or Evergreen International Airlines. EVA Air йХЈж¶ЃиИ™з©Ї IATA ICAO Callsign BR EVA EVA Founded8 March 1989; 35 years ago (1989-03-08)Commenced operations1 July 1991; 32 years ago (1991-07-01)HubsTaipeiвАУTaoyuanFocus citiesBangkokвАУSuvarnabhumiKaohsiungTaipeiвАУSongshanFrequent-flyer programInfinity MileageLandsAllianceStar Alliance[1][2]SubsidiariesUNI AirFleet size85[3]...

Song by Jean Sibelius (1911) AriosoArt song by Jean SibeliusThe composer (c. 1911)Opus3TextFlickans årstider by Runeberg[1]LanguageSwedishComposed1911 (1911)PublisherApostol [fi] (1913; pf. version)[2]Westerlund [fi] (1951; str. version)[1]Duration4 mins.[3]PremiereDate18 September 1913 (1913-09-18)[2]LocationHelsinki, Grand Duchy of FinlandPerformersIda Ekman (soprano)Karl Ekman &...

Cet article est une √©bauche concernant une localit√© suisse. Vous pouvez partager vos connaissances en lвАЩam√©liorant (comment ?) selon les recommandations des projets correspondants. W√§denswil Vue sur W√§denswil et le lac de Zurich. Armoiries Administration Pays Suisse Canton Zurich District Horgen Localit√©(s) Au (de), H√Љtten, Sch√ґnenberg, W√§denswil, W√§denswiler Berg. Maire Philipp Kutter (Le Centre) NPA 8804 Au8820 W√§denswil8824 Sch√ґnenberg8825 H√Љtten No OFS 0293 ...

–°–µ–ї—М—Б–Ї–Њ–µ –њ–Њ—Б–µ–ї–µ–љ–Є–µ –†–Њ—Б—Б–Є–Є (–Ь–Ю 2-–≥–Њ —Г—А–Њ–≤–љ—П)–Э–Њ–≤–Њ—В–Є—В–∞—А–Њ–≤—Б–Ї–Њ–µ —Б–µ–ї—М—Б–Ї–Њ–µ –њ–Њ—Б–µ–ї–µ–љ–Є–µ –§–ї–∞–≥[d] –У–µ—А–± 45¬∞14вА≤09вА≥ —Б. —И. 38¬∞58вА≤16вА≥ –≤. –і.HG–ѓO –°—В—А–∞–љ–∞ –†–Њ—Б—Б–Є—П –°—Г–±—К–µ–Ї—В –†–§ –Ъ—А–∞—Б–љ–Њ–і–∞—А—Б–Ї–Є–є –Ї—А–∞–є –†–∞–є–Њ–љ –Ф–Є–љ—Б–Ї–Њ–є –Т–Ї–ї—О—З–∞–µ—В 4 –љ–∞—Б–µ–ї—С–љ–љ—Л—Е –њ—Г–љ–Ї—В–∞ –Р–і–Љ. —Ж–µ–љ—В—А –Э–Њ–≤–Њ—В–Є—В–∞—А–Њ–≤—Б–Ї–∞—П –У–ї–∞–≤–∞ —Б–µ–ї—М—Б–Ї–Њ–≥–Њ –њ–Њ—Бпњљ...

Cet article est une √©bauche concernant Internet et le Groenland. Vous pouvez partager vos connaissances en lвАЩam√©liorant (comment ?) selon les recommandations des projets correspondants. .gl D√©but 1994 Type Domaine national de premier niveau √Йtat Actif Registre TELE Greenland Parrain√© par TELE Greenland Pays Groenland Restrictions Aucune Structure Les noms peuvent enregistr√©s directement au deuxi√®me niveau Site Web http://www.nic.gl/ modifier .gl est le domaine de premier ...

–Ф–µ—А–ґ–∞–≤–љ–Є–є –Ї–Њ–Љ—Ц—В–µ—В —В–µ–ї–µ–±–∞—З–µ–љ–љ—П —Ц —А–∞–і—Ц–Њ–Љ–Њ–≤–ї–µ–љ–љ—П –£–Ї—А–∞—Ч–љ–Є (–Ф–µ—А–ґ–Ї–Њ–Љ—В–µ–ї–µ—А–∞–і—Ц–Њ) –Я—А–Є–Љ—Ц—Й–µ–љ–љ—П –Ї–Њ–Љ—Ц—В–µ—В—Г–Ч–∞–≥–∞–ї—М–љ–∞ —Ц–љ—Д–Њ—А–Љ–∞—Ж—Ц—П–Ъ—А–∞—Ч–љ–∞ –£–Ї—А–∞—Ч–љ–∞–Ф–∞—В–∞ —Б—В–≤–Њ—А–µ–љ–љ—П 2003–Ъ–µ—А—Ц–≤–љ–µ –≤—Ц–і–Њ–Љ—Б—В–≤–Њ –Ъ–∞–±—Ц–љ–µ—В –Ь—Ц–љ—Ц—Б—В—А—Ц–≤ –£–Ї—А–∞—Ч–љ–Є–†—Ц—З–љ–Є–є –±—О–і–ґ–µ—В 1 964 898 500 вВі[1]–У–Њ–ї–Њ–≤–∞ –Ю–ї–µ–≥ –Э–∞–ї–Є–≤–∞–є–Ї–Њ–Я—Ц–і–≤—Ц–і–Њ–Љ—З—Ц –Њ—А...

ињ™е••жЦѓиЊЊе§Ъ¬Јй©ђеН°еЄХеК†е∞ФDiosdado Pangan Macapagalзђђ9дїїиП≤еЊЛи≥УзЄљзµ±дїїжЬЯ1961еєі12жЬИ30жЧ•вАФ1965еєі12жЬИ30жЧ•еЙНдїїеН°жіЫжЦѓ¬ЈP¬ЈеК†и•њдЇЪзїІдїїиієињ™еНЧеЊЈ¬Јй©ђзІСжЦѓзђђ6дїїиП≤еЊЛи≥УеЙѓзЄљзµ±дїїжЬЯ1957еєі12жЬИ30жЧ•вАФ1961еєі12жЬИ30жЧ•еЙНдїїеН°жіЫжЦѓ¬ЈP¬ЈеК†и•њдЇЪзїІдїїдЉКжЫЉзЇље∞Ф¬Јдљ©иО±жЦѓ дЄ™дЇЇиµДжЦЩеЗЇзФЯ(1910-09-28)1910еєі9жЬИ28жЧ• зЊОе±ђиП≤еЊЛи≥Уй¶ђе∞ЉжЛЙйАЭдЄЦ1997еєі4жЬИ21жЧ•(1997ж≠≤вАФ04вАФ21)пЉИ86ж≠≤пЉЙ иП≤еЊЛи≥Уй¶ђеН°ињ™еҐУеЬ∞ иП≤еЊЛи≥Уй¶ђеН°ињ™йБФзЊ©еЄВиЛ±...

ж≠§жЭ°зЫЃеЇПи®АзЂ†иКВж≤°жЬЙеЕЕеИЖжАїзїУеЕ®жЦЗеЖЕеЃєи¶БзВєгАВ (2019еєі3жЬИ21жЧ•)иѓЈиАГиЩСжЙ©еЕЕеЇПи®АпЉМжЄЕжЩ∞ж¶Вињ∞жЭ°зЫЃжЙАжЬЙйЗНйїЮгАВиѓЈеЬ®жЭ°зЫЃзЪДиЃ®иЃЇй°µиЃ®иЃЇж≠§йЧЃйҐШгАВ еУИиР®еЕЛжЦѓеЭ¶зЄљзµ±еУИиЦ©еЕЛзЄљзµ±жЧЧзПЊдїї“Ъ–∞—Б—Л–Љ-–Ц–Њ–Љ–∞—А—В –Ъ–µ–Љ–µ–ї“±–ї—Л –Ґ–Њ“Ы–∞–µ–≤еН°зСЯеІЖиЛ•й©ђе∞ФзЙє¬ЈжЙШеН°иАґе§ЂиЗ™2019еєі3жЬИ20жЧ•еЬ®дїїдїїжЬЯ7еєій¶ЦдїїеК™е∞ФиЛПдЄє¬ЈзЇ≥жЙОе∞ФеЈіиАґе§ЂиЃЊзЂЛ1990еєі4жЬИ24жЧ•пЉИеУИиЦ©еЕЛиШЗзґ≠еЯГз§ЊжЬГдЄїзЊ©еЕ±еТМеЬЛзЄљзµ±пЉЙ еУИиР®еЕЛжЦѓеЭ¶ еУИиР®еЕЛжЦѓеЭ¶жФњеЇЬ...

Depiction of the Sun god of Heaven at the Hittite cliff sanctuary of Yazƒ±lƒ±kaya (At left, alongside the Moon god (Hurrian Ku≈°uбЄЂ, Hittite Arma) The Sun god of Heaven (Hittite: nepi≈°a≈° I≈°tanu[1]) was a Hittite solar deity. He was the second-most worshipped solar deity of the Hittites, after the Sun goddess of Arinna.[2] The Sun god of Heaven was identified with the Hurrian solar deity, ≈†imige.[3] From the time of TudбЄЂaliya III, the Sun god of Heaven was the pr...

Persem MojokertoNama lengkapPersatuan Sepakbola MojokertoJulukan Laskar Damarwulan Badai Biru Blue Force Berdiri26 Januari 1931StadionStadion Ahmad Yani Kota Mojokerto, Jawa Timur(Kapasitas: 10,000)PemilikYayasan Persem Mojokerto[1]KetuaArtian Yunianto[2]LigaLiga 3 Kostum kandang Persatuan Sepakbola Mojokerto atau PERSEM adalah klub sepak bola Indonesia yang berbasis di Kota Mojokerto, Jawa Timur. Klub ini dulu adalah bernama Modjokerto Voetbalbond (1920-1930). Setelah PSSI be...

Ethnic group Azerbaijanis in GermanyTotal population140,000-200,000 (census 2008)[citation needed]Regions with significant populationsBerlin, Cologne, Bremen, Hamburg, Mainz, Frankfurt am Main, Munich, D√Љsseldorf, StuttgartLanguagesAzerbaijani, German, Persian, Russian, Turkish,ReligionShia IslamRelated ethnic groupsturks in Germany Part of a series onAzerbaijanis Culture Architecture Art Cinema Cuisine Dance Dress Literature Media Music Folklore Religion Sport Theatre Tourism Tradi...

2015 American filmAll Hallows' Eve 2Release posterDirected byBryan NortonAntonio PadovanJay HolbenJames and Jon KondelikAndrés BorghiProduced byDamien LeoneJesse BagetStarringAndrea MonierDistributed byImage EntertainmentRelease date October 6, 2015 (2015-10-06) CountryUnited StatesLanguageEnglish All Hallows' Eve 2 is a 2015 American horror anthology film.[1] The film is a standalone sequel to All Hallows' Eve (2013).[2][3] The film was released on VOD...
Digital copy protection High-bandwidth Digital Content Protection (HDCP) is a form of digital copy protection developed by Intel Corporation[1] to prevent copying of digital audio and video content as it travels across connections. Types of connections include DisplayPort (DP), Digital Visual Interface (DVI), and High-Definition Multimedia Interface (HDMI), as well as less popular or now deprecated protocols like Gigabit Video Interface (GVIF) and Unified Display Interface (UDI). The ...

COVID-19 pandemicConfirmed deaths per 100,000 population,[1][note 1] as of 20 December 2023 555+ 100вАУ555 18вАУ100 3.3вАУ18 0.6вАУ3.3 0.1вАУ0.6 <0.1 No deaths or no dataDiseaseCOVID-19Virus strainSARS-CoV-2SourceProbably bats, possibly via pangolins[2][3][4]LocationWorldwideFirst outbreakChina[5]Index caseWuhan, Hubei, China30¬∞37вА≤11вА≥N 114¬∞15вА≤28пњљ...
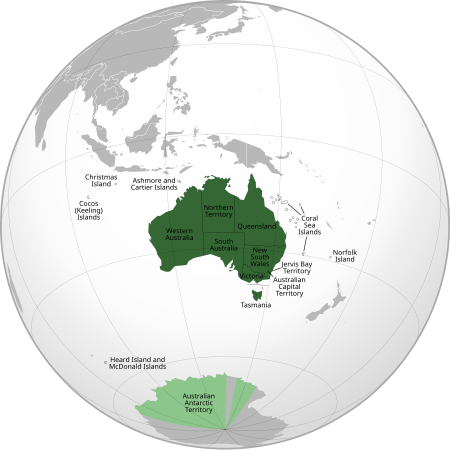
Animated map of the territorial evolution of Australia The first colonies of the British Empire on the continent of Australia were the penal colony of New South Wales, founded in 1788, and the Swan River Colony (later renamed Western Australia), founded in 1829. Over the next few decades, the colonies of New Zealand, Queensland, South Australia, Van Diemen's Land (later renamed Tasmania), and Victoria were created from New South Wales, as well as an aborted Colony of North Australia. On 1 Ja...





