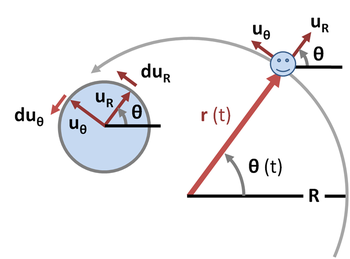
Коловий рух
|
Read other articles:

2008 live album by Sunny MurrayThe Gearbox Explodes!Live album by Sunny MurrayReleased2008RecordedOctober 24, 2006VenueSt. Dominics Retreat Working Mens Club, Newcastle upon Tyne, EnglandGenreFree jazzLabelFoghorn Records FOGCD009Sunny Murray chronology Perles Noires(2005) The Gearbox Explodes!(2008) Sonic Liberation Front Meets Sunny Murray(2010) The Gearbox Explodes! is a live album by drummer Sunny Murray. It was recorded in October 2006 at the St. Dominics Retreat Working Mens Clu...

Homongi (訪問着code: ja is deprecated , Hōmon-gi) adalah salah satu jenis kimono formal untuk wanita yang menikah atau belum menikah. Menurut urutan tingkat formalitas, homongi berada setingkat di bawah irotomesode. Wanita Jepang memakai Homongi Dikenakan bersama fukuro obi, homongi dipakai sewaktu diundang ke pesta pernikahan yang bukan diadakan sanak keluarga, upacara minum teh, merayakan tahun baru, dan pesta-pesta.[1] Sewaktu membeli kimono, pemakai bisa memesan lebar lengan k...

Artikel ini membahas mengenai narkotika, psikotropika, dan zat adiktif lainnya. Informasi mengenai zat dan obat-obatan terlarang hanya dimuat demi kepentingan ilmu pengetahuan. Kepemilikan dan pengedaran narkoba adalah tindakan melanggar hukum di berbagai negara. Baca: penyangkalan umum lihat pula: nasihat untuk orang tua. Cannabis Periode Miosen Awal - Sekarang 19.6–0 jtyl PreЄ Є O S D C P T J K Pg N Hennep TumbuhanJenis buahBuah kurung TaksonomiDivisiTracheophytaSubdivisiSperm...

Account of the universe and its laws by the ancient North Germanic peoples A depiction of the personified moon, Máni, and the personified Sun, Sól by Lorenz Frølich, 1795 Norse cosmology is the account of the universe and its laws by the ancient North Germanic peoples. The topic encompasses concepts from Norse mythology, such as notations of time and space, cosmogony, personifications, anthropogeny, and eschatology. Like other aspects of Norse mythology, these concepts are primarily record...

Zakharia 13Sebagian Kitab Zakharia pada Codex Gigas, yang dibuat sekitar abad ke-13.KitabKitab ZakhariaKategoriNabi-nabi KecilBagian Alkitab KristenPerjanjian LamaUrutan dalamKitab Kristen38← pasal 12 pasal 14 → Zakharia 13 (disingkat Zak 13) adalah bagian dari Kitab Zakharia dalam Alkitab Ibrani dan Perjanjian Lama di Alkitab Kristen. Memuat Firman Allah yang disampaikan dengan perantaraan nabi Zakharia.[1][2] Teks Naskah aslinya ditulis dalam bahasa Ibrani. Pasal...

War fought by some Greek city-states and Ptolemaic Egypt against Antigonid Macedonian This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Chremonidean War – news · newspapers · books · scholar · JSTOR (January 2022) (Learn how and when to remove this template message) Chremonidean WarDate267–261 BCLocationGree...

Questa voce o sezione sull'argomento attori britannici non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Frances Fisher nel 2014 Frances Louise Fisher (Milford-on-Sea, 11 maggio 1952) è un'attrice statunitense. Indice 1 Biografia 1.1 Vita privata 2 Filmografia 2.1 Cinema 2.2 Televisione 3 Doppiatrici itali...

Species of annelid worm Alvinella pompejana Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Annelida Clade: Pleistoannelida Clade: Sedentaria Order: Terebellida Family: Alvinellidae Genus: Alvinella Species: A. pompejana Binomial name Alvinella pompejanaDesbruyères and Laubier, 1980 Alvinella pompejana, the Pompeii worm, is a species of deep-sea polychaete worm (commonly referred to as bristle worms). It is an extremophile found only at hydrothermal vents in the Pa...

Region in Pennsylvania Autumn on a small road in Somerset County The Laurel Highlands is a region in southwestern Pennsylvania made up of Fayette County, Somerset County, and Westmoreland County.[1] It has a population of about 600,000 people. The region is approximately fifty-five miles southeast of Pittsburgh; the Laurel Highlands center on Laurel Hill and Chestnut Ridge of the Allegheny Mountains. The mountains making up the Laurel Highlands are the highest in Pennsylvania, with Mo...

John-Laffnie de Jager Nazionalità Sudafrica Altezza 193 cm Peso 82 kg Tennis Carriera Singolare1 Vittorie/sconfitte 0-3 Titoli vinti 0 Miglior ranking 313º (12 ottobre 1992) Risultati nei tornei del Grande Slam Australian Open Roland Garros Wimbledon 1T (1992) US Open Doppio1 Vittorie/sconfitte 246-258 Titoli vinti 7 Miglior ranking 11º (31 luglio 2000) Risultati nei tornei del Grande Slam Australian Open SF (1993) Roland Garros 2T (1993, 1998) &#...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Public secondary magnet school in Chicago, Illinois, United StatesVon Steuben Metropolitan High SchoolAddress5039 N. Kimball AvenueChicago, Illinois 60625United StatesCoordinates41°58′24″N 87°42′48″W / 41.9732°N 87.7132°W / 41.9732; -87.7132InformationSchool typePublic Secondary MagnetMottoTogether, we are Von strong.Opened1930; 94 years ago (1930)School districtChicago Public SchoolsPrincipalJennifer SuttonGrades9–12GenderCoedEnrollment...

SMK Jenis Tank berat Negara asal Uni Soviet Sejarah pemakaian Masa penggunaan 1939 (purwarupa) Digunakan oleh Uni Soviet Pada perang Perang Musim Dingin Sejarah produksi Produsen Kirov Plant Diproduksi 1939 Jumlah produksi 1 Spesifikasi Berat 55 t (54 ton panjang) Panjang 8,75 m (28 ft 8 in) Lebar 3,36 m (11 ft 0 in) Tinggi 3,35 m (11 ft 0 in) Awak 7 Perisai 20-60 mm Senjatautama Meriam 45 mm M1932 (turet depan),...

Основная статья: Интегральная схема Идею интеграции множества стандартных электронных компонентов в монолитном кристалле полупроводника впервые предложил в 1952 году британский радиотехник Джеффри Даммер[англ.]. Год спустя Харвик Джонсон подал первую в истории патентн�...

School program for children before kindergarten The examples and perspective in this article may not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (February 2021) (Learn how and when to remove this message) A pre-kindergarten playground Childcare At home Parents Extended family Au pair Babysitter Governess Nanny Outside the home Daycare Pre-school playgroup Educational settings Early childh...

County in North Dakota, United States County in North DakotaGrand Forks CountyCountyGrand Forks County CourthouseLocation within the U.S. state of North DakotaNorth Dakota's location within the U.S.Coordinates: 47°55′N 97°27′W / 47.92°N 97.45°W / 47.92; -97.45Country United StatesState North DakotaFoundedJanuary 4, 1873 (created)March 2, 1875 (organized)SeatGrand ForksLargest cityGrand ForksArea • Total1,440 sq mi (3,700 km2...

List of events ← 1838 1837 1836 1839 in the United States → 1840 1841 1842 Decades: 1810s 1820s 1830s 1840s 1850s See also: History of the United States (1789–1849) Timeline of United States history (1820–1859) List of years in the United States 1839 in the United States1839 in U.S. states States Alabama Arkansas Connecticut Delaware Georgia Illinois Indiana Kentucky Louisiana Maine Maryland Massachusetts Michigan Mississippi Missouri New Hampshire New Jersey New York North Ca...

Cet article est une ébauche concernant le Gard. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Pour les articles homonymes, voir Avignon. Chemin-bas d'AvignonGéographiePays FranceAncien canton français canton de Nîmes-6Ancien canton français canton de Nîmes-5Ancien canton français canton de La VistrenqueArrondissement français arrondissement de NîmesCommune française NîmesCoordonnées 43° ...

Rugby union in New CaledoniaCountryNew CaledoniaGoverning bodyFrench Rugby Federation Comité Régional de Rugby de Nouvelle CalédonieNational team(s)New CaledoniaFirst playedlate 19th century Rugby union in New Caledonia is a minor but growing sport. Governing body The Comité Régional de Rugby de Nouvelle Calédonie is a committee under the umbrella of the French Rugby Federation which is the governing body for rugby union within New Caledonia.[1] The committee is not affiliated ...