Задача Коші
|
Read other articles:

BanjaranKelurahanNegara IndonesiaProvinsiJawa TimurKotaKediriKecamatanKotaKode Kemendagri35.71.02.1012 Kode BPS3571020012 Luas... km²Jumlah penduduk... jiwaKepadatan... jiwa/km² Untuk tempat lain yang bernama sama, lihat Banjaran. Banjaran adalah sebuah kelurahan di wilayah Kecamatan Kota, Kota Kediri, Provinsi Jawa Timur. Kelurahan Banjaran terdiri dari 49 Rukun Tetangga (RT), 10 Rukun Warga (RW). Kelurahan Banjaran memiliki banyak potensi yang bisa dikembangkan dan memberikan dampak ...

بورت لافاكا الإحداثيات 28°26′56″N 96°37′47″W / 28.448888888889°N 96.629722222222°W / 28.448888888889; -96.629722222222 [1] تقسيم إداري البلد الولايات المتحدة[2][3] التقسيم الأعلى مقاطعة كالهاون عاصمة لـ مقاطعة كالهاون خصائص جغرافية المساحة 36.535087 كيلومتر مرب...

Questa voce o sezione sull'argomento storia di famiglia non cita le fonti necessarie o quelle presenti sono insufficienti. Commento: l'unica nota si riferisce ad un argomento marginale rispetto alla voce Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Questa voce o sezione sull'argomento storia di famiglia è ritenuta da controllare. Motivo: la voce si intitola duch...

The Right HonourableEmmerson Dambudzo Mnangagwa Presiden Zimbabwe ke-3PetahanaMulai menjabat 24 November 2017Wakil PresidenPhelekezela Mphoko PendahuluRobert MugabePenggantiPetahanaPresiden dan Sekretaris Pertama ZANU-PFPetahanaMulai menjabat 19 November 2017Ketua NasionalSimon Khaya-Moyo PendahuluRobert MugabePenggantiPetahanaWakil Presiden Pertama ZimbabweMasa jabatan12 December 2014 – 6 November 2017PresidenRobert Mugabe PendahuluJoice MujuruPenggantiPhelekezela Mphoko I...

Katchal adalah pulau di Kepulauan Nikobar, India. Pulau ini memiliki luas sebesar 174.4 km². Pulau ini terletak 1600 km dari daratan India dan 305 km dari Port Blair. Katchal awalnya disebut Tihnyu. Referensi http://police.and.nic.in/katchal.htm Diarsipkan 2009-04-09 di Wayback Machine. http://www.and.nic.in/shelterP/katchalmap.htm http://tourism.andaman.nic.in/tourop.htm Diarsipkan 2012-04-22 di Wayback Machine. http://books.google.co.in/books?id=Fk8FQa2ZSFQC&pg=PA1018&am...

Podium di Olimpiade Musim Dingin 2010. Peraih medali seluncur indah tunggal putri: Mao Asada (kiri, perak), Yuna Kim (tengah, emas), Joannie Rochette (kanan, perunggu).Seorang konduktor orkestra berdiri di atas podium, sehingga dia dapat melihat dan dilihat oleh para musisi. Podium (atau Podia) adalah sebuah platform yang digunakan untuk mengangkat sesuatu ke atas lingkungannya. Kata ini berasal dari bahasa Yunani, πόδι (kaki). Dalam arsitektur, bangunan bisa diletakkan di atas podium bes...

Wanda-Zhonghe-Shulin Line's under-construction MRT Station Taipei Botanical Garden植物園Chinese nameTraditional Chinese植物園Simplified Chinese植物园TranscriptionsStandard MandarinHanyu PinyinZhíwùyuánBopomofoㄓˊㄨˋㄩㄢˊ General informationLocationNo. 53 Nanhai Rd.Zhongzheng, TaipeiTaiwanOperated by Taipei Rapid Transit System Line(s) Wanda–Zhonghe–Shulin Line (LG02) ConstructionStructure typeUndergroundOther informationStation codeLG02HistoryOpeningDecember 2025 (...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Historic house in Washington, D.C., United States This article is about the house in Washington, District of Columbia. For the Forrest House in St. Julian's, Malta, see Spinola Palace (St. Julian's). United States historic placeForrest-Marbury HouseU.S. National Register of Historic PlacesD.C. Inventory of Historic Sites Forrest-Marbury House, now the Embassy of Ukraine, in Georgetown, Washington, D.C.Location3350 M St., NW., Washington, D.C.Coordinates38°54′17″N 77°4′4″W / ...

Football tournament season 2013–14 Cypriot Cup for lower divisionsTournament detailsCountry CyprusDates30 October 2013 – 6 April 2014Teams18Final positionsChampionsAdonis(1st title)Runner-upElpida X.← 2012–132014–15 → The 2013–14 Cypriot Cup for lower divisions was the 6th edition of the Cypriot Cup for lower divisions. A total of 18 clubs entered the competition. It began on 30 October 2012 with the first round and concluded on 6 April 2014 with the final...

American politician (1890–1969) Pappy O'Daniel redirects here. For the fictional character of the same name, see O Brother, Where Art Thou? Not to be confused with William L. O'Daniel. W. Lee O'DanielO'Daniel c. 1938United States Senatorfrom TexasIn officeAugust 4, 1941 – January 3, 1949Preceded byAndrew Jackson HoustonSucceeded byLyndon B. Johnson34th Governor of TexasIn officeJanuary 17, 1939 – August 4, 1941LieutenantCoke R. StevensonPreceded byJames V...

Smelt Sands State Recreation SiteFishing at Smelt SandsShow map of OregonShow map of the United StatesTypePublic, stateLocationYachats, Lincoln County, OregonCoordinates44°19′19″N 124°06′21″W / 44.32203°N 124.10574°W / 44.32203; -124.10574Operated byOregon Parks and Recreation Department Smelt Sands State Recreation Site is a state park in the U.S. state of Oregon, administered by the Oregon Parks and Recreation Department. See also List of Oregon sta...
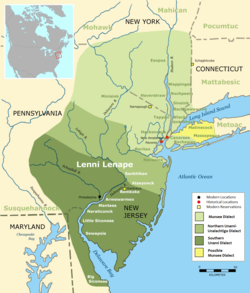
Native American people Ethnic group NanticokeTotal populationApproximately 1,200 in 16001,000 (1990)[1]Regions with significant populationsUnited States (Delaware, New Jersey, Maryland, Oklahoma), Canada (Ontario)[1]LanguagesEnglish, formerly Nanticoke languageReligionNative American religion, ChristianityRelated ethnic groupsAssateague, Choptank, Conoy, Patuxent, Piscataway, Pocomoke[1] Nanticoke River Delaware Indians The Nanticoke people are a Native American Algonq...

Veselin TopalovNama lengkapVeselin Topalov(Веселин Топалов)Asal negara BulgariaGelarGrandmasterJuara Dunia2005-2006 (FIDE)Rating FIDE2752(No. 12 on the May 2012 FIDE ratings list)Rating tertinggi2813 (Oktober 2006) Veselin Topalov (Bahasa Bulgaria: Веселин Топалов; lahir 15 Maret 1975) adalah pecatur berkebangsaan Bulgaria dan mantan juara dunia FIDE. Ia memenangi Kejuaraan Dunia Catur FIDE pada tahun 2005. Topalov mendapatkan pengharg...

Piala Winners UEFA 1996–1997Jadwalpenyelenggaraan1996 s.d. 1997Hasil turnamenJuara Barcelona (gelar ke-4)Tempat kedua Paris Saint-Germain← 1995–1996 1997–1998 → Piala Winners UEFA 1996–1997 adalah edisi ke-37 dari penyelenggaraan Piala Winners UEFA, turnamen sepak bola yang diikuti oleh pemenang kompetisi sistem piala di negara anggota UEFA. Edisi ini dimenangkan oleh tim Spanyol Barcelona setelah mengalahkan tim Prancis Paris Saint-Germain pada pertandingan final di De Ku...
List of events ← 1713 1712 1711 1710 1709 1714 in Ireland → 1715 1716 1717 1718 1719 Centuries: 16th 17th 18th 19th 20th Decades: 1690s 1700s 1710s 1720s 1730s See also:Other events of 1714 List of years in Ireland Events from the year 1714 in Ireland. Incumbent Monarch: Anne (until 1 August), then George I Events 1 August George I becomes King of Great Britain and Ireland upon the death of Anne. Former Governor of Londonderry and hero of the siege of Derry, Colonel John Mitchelbu...
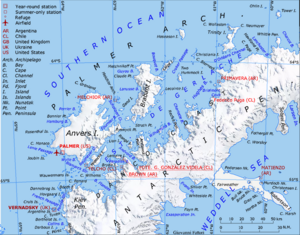
Antarctic baseVidela StationAntarctic baseGonzález Videla StationAntarctic Research Station Gonzales Videla located in Paradise BayVidela StationLocation of Videla Station in AntarcticaCoordinates: 64°49′26″S 62°51′25″W / 64.823954°S 62.857077°W / -64.823954; -62.857077Country ChileLocation in AntarcticaWaterboat PointGraham LandAdministered byInstituto Antártico ChilenoEstablished12 March 1951 (1951-03-12)Named forGabriel González Vi...
التحفيز الكهربائي للعصب عبر الجلد جهاز تحفيز كهربائي للعصب عبر الجلد. معلومات عامة من أنواع علاج تعديل مصدري - تعديل التحفيز الكهربائي للعصب عبر الجلد (بالإنجليزية: Transcutaneous electrical nerve stimulation) هو استخدام التيار الكهربائي الناتج عن جهاز لتحفيز الأعصاب لأغراض علاجية. �...

Ancient Celtic peoples of the Iberian Peninsula Ethnology of the Iberian Peninsula c. 200 BC, based on the map by Portuguese archeologist Luís Fraga da Silva [Wikidata] The Celtiberians were a group of Celts and Celticized peoples inhabiting an area in the central-northeastern Iberian Peninsula during the final centuries BC. They were explicitly mentioned as being Celts by several classic authors (e.g. Strabo[1]). These tribes spoke the Celtiberian language and wrote it ...

1926 film Jean ChouanPromotional posterDirected byLuitz-MoratWritten byArthur BernèdeStarringRené NavarreMarthe ChaumontMaurice LagrenéeCinematographyFrank Daniau-JohnstonGeorges DaretHenri StuckertProductioncompanySociété des CinéromansDistributed byPathé Consortium CinémaRelease date 22 January 1926 (1926-01-22) Running time412 minCountryFranceLanguagesSilent French intertitles Jean Chouan is a 1926 French silent historical film directed by Luitz-Morat and starring Re...










