Джордан Чайлз

Джордан Чайлз
Jordan Chiles
Загальна інформація
ГромадянствоСША США
Народження15 квітня 2001(2001-04-15) (23 роки)
Туолетін, Орегон, США
Alma materКаліфорнійський університет в Лос-Анджелесі[1] і Prairie High Schoold
Вебсторінкаgym-style.com/jordanchiles/
Спорт
КраїнаСША США
Вид спортуСпортивна гімнастика
ТренериЛоран Ланді, Сісіл Ланді
Нагороди
Представник США США
спортивна гімнастика
Олімпійські ігри
Золото Париж 2024 командна першість
Срібло Токіо 2020 командна першість
Бронза Париж 2024 вільні вправи
Чемпіонат світу
Золото Ліверпуль 2022 командна першість
Срібло Ліверпуль 2022 опорний стрибок
Срібло Ліверпуль 2022 вільні вправи
Тихоокеанський чемпіонат
Золото Медельїн 2018 командна першість
Золото Медельїн 2018 опорний стрибок
Золото Медельїн 2018 вільні вправи
Бронза Медельїн 2018 колода
CMNS: Джордан Чайлз у Вікісховищі

Джордан Чайлз (англ. Jordan Chiles; нар. 15 квітня 2001, Туолетін, Орегон, США) — американська гімнастка. Срібна призерка Олімпійських ігор у Токіо, Японія, у командній першості.

Біографія

Народилась у багатодітній родині, де, крім Джордан, виховуються Ясмін, Джейд, Таймен і Тайрус.[2]

Після школи продовжить навчання в університеті Каліфорнії. На олімпійський сезон взяла академічну відпустку.

Мала пропозиції спонсорського контракту, але вирішила відмовитись від статусу професіонала, щоб мати змогу виступати в студентській лізі.[3]

Спортивна кар'єра

Відвели до секції спортивної гімнастики через непосидючість, постійне виконання колеса та ходіння на руках.

2017

Дебютувала в дорослій збірній США.

Після другого місця в багатоборстві на чемпіонаті США до складу збірної на чемпіонат світу в Монреалі, Канада, не потрапила.

2018

За результатами чемпіонату США та відбіркового турніру на чемпіонат світу в Досі, Катар, до складу збірної США на головний турнір року знов не відібралась. Після другої поспіль поразки за право представляти США на світовій першості наважилась на переїзд за 3000 км від рідного міста до Спрінга, Техас, для тренування в одній групі зі Сімоною Байлс.[4]

2019

Попри конкуренцію з найкращою гімнасткою сьогодення та значне зростання майстерності, потрапити до складу збірної на передолімпійський чемпіонат світу знов не вдалось.

У жовтні отримала травму зап'ястя, була прооперована. Одужання затягнулось до 10 тижнів. Відновитися вдалось швидко, але вправа на різновисоких брусах не підкорювалась. Коли надія на олімпійську збірну майже згасла, через пандемію коронавірусу Олімпійські ігри в Токіо, Японія, було перенесено на рік, що дало змогу Джордан повністю відновитися від травми та з новими силами штурмувати відбір на головний старт чотириріччя.[4]

2021

Олімпійський сезон почала з впевненої перемоги на Зимовому кубку в багатоборстві, опорному стрибку та вільних вправах, а також другої позиції на колоді.

На Американській класиці вдалось підтвердити високий рівень готовності, посівши друге місце в багатоборстві після Сімони Байлс.

На чемпіонаті США та олімпійському випробовуванні в багатоборстві за сумою двох днів продемонструвала треті результати, що не дало автоматично відібратися до олімпійської команди. Рішенням тренерського штабу була оголошена членом збірної США на Олімпійські ігри в Токіо, Японія, у командній першості.

На Олімпійських іграх в Токіо, Японія, у фіналі командної першості після невдалого виконання стрибка та вимушеного зняття Сімони Байлс Джордан замість опорного стрибка та вільних вправ вимушена була виконувати усі чотири вправи, при чому на різновисоких брусах вдалось набрати 14,166 балів, на колоді — 13,433 бали, а у вільних вправах на третій діагоналі впала, отримавши лиш 11,700 балів. Таким чином, спільно з Сімоною Байлс, Сунісою Лі та Грейс Мак-Калум набрали 166,096 балів та посіли друге місце, вперше з 2010 року програвши ОІ чи чемпіонати світу.[5]

2024

На Олімпійських іграх в Парижі, Франція, здобула командну перемогу в першості разом з Сімоною Байлс, Сунісою Лі, Джейд Кері та Гезлі Ріверою. В єдиному особистому фіналі ОІ - вільних вправах - виступала останньою. Після отримання оцінки в 13,666 балів та п'ятого місця подала протест на оцінку за складність, після перегляду якого оцінка була збільшена на 0,1 бала до 13,766 балів, що принесло спортсменці бронзову нагороду. Однак федерація Румунії подала позов до Спортивного арбітражного суду щодо подачі протесту американською збірною не протягом відведеної 1 хвилини після виставлення оцінки останній гімнастці, а через 1 хвилину 4 секунди, що призводить до анулювання протесту. Після розгляду скарги Спортивний арбітражний суд через 5 діб після нагородження задовольнив вимоги федерації гімнастики Румунії та постановив позбавити бронзової нагороди Джордан Чайлз та нагородити румунку Ану Барбосу.[6] Федерація США звернулась до Міжнародного олімпійського комітету щодо видачі другої бронзової нагороди Джордан Чайлз, посилаючись на прецедент на ОІ в Солт-Лейк-Сіті, США, однак отримала відмову.[7]

Результати на турнірах

Рік Змагання КБ ІБ Опорний стрибок Різновисокі бруси Колода Вільні вправи
2017 Чемпіонат США 2 7 4 8
2018 Кубок світу. Штутгарт 3
Тихоокеанський чемпіонат 1 1 3 1
Американська класика 8 2 8 6
Чемпіонат США 2
Табір відбору на чемпіонат світу 7
2019 Американська класика 8
Чемпіонат США 6 7 7
2021 Зимовий кубок[8] 1 1 4 2 1
Американська класика 2 2 4 2
Чемпіонат США[9] 3 3 4 4 4
Олімпійське випробовування[10] 3 2 4 3
Олімпійські ігри 2
2022 Чемпіонат NCAA 52
Чемпіонат США 3 3 4 3
Кубок виклику в Парижі 2 5 1
Чемпіонат світу 1 2 2
2024 Олімпійські ігри 1 3 5

Примітки

  1. ↑ https://www.teamusa.org/Athletes/CH/Jordan-Chiles
  2. ↑ USA Gymnastics | Jordan Chiles. usagym.org. Архів оригіналу за 2 липня 2021. Процитовано 8 липня 2021.
  3. ↑ CHILES Jordan - FIG Athlete Profile. www.gymnastics.sport. Архів оригіналу за 25 травня 2021. Процитовано 8 липня 2021.
  4. ↑ а б May 31; Championships, 2021 | 2021 US; News, 2021 US Championships-; Features; News; Features | (31 травня 2021). All Eyes On Chiles. Inside Gymnastics Magazine (англ.). Архів оригіналу за 9 липня 2021. Процитовано 8 липня 2021.
  5. ↑ Armour, Nancy. US women's gymnastics team claims silver in team final after Simone Biles withdraws at Tokyo Olympics. USA TODAY (амер.). Архів оригіналу за 27 липня 2021. Процитовано 27 липня 2021.
  6. ↑ Romania’s Ana Barbosu officially an Olympic floor bronze medalist. International Gymnast Magazine Online (амер.). 11 серпня 2024. Процитовано 11 серпня 2024.
  7. ↑ Brennan, Christine. In Jordan Chiles' case, IOC has precedent to hand out two bronze medals. USA TODAY (амер.). Процитовано 11 серпня 2024.
  8. ↑ 2021 Winter Cup - Women (PDF). Архів оригіналу (PDF) за 28 лютого 2021. Процитовано 28.02.2021.
  9. ↑ MyUSAGym. myusagym.com. Архів оригіналу за 8 червня 2021. Процитовано 8 липня 2021.
  10. ↑ MyUSAGym. myusagym.com. Архів оригіналу за 9 липня 2021. Процитовано 8 липня 2021.

Read other articles:

Suku Isakhar

Sketsa dari Portugis untuk Isakhar. Suku Isakhar (bahasa Ibrani: שבט יִשָּׂשׁכָר, Modern Shevet Yissakhar Tiberias Šḗḇeṭ Yiśśâḵār; Inggris: Tribe of Issacharcode: en is deprecated ) adalah salah satu dari suku-suku Israel menurut Alkitab Ibrani, keturunan dari Isakhar, anak Yakub. Pembagian tanah suku-suku Israel Wilayah Suku Isakhar menerima daerah kepunyaan mereka berdasarkan undian ke-4 pada zaman Yosua. Daerah mereka ialah Yizreel, Kesulot, Sunem, Hafa...

 

Человек прямоходящий

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

 

Toys (film)

1992 American film by Barry Levinson ToysTheatrical release posterDirected byBarry LevinsonWritten by Valerie Curtin Barry Levinson Produced by Mark Johnson Barry Levinson Starring Robin Williams Michael Gambon Joan Cusack Robin Wright LL Cool J CinematographyAdam GreenbergEdited byStu LinderMusic by Hans Zimmer Trevor Horn ProductioncompanyBaltimore PicturesDistributed by20th Century FoxRelease date December 18, 1992 (1992-12-18) Running time122 minutes[1]CountryUnited...

Robertson Davies

Canadian novelist Robertson DaviesCC OOnt FRSL FRSCDavies in 1982Born(1913-08-28)28 August 1913Thamesville, Ontario, CanadaDied2 December 1995(1995-12-02) (aged 82)Orangeville, Ontario, CanadaOccupationJournalist, playwright, professor, critic, novelistNationalityCanadianAlma materQueen's University (did not graduate) Balliol College, OxfordGenreNovels, plays, essays and reviewsNotable worksThe Deptford Trilogy, The Cornish Trilogy, The Salterton TrilogySpouseBrenda Ethe...

 

Jarigan

This Form of folk song based on Bengali festival of Muharram needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this Form of folk song based on Bengali festival of Muharram. Unsourced material may be challenged and removed.Find sources: Jarigan – news · newspapers · books · scholar · JSTOR (September 2019) (Learn how and when to remove this message) Baul, the mystic minstrel of B...

 

Béarn

Iparralde (sebelah kiri) dan Béarn (sebelah kanan) Béarn (US /beɪˈɑːrn/;[1][2] bahasa Prancis: [beaʁn]; bahasa Ositan: Bearn [beˈaɾ] atau Biarn; bahasa Basque: Bearno atau Biarno; bahasa Latin: Benearnia atau Bearnia) adalah salah satu provinsi tradisional Prancis, terletak di pegunungan Pirenia dan di dataran kaki mereka, di barat daya Prancis. Bersama dengan tiga provinsi Basque Soule, Navarra Hilir, dan Labourd, kepangeranan Bidache, serta sebagian...

G7611 Duyun–Shangri-La Expressway

Road in China Duyun–Shangri-La Expressway都匀－香格里拉高速公路Duxiang Expressway都香高速公路Route informationAuxiliary route of G76Major junctionsWest endShangri-La, YunnanEast endDuyun, Qiannan Buyei and Miao, Guizhou LocationCountryChina Highway system National Trunk Highway System Primary Auxiliary National Highways Transport in China ← G76→ G7612 The G7611 Duyun–Shangri-La Expressway (Chinese: 都匀—香格里拉高速公路), also referred to as ...

 

Ministry of Internal Affairs (Ukraine)

Ukrainian government ministry Ministry of Internal AffairsМіністерство внутрішніх справEmblem of the ministryBanner of the ministryMinistry overviewFormed22 January 1918 (106 years ago) (1918-01-22)Preceding agenciesMinistry of Internal Affair of UNR (1918-1920)State Secretariat of Internal Affairs of wUNR (1918-1919)Ministry (People's Commissariat) of Internal Affairs of UkrSSR (1918-1991)JurisdictionUkraineHeadquarters10 Akademika Bohomoltsia Street,...

 

Barbarian kingdoms

Kingdoms established by barbarian tribes in the former Western Roman Empire For the barbarian kingdoms in ancient China, see Five Barbarians. Political map of Europe, North Africa and the Middle East in 476, showing the remaining Eastern Roman Empire in the Eastern Mediterranean and the various new kingdoms in the territory of the former Western Roman EmpireThe barbarian kingdoms[1][2][3] were states founded by various non-Roman, primarily Germanic, peoples in Western ...

Killing of Alvin Cole

2020 police killing of a black teenager Killing of Alvin ColeTracey Cole speaks at a rally for her son on October 15, 2020, in Wauwatosa's Hart Park.DateFebruary 2, 2020; 4 years ago (2020-02-02)LocationWauwatosa, Wisconsin, U.S.TypePolice killing by shootingParticipantsJoseph Mensah (shooter)DeathsAlvin ColeChargesNone On the evening of February 2, 2020, Alvin Cole, a 17-year-old black male, was fatally shot by a Wauwatosa, Wisconsin black male police officer Joseph Mensah,...

 

Sovereign (koin Britania)

SovereignBritania RayaNilai1 pound sterlingMassa7,98805 gDiameter22,05 mmKetebalan1,52 mmTepiBergerigi (beberapa tidak dimaksudkan untuk sirkulasi memiliki tepi polos)Komposisi0,917 emas, 0,083 tembaga atau logam lainnyaEmas0,2354 ons troyTahun pencetakan1817–sekarangTanda cetakBeraneka. Ditemukan pada sisi belakang pada exergue antara desain dan tanggal terdapat Santo Georgius dan para penguasa Naga, dan di bawah bumban untuk koin sovereign dengan perisai pada sisi...

 

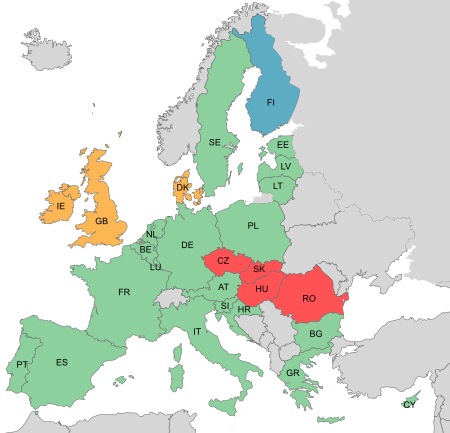
Migration and asylum policy of the European Union

The migration and asylum policy of the European Union is within the area of freedom, security and justice, established to develop and harmonise principles and measures used by member countries of the European Union to regulate migration processes and to manage issues concerning asylum and refugee status in the European Union. History and overview The European Union gained authority to legislate in the area of migration and asylum with the entry into force of the Treaty of Amsterdam on 1 May ...

ピタゴラスの定理

ピタゴラスの定理 種類 定理分野 ユークリッド幾何学命題 2辺 (a, b) 上の2つの正方形の面積の和は、斜辺 (c) 上の正方形の面積に等しくなる。数式 a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} 一般化 余弦定理 空間幾何学 非ユークリッド幾何学 微分幾何学 結果 ピタゴラス数 逆ピタゴラスの定理 複素数 ユークリッド距離 ピタゴラスの三角恒等式 初等幾何学におけるピタゴラ�...

 

Toyota Sprinter

Artikel ini bukan mengenai Mercedes-Benz Sprinter atau Dodge Sprinter. Toyota SprinterInformasiProdusenToyotaJuga disebutChevrolet NovaGeo PrizmToyota Corolla SprinterHolden NovaMasa produksi1968-2001PerakitanToyota City, JepangBodi & rangkaKelasMobil kompakMobil terkaitToyota CorollaToyota TercelToyota Sprinter Trueno Toyota Sprinter Trueno AE86 Toyota Sprinter Carib AE95 Toyota Sprinter adalah mobil kompak berbasis Toyota Corolla yang diproduksi oleh Toyota Motor Corporation di Jep...

 

Batterie au plomb

Pour un article plus général, voir Batterie automobile. Batterie au plomb Batterie d'automobile (12 V, 40 Ah) Caractéristiques Énergie/Poids 20-40 Wh/kg Énergie/Volume 40-100 Wh/ℓ Rendement charge-décharge 50–92[1] % Auto-décharge 3–20 %/mois[2] Durée de vie min. 4 à 5 ans[3] Nombre de cycles de charge 500 à 1 200 Tension nominale par élément 2,1 V modifier  Une batterie au plomb est un accumulateur électrochimique dont les électrodes so...

مقاطعة بابلسر (مازندران)

مقاطعة بابلسر (مازندران) شهرستان بابلسر   Location of Babolsar County in Mazandaran Province تقسيم إداري البلد إيران  [1] العاصمة بابلسر  الدولة  إيران محافظات إيران مازندران خصائص جغرافية إحداثيات 36°40′00″N 52°40′00″E / 36.66667°N 52.66667°E / 36.66667; 52.66667 المساحة 345.70 كيلومتر مربع ...

 

In This Corner (1948 film)

1948 American filmIn This CornerDirected byCharles ReisnerWritten byFred Niblo Jr.Burk SymonProduced byDavid I. StephensonStarringScott BradyAnabel ShawJames MillicanCinematographyGuy RoeEdited byNorman ColbertAlfred DeGaetanoMusic byAlbert GlasserProductioncompanyARC ProductionsDistributed byEagle-Lion FilmsRelease date September 20, 1948 (1948-09-20) Running time59 minutesCountryUnited StatesLanguageEnglish In This Corner is a 1948 American sports drama film directed by Charl...

 

As You Like It

As You Like It adalah sandiwara komedi karya William Shakespeare yang ditulis sekitar tahun 1599-1600. Terjemahan ke dalam bahasa Indonesianya berjudul Manasuka dan dilakukan oleh Trisno Sumardjo.[1] “ Men have died from time to time, and worms have eaten them, but not for love ” Sandiwara ini mengisahkan seorang adipati yang memerintah di Hutan Arden dan saudaranya yang jahat memerintah di kerajaannya. Rosalind dan Celia, dua orang wanita bangsawan, lari ke hutan untuk menghindar...

Espacio euclídeo

Un punto en el espacio euclídeo tridimensional puede ser ubicado por medio de tres coordenadas. El espacio euclídeo (también llamado espacio euclidiano) es un tipo de espacio geométrico donde se satisfacen los axiomas de Euclides de la geometría. La recta real, el plano euclídeo y el espacio tridimensional de la geometría euclidiana son casos especiales de espacios euclidianos de dimensiones 1, 2 y 3 respectivamente. El concepto como conjunto, Rn es la serie de n-adas ordenadas de núm...

 

屋島の戦い

この記事には参考文献や外部リンクの一覧が含まれていますが、脚注による参照が不十分であるため、情報源が依然不明確です。 適切な位置に脚注を追加して、記事の信頼性向上にご協力ください。（2021年3月） 屋島の戦い 屋島の戦い 戦争：治承・寿永の乱 年月日：元暦2年/寿永4年（1185年）2月19日 場所：讃岐国（香川県）屋島（現：高松市） 結果：源氏方の勝利 交...