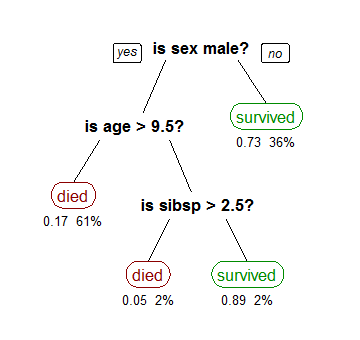Дерево ухвалення рішень
|
Read other articles:

العلاقات السويسرية النيوزيلندية سويسرا نيوزيلندا سويسرا نيوزيلندا تعديل مصدري - تعديل العلاقات السويسرية النيوزيلندية هي العلاقات الثنائية التي تجمع بين سويسرا ونيوزيلندا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدول�...

Об экономическом термине см. Первородный грех (экономика). ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Ран�...

You can help expand this article with text translated from the corresponding article in Russian. (April 2017) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not translate text that appears unreliable or low-...

La Governance della Rai è l'amministrazione della società concessionaria del servizio radiotelevisivo pubblico italiano, la Rai appunto, che include in particolare il Consiglio di amministrazione, che tipicamente nomina i direttori di rete e gli altri direttori editoriali. Tale gestione è stata oggetto di vari interventi legislativi, anche a seguito di numerose pronunce della Corte Costituzionale. La giurisprudenza della Consulta ha infatti riconosciuto che il servizio radiotelevisivo pubb...

The Brief Wondrous Life of Oscar Wao Sampul edisi IndonesiaPengarangJunot DíazPerancang sampulRodrigo CorralNegaraAmerika SerikatBahasaInggris, SpanyolPenerbitRiverheadTanggal terbit6 September, 2007Jenis mediaPrint (hardback and paperback)Halaman352 ppISBNISBN 1-59448-958-0OCLC123539681Desimal Dewey813/.54 22LCCPS3554.I259 B75 2007 The Brief Wondrous Life of Oscar Wao adalah sebuah novel karya Junot Díaz. Meskipun sebuah karya fiksi, novel ini berlatarkan New Jersey di ...

20th-century American journalist Lorena HickokHickok (far right) with Eleanor Roosevelt (2nd from left) in 1933BornLorena Alice Hickok(1893-03-07)March 7, 1893East Troy, Wisconsin, U.S.DiedMay 1, 1968(1968-05-01) (aged 75)Hyde Park, New York, U.S.Resting placeRhinebeck Cemetery (Hyde Park, New York, U.S.)Other namesHickLorena LawrenceOccupation(s)journalist, public relations officialKnown forjournalism, relationship with Eleanor RooseveltParentsAddison HickokAnna Adelsa Wiate H...

豪栄道 豪太郎 場所入りする豪栄道基礎情報四股名 澤井 豪太郎→豪栄道 豪太郎本名 澤井 豪太郎愛称 ゴウタロウ、豪ちゃん、GAD[1][2]生年月日 (1986-04-06) 1986年4月6日(38歳)出身 大阪府寝屋川市身長 183cm体重 160kgBMI 47.26所属部屋 境川部屋得意技 右四つ・出し投げ・切り返し・外掛け・首投げ・右下手投げ成績現在の番付 引退最高位 東大関生涯戦歴 696勝493敗...

Militia maintained by the Slovak People's Party in the period from 1938 to 1945 Not to be confused with Hlinka's Slovak People's Party. Hlinka GuardFlag of the Hlinka GuardEmblem of the Hlinka GuardCommander of Hlinka Guard Interior Minister Alexander Mach and German Interior Minister Wilhelm Frick visit in Nazi GermanyAgency overviewFormed1938Preceding agencyRodobranaDissolved1945TypeParamilitaryJurisdiction Slovak RepublicHeadquartersBratislavaMinisters responsibleJozef Tiso, High Commander...

Hari Santo StefanusNama lainPesta Santo StefanusDirayakan olehUmat KristenJenisKristenTanggal 26 Desember (Barat) 27 Desember (Timur) 9 Januari (Timur) FrekuensiTahunanTerkait denganHari Boxing (bersamaan), Musim Natal, Hari Wren Hari Santo Stefanus atau Pesta Santo Stefanus adalah hari santo Kristen untuk memperingati Santo Stefanus, martir pertama Kristen atau protomartir, dirayakan pada tanggal 26 Desember di Gereja Barat dan 27 Desember di Gereja Timur. Banyak Gereja Ortodoks Timur mengik...

Mountain range along the Pacific coast of Mexico Sierra Madre OccidentalRío Grande de Santiago winding through the Sierra Madre Occidental, forming part of the border between Nayarit and Jalisco.Highest pointPeakCerro MohinoraElevation10,863 ft (3,311 m)Coordinates25°57′22″N 107°2′52″W / 25.95611°N 107.04778°W / 25.95611; -107.04778DimensionsLength932 mi (1,500 km) NW × SEWidth150 mi (240 km) W × EGeography Coun...

Ini adalah nama Maluku, (Ambon) marganya adalah Sahetapy Benjamin Sahetapy Engel Benjamin Sahetapy Engel adalah seorang guru dan politikus Indonesia. Ia lahir di Saparua, Ambon pada tanggal 27 Desember 1916. Ia menimba ilmu di HIK Surakarta pada tahun 1937. Ia adalah anggota partai Fraksi Demokrat. Setelah tamat sekolah, ia bekerja sebagai Guru Christelijke H.I.S. di Banjarmasin, Kupang dan Christelijke H.I.S. Schakelschool Kupang dari 1937 sampai 1942. Pada masa pendudukan Jepang sampai menj...

Icelandic actor (1975–2018) Stefán Karl redirects here. Not to be confused with Steffen Karl. This is an Icelandic name. The last name is patronymic, not a family name; this person is referred to by the given name Stefán Karl. Stefán Karl StefánssonStefán Karl in 2009Born(1975-07-10)10 July 1975Hafnarfjörður, IcelandDied21 August 2018(2018-08-21) (aged 43)Iceland[1]EducationIceland Academy of the ArtsOccupationsActorsingerYears active1994–2018Spouse Steinunn Ólí...

اتحاد كوريا لكرة القدم (بالكورية: 대한축구협회) الاسم المختصر KFA الرياضة كرة القدم كرة القدم الشاطئية كرة قدم الصالات أسس عام 1928 (منذ 96 سنة) الرئيس تشونغ مونغ جون الانتسابات الفيفا : 1948 AFC : 1954 رمز الفيفا KOR الموقع الرسمي www.kfa.or.kr تعديل مصدري - تعديل الشعار السابق ...

Air-filled space near the nasal cavity Ethmoid sinusFrontal view of paranasal sinusesCoronal section of nasal cavities.DetailsNervePosterior ethmoidal nerveIdentifiersLatincellulae ethmoidales, labyrinthi ethmoidalesMeSHD005005TA98A06.1.03.005TA23180FMA84115Anatomical terms of bone[edit on Wikidata] The ethmoid sinuses or ethmoid air cells of the ethmoid bone are one of the four paired paranasal sinuses.[1] Unlike the other three pairs of paranasal sinuses which consist of one or ...

Head of the Catholic Church from 891 to 896 PopeFormosusBishop of RomeChurchCatholic ChurchPapacy began6 October 891Papacy ended4 April 896PredecessorStephen VSuccessorBoniface VIPersonal detailsBornc. 816Rome, Papal StatesDied(896-04-04)4 April 896 (aged c. 80)Rome, Papal States Pope Formosus (c. 816 – 896) was the bishop of Rome and ruler of the Papal States from 6 October 891 until his death on 4 April 896. His reign as pope was troubled, marked by interventions ...

Type of gate in Indonesian architecture A candi bentar marks the entrance into a Balinese temple Pura Lempuyang Luhur, Bali. Candi bentar, or split gateway, is a classical Javanese and Balinese gateway entrance commonly found at the entrance of religious compounds, palaces, or cemeteries in Indonesia.[1] It is a candi-like structure split perfectly in two to create a passage in the center for people to walk through. In contrast to the very ornate shape and decoration of the main faces...

College Board examinations This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: AP Physics – news · newspapers · books · scholar · JSTOR (December 2018) (Learn how and when to remove this message) This article is part of a series onAdvanced Placement Exams • Awards AP Capstone Seminar (AP Capstone Part 1) Research (AP Capstone Par...

Historical form of church membership in American Christianity Half-Way redirects here. For other uses, see Halfway (disambiguation). Part of a series onPuritansThe Puritan, an 1887 statue by Augustus Saint-Gaudens, in Springfield, Massachusetts BackgroundChristianityProtestantismReformationEnglish ReformationCalvinismAnglicanismArminianismArminianism in the Church of EnglandEnglish DissentersIndependentsNonconformismEnglish PresbyterianismEcclesiastical separatism17th-century denominations in...

French journalist, politician, and French Resistance leader Georges MandelGeorges Mandel (5 June 1885 – 7 July 1944) was a French Jewish journalist, and politician. Early life Born Louis George Rothschild in Chatou, Yvelines, he was the son of a tailor and his wife. His family was Jewish, originally from Alsace.[1] They moved into France in 1871 to preserve their French citizenship when Alsace-Lorraine was annexed by the German Empire at the end of the Franco-Prussian War. Early car...

Pour les articles homonymes, voir Heinze (homonymie). Gabriel Heinze Biographie Nom Gabriel Iván Heinze Nationalité Argentin Italien Allemand Nat. sportive Argentin Naissance 19 avril 1978 (46 ans) Crespo (Argentine) Taille 1,77 m (5′ 10″) Période pro. 1996 - 2014 Poste Défenseur centralArrière gauche Pied fort Gauche Parcours senior1 AnnéesClub 0M.0(B.) 1996-1997 Newell's Old Boys 008 0(0) 1997-2001 Real Valladolid 055 0(1) 1998-1999 → Sporting CP 005 0(1) 2001-20...