–ď—Ä–į–ī—Ė—ĒŐĀ–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ (–į–Ĺ–≥–Ľ. gradient descent ) ‚ÄĒ —Ü–Ķ —Ė—ā–Ķ—Ä–į—Ü—Ė–Ļ–Ĺ–ł–Ļ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ –ĺ–Ņ—ā–ł–ľ—Ė–∑–į—Ü—Ė—ó –Ņ–Ķ—Ä—ą–ĺ–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ—É , –≤ —Ź–ļ–ĺ–ľ—É –ī–Ľ—Ź –∑–Ĺ–į—Ö–ĺ–ī–∂–Ķ–Ĺ–Ĺ—Ź –Ľ–ĺ–ļ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ľ—Ė–Ĺ—Ė–ľ—É–ľ—É —Ą—É–Ĺ–ļ—Ü—Ė—ó –∑–ī—Ė–Ļ—Ā–Ĺ—é—é—ā—Ć—Ā—Ź –ļ—Ä–ĺ–ļ–ł, –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü—Ė–Ļ–Ĺ—Ė –Ņ—Ä–ĺ—ā–ł–Ľ–Ķ–∂–Ĺ–ĺ–ľ—É –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—é –≥—Ä–į–ī—Ė—Ē–Ĺ—ā—É (–į–Ī–ĺ –Ĺ–į–Ī–Ľ–ł–∂–Ķ–Ĺ–ĺ–≥–ĺ –≥—Ä–į–ī—Ė—Ē–Ĺ—ā—É) —Ą—É–Ĺ–ļ—Ü—Ė—ó –≤ –Ņ–ĺ—ā–ĺ—á–Ĺ—Ė–Ļ —ā–ĺ—á—Ü—Ė. –Į–ļ—Č–ĺ –Ĺ–į—ā–ĺ–ľ—Ė—Ā—ā—Ć –∑–ī—Ė–Ļ—Ā–Ĺ—é—é—ā—Ć—Ā—Ź –ļ—Ä–ĺ–ļ–ł –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü—Ė–Ļ–Ĺ–ĺ —Ā–į–ľ–ĺ–ľ—É –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—é –≥—Ä–į–ī—Ė—Ē–Ĺ—ā—É, —ā–ĺ –≤—Ė–ī–Ī—É–≤–į—Ē—ā—Ć—Ā—Ź –Ĺ–į–Ī–Ľ–ł–∂–Ķ–Ĺ–Ĺ—Ź –ī–ĺ –Ľ–ĺ–ļ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ľ–į–ļ—Ā–ł–ľ—É–ľ—É —Ü—Ė—Ē—ó —Ą—É–Ĺ–ļ—Ü—Ė—ó; —Ė —Ü—Ź –Ņ—Ä–ĺ—Ü–Ķ–ī—É—Ä–į —ā–ĺ–ī—Ė –≤—Ė–ī–ĺ–ľ–į —Ź–ļ –≥—Ä–į–ī—Ė—ĒŐĀ–Ĺ—ā–Ĺ–ł–Ļ –Ņ—Ė–ī–Ļ–ĺŐĀ–ľ (–į–Ĺ–≥–Ľ. gradient ascent ).
–ď—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ –≤—Ė–ī–ĺ–ľ–ł–Ļ —ā–į–ļ–ĺ–∂ —Ź–ļ –Ĺ–į–Ļ—ą–≤–łŐĀ–ī—ą–ł–Ļ —Ā–Ņ—É—Ā–ļ (–į–Ĺ–≥–Ľ. steepest descent ), –į–Ī–ĺ –ľ–ĶŐĀ—ā–ĺ–ī –Ĺ–į–Ļ—ą–≤–łŐĀ–ī—ą–ĺ–≥–ĺ —Ā–Ņ—ÉŐĀ—Ā–ļ—É (–į–Ĺ–≥–Ľ. method of steepest descent ). –ď—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ –Ĺ–Ķ —Ā–Ľ—Ė–ī –Ņ–Ľ—É—ā–į—ā–ł –∑ –ľ–Ķ—ā–ĺ–ī–ĺ–ľ –Ņ–Ķ—Ä–Ķ–≤–į–Ľ—É [en]
–Ü–Ľ—é—Ā—ā—Ä–į—Ü—Ė—Ź –ľ–Ķ—ā–ĺ–ī—É –Ĺ–į–Ļ—ą–≤–ł–ī—ą–ĺ–≥–ĺ —Ā–Ņ—É—Ā–ļ—É –Ĺ–į —Ä—Ź–ī—Ė –ľ–Ĺ–ĺ–∂–ł–Ĺ —Ä—Ė–≤–Ĺ—Ė–≤ . –ď—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ “Ď—Ä—É–Ĺ—ā—É—Ē—ā—Ć—Ā—Ź –Ĺ–į —ā–ĺ–ľ—É —Ā–Ņ–ĺ—Ā—ā–Ķ—Ä–Ķ–∂–Ķ–Ĺ–Ĺ—Ė, —Č–ĺ —Ź–ļ—Č–ĺ —Ą—É–Ĺ–ļ—Ü—Ė—Ź –ļ—Ė–Ľ—Ć–ļ–ĺ—Ö –∑–ľ—Ė–Ĺ–Ĺ–ł—Ö [en]
F
(
x
)
{\displaystyle F(\mathbf {x} )}
–≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–ĺ—é [en] –ī–ł—Ą–Ķ—Ä–Ķ–Ĺ—Ü—Ė–Ļ–ĺ–≤–Ĺ–ĺ—é –≤ –ĺ–ļ–ĺ–Ľ—Ė —ā–ĺ—á–ļ–ł
a
{\displaystyle \mathbf {a} }
F
(
x
)
{\displaystyle F(\mathbf {x} )}
–Ĺ–į–Ļ—ą–≤–ł–ī—ą–Ķ , —Ź–ļ—Č–ĺ –Ļ—ā–ł –≤—Ė–ī
a
{\displaystyle \mathbf {a} }
F
{\displaystyle F}
a
{\displaystyle \mathbf {a} }
− ‚ąí -->
∇ ‚ąá -->
F
(
a
)
{\displaystyle -\nabla F(\mathbf {a} )}
b
=
a
− ‚ąí -->
γ ő≥ -->
∇ ‚ąá -->
F
(
a
)
{\displaystyle \mathbf {b} =\mathbf {a} -\gamma \nabla F(\mathbf {a} )}
–ī–Ľ—Ź –ī–ĺ—Ā—ā–į—ā–Ĺ—Ć–ĺ –ľ–į–Ľ–ĺ–≥–ĺ
γ ő≥ -->
{\displaystyle \gamma }
F
(
a
)
≥ ‚Č• -->
F
(
b
)
{\displaystyle F(\mathbf {a} )\geq F(\mathbf {b} )}
γ ő≥ -->
∇ ‚ąá -->
F
(
a
)
{\displaystyle \gamma \nabla F(\mathbf {a} )}
a
{\displaystyle \mathbf {a} }
x
0
{\displaystyle \mathbf {x} _{0}}
F
{\displaystyle F}
x
0
,
x
1
,
x
2
,
… ‚Ķ -->
{\displaystyle \mathbf {x} _{0},\mathbf {x} _{1},\mathbf {x} _{2},\dots }
x
n
+
1
=
x
n
− ‚ąí -->
γ ő≥ -->
n
∇ ‚ąá -->
F
(
x
n
)
,
n
≥ ‚Č• -->
0.
{\displaystyle \mathbf {x} _{n+1}=\mathbf {x} _{n}-\gamma _{n}\nabla F(\mathbf {x} _{n}),\ n\geq 0.}
–ú–ł –ľ–į—Ē–ľ–ĺ
F
(
x
0
)
≥ ‚Č• -->
F
(
x
1
)
≥ ‚Č• -->
F
(
x
2
)
≥ ‚Č• -->
⋯ ‚čĮ -->
,
{\displaystyle F(\mathbf {x} _{0})\geq F(\mathbf {x} _{1})\geq F(\mathbf {x} _{2})\geq \cdots ,}
—Ė —ā–ĺ–ľ—É —Ā–Ņ–ĺ–ī—Ė–≤–į—Ē–ľ–ĺ—Ā—Ź, —Č–ĺ –Ņ–ĺ—Ā–Ľ—Ė–ī–ĺ–≤–Ĺ—Ė—Ā—ā—Ć
(
x
n
)
{\displaystyle (\mathbf {x} _{n})}
—Ä–ĺ–∑–ľ—Ė—Ä—É –ļ—Ä–ĺ–ļ—É (–į–Ĺ–≥–Ľ. step size )
γ ő≥ -->
{\displaystyle \gamma }
F
{\displaystyle F}
F
{\displaystyle F}
–ĺ–Ņ—É–ļ–Ľ–ĺ—é , –į
∇ ‚ąá -->
F
{\displaystyle \nabla F}
—É–ľ–ĺ–≤—Ė –õ—Ė–Ņ—ą–ł—Ü—Ź ) —Ė –Ņ–Ķ–≤–Ĺ–ł—Ö –≤–į—Ä—Ė–į–Ĺ—ā–į—Ö –≤–ł–Ī–ĺ—Ä—É
γ ő≥ -->
{\displaystyle \gamma }
–Ľ—Ė–Ĺ—Ė–Ļ–Ĺ–ł–ľ –Ņ–ĺ—ą—É–ļ–ĺ–ľ , —Ź–ļ–ł–Ļ –∑–į–ī–ĺ–≤–ĺ–Ľ—Ć–Ĺ—Ź—Ē —É–ľ–ĺ–≤–ł –í–ĺ–Ľ—Ć—Ą–Ķ ), –∑–Ī—Ė–∂–Ĺ—Ė—Ā—ā—Ć –ī–ĺ –Ľ–ĺ–ļ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ľ—Ė–Ĺ—Ė–ľ—É–ľ—É –ľ–ĺ–∂–Ķ –Ī—É—ā–ł –≥–į—Ä–į–Ĺ—ā–ĺ–≤–į–Ĺ–ĺ. –Į–ļ—Č–ĺ —Ą—É–Ĺ–ļ—Ü—Ė—Ź
F
{\displaystyle F}
–ĺ–Ņ—É–ļ–Ľ–ĺ—é , —ā–ĺ –≤—Ā—Ė –Ľ–ĺ–ļ–į–Ľ—Ć–Ĺ—Ė –ľ—Ė–Ĺ—Ė–ľ—É–ľ–ł —Ē —ā–į–ļ–ĺ–∂ —Ė –≥–Ľ–ĺ–Ī–į–Ľ—Ć–Ĺ–ł–ľ–ł –ľ—Ė–Ĺ—Ė–ľ—É–ľ–į–ľ–ł, —ā–ĺ–ľ—É –≤ —ā–į–ļ–ĺ–ľ—É –≤–ł–Ņ–į–ī–ļ—É –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ –ľ–ĺ–∂–Ķ –∑–Ī—Ė–≥–į—ā–ł—Ā—Ź –ī–ĺ –≥–Ľ–ĺ–Ī–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ä–ĺ–∑–≤'—Ź–∑–ļ—É.
–¶–Ķ–Ļ –Ņ—Ä–ĺ—Ü–Ķ—Ā –Ņ—Ä–ĺ—Ė–Ľ—é—Ā—ā—Ä–ĺ–≤–į–Ĺ–ĺ –Ĺ–į –∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–Ĺ—Ė –Ņ—Ä–į–≤–ĺ—Ä—É—á. –Ę—É—ā –Ņ—Ä–ł–Ņ—É—Ā–ļ–į—Ē—ā—Ć—Ā—Ź, —Č–ĺ
F
{\displaystyle F}
—á–į—ą—Ė . –°–ł–Ĺ—Ė –ļ—Ä–ł–≤—Ė —Ē —Ė–∑–ĺ–Ľ—Ė–Ĺ—Ė—Ź–ľ–ł , —ā–ĺ–Ī—ā–ĺ –ĺ–Ī–Ľ–į—Ā—ā—Ź–ľ–ł, –≤ —Ź–ļ–ł—Ö –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź
F
{\displaystyle F}
–ĺ—Ä—ā–ĺ–≥–ĺ–Ĺ–į–Ľ—Ć–Ĺ–ł–ľ –ī–ĺ —Ė–∑–ĺ–Ľ—Ė–Ĺ—Ė—ó, —Ź–ļ–į –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā—Ć —Ü—Ė—Ē—é —ā–ĺ—á–ļ–ĺ—é. –í–ł–ī–Ĺ–ĺ, —Č–ĺ —Ā–Ņ—É—Ā–ļ –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–ĺ–ľ –≤–Ķ–ī–Ķ –Ĺ–į—Ā –ī–ĺ –ī–Ĺ–į —á–į—ą—Ė, —ā–ĺ–Ī—ā–ĺ –ī–ĺ —ā–ĺ—á–ļ–ł, –≤ —Ź–ļ—Ė–Ļ –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź —Ą—É–Ĺ–ļ—Ü—Ė—ó
F
{\displaystyle F}
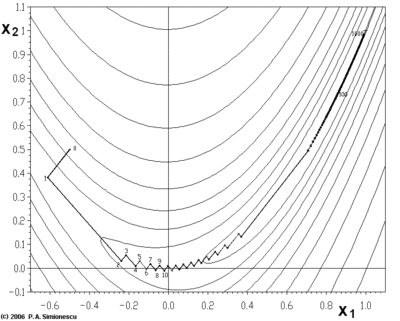
–ď—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ –ľ–į—Ē –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–ł –∑ –Ņ–į—ā–ĺ–Ľ–ĺ–≥—Ė—á–Ĺ–ł–ľ–ł —Ą—É–Ĺ–ļ—Ü—Ė—Ź–ľ–ł, —ā–į–ļ–ł–ľ–ł —Ź–ļ –Ņ–ĺ–ļ–į–∑–į–Ĺ–į —ā—É—ā —Ą—É–Ĺ–ļ—Ü—Ė—Ź –†–ĺ–∑–Ķ–Ĺ–Ī—Ä–ĺ–ļ–į .
f
(
x
1
,
x
2
)
=
(
1
− ‚ąí -->
x
1
)
2
+
100
(
x
2
− ‚ąí -->
x
1
2
)
2
.
{\displaystyle f(x_{1},x_{2})=(1-x_{1})^{2}+100(x_{2}-x_{1}^{2})^{2}.\quad }
–§—É–Ĺ–ļ—Ü—Ė—Ź –†–ĺ–∑–Ķ–Ĺ–Ī—Ä–ĺ–ļ–į –ľ–į—Ē –≤—É–∑—Ć–ļ—É –≤–ł–≥–Ĺ—É—ā—É –ī–ĺ–Ľ–ł–Ĺ—É, —Ź–ļ–į –ľ—Ė—Ā—ā–ł—ā—Ć –ľ—Ė–Ĺ—Ė–ľ—É–ľ. –Ē–Ĺ–ĺ —Ü—Ė—Ē—ó –ī–ĺ–Ľ–ł–Ĺ–ł —Ē –ī—É–∂–Ķ –Ņ–ĺ–Ľ–ĺ–≥–ł–ľ. –ß–Ķ—Ä–Ķ–∑ –≤–ł–≥–Ĺ—É—ā—Ė—Ā—ā—Ć –Ņ–ĺ–Ľ–ĺ–≥–ĺ—ó –ī–ĺ–Ľ–ł–Ĺ–ł –ĺ–Ņ—ā–ł–ľ—Ė–∑–į—Ü—Ė—Ź –Ņ–ĺ–≤—Ė–Ľ—Ć–Ĺ–ĺ —Ä—É—Ö–į—Ē—ā—Ć—Ā—Ź –≤ –Ĺ–į–Ņ—Ä—Ź–ľ–ļ—É –ľ—Ė–Ĺ—Ė–ľ—É–ľ—É –∑–ł“Ď–∑–į“Ď–ĺ–ľ –ļ—Ä–ĺ–ļ–į–ľ–ł –ľ–į–Ľ–ĺ–≥–ĺ —Ä–ĺ–∑–ľ—Ė—Ä—É.
¬ę–ó–ł“Ď–∑–į“Ď–ĺ–Ņ–ĺ–ī—Ė–Ī–Ĺ–į¬Ľ –Ņ—Ä–ł—Ä–ĺ–ī–į —Ü—Ć–ĺ–≥–ĺ –ľ–Ķ—ā–ĺ–ī—É —ā–į–ļ–ĺ–∂ —Ē –ĺ—á–Ķ–≤–ł–ī–Ĺ–ĺ—é –Ĺ–ł–∂—á–Ķ, –ī–Ķ –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ –∑–į—Ā—ā–ĺ—Ā–ĺ–≤–į–Ĺ–ĺ –ī–ĺ
F
(
x
,
y
)
=
sin
‚Ā° -->
(
1
2
x
2
− ‚ąí -->
1
4
y
2
+
3
)
cos
‚Ā° -->
(
2
x
+
1
− ‚ąí -->
e
y
)
{\displaystyle F(x,y)=\sin \left({\frac {1}{2}}x^{2}-{\frac {1}{4}}y^{2}+3\right)\cos(2x+1-e^{y})}
–Ē–Ľ—Ź –ī–Ķ—Ź–ļ–ł—Ö —Ė–∑ –Ĺ–į–≤–Ķ–ī–Ķ–Ĺ–ł—Ö –≤–ł—Č–Ķ –Ņ—Ä–ł–ļ–Ľ–į–ī—Ė–≤ –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ —Ē –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ –Ņ–ĺ–≤—Ė–Ľ—Ć–Ĺ–ł–ľ –Ņ–ĺ–Ī–Ľ–ł–∑—É –ľ—Ė–Ĺ—Ė–ľ—É–ľ—É: –∑ —ā–Ķ—Ö–Ĺ—Ė—á–Ĺ–ĺ—ó —ā–ĺ—á–ļ–ł –∑–ĺ—Ä—É, –Ļ–ĺ–≥–ĺ –į—Ā–ł–ľ–Ņ—ā–ĺ—ā–ł—á–Ĺ–ł–Ļ —ā–Ķ–ľ–Ņ –∑–Ī—Ė–≥–į–Ĺ–Ĺ—Ź –Ņ–ĺ—Ā—ā—É–Ņ–į—Ē—ā—Ć—Ā—Ź –Ī–į–≥–į—ā—Ć–ĺ–ľ —Ė–Ĺ—ą–ł–ľ –ľ–Ķ—ā–ĺ–ī–į–ľ. –Ē–Ľ—Ź –Ĺ–Ķ–≤–ī–į–Ľ–ĺ –ĺ–Ī—É–ľ–ĺ–≤–Ľ–Ķ–Ĺ–ł—Ö –ĺ–Ņ—É–ļ–Ľ–ł—Ö –∑–į–ī–į—á –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ ¬ę–∑–ł“Ď–∑–į“Ď—É—Ē¬Ľ –≤—Ā–Ķ –Ī—Ė–Ľ—Ć—ą–Ķ, –ļ–ĺ–Ľ–ł –≥—Ä–į–ī—Ė—Ē–Ĺ—ā –≤–ļ–į–∑—É—Ē –ľ–į–Ļ–∂–Ķ –ĺ—Ä—ā–ĺ–≥–ĺ–Ĺ–į–Ľ—Ć–Ĺ–ĺ –ī–ĺ –Ĺ–į–Ļ–ļ–ĺ—Ä–ĺ—ā—ą–ĺ–≥–ĺ –Ĺ–į–Ņ—Ä—Ź–ľ—É –ī–ĺ —ā–ĺ—á–ļ–ł –ľ—Ė–Ĺ—Ė–ľ—É–ľ—É. –Ē–ĺ–ļ–Ľ–į–ī–Ĺ—Ė—ą–Ķ –ī–ł–≤. –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä—Ė –Ĺ–ł–∂—á–Ķ.
–Ē–Ľ—Ź –Ĺ–Ķ–ī–ł—Ą–Ķ—Ä–Ķ–Ĺ—Ü—Ė–Ļ–ĺ–≤–Ĺ–ł—Ö —Ą—É–Ĺ–ļ—Ü—Ė–Ļ –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ—Ė –ľ–Ķ—ā–ĺ–ī–ł —Ē –Ĺ–Ķ–ī–ĺ—Ā—ā–į—ā–Ĺ—Ć–ĺ –≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–ł–ľ–ł. –Ē–Ľ—Ź –Ľ–ĺ–ļ–į–Ľ—Ć–Ĺ–ĺ –Ľ—Ė–Ņ—ą–ł—Ü–Ķ–≤–ł—Ö –∑–į–ī–į—á, —ā–į –ĺ—Ā–ĺ–Ī–Ľ–ł–≤–ĺ –ī–Ľ—Ź –∑–į–ī–į—á –ĺ–Ņ—É–ļ–Ľ–ĺ—ó –ĺ–Ņ—ā–ł–ľ—Ė–∑–į—Ü—Ė—ó , —Ü—Ė–Ľ–ļ–ĺ–ľ –≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–ł–ľ–ł —Ē –≤'—Ź–∑–ļ–ĺ–≤—Ė –ľ–Ķ—ā–ĺ–ī–ł —Ā–Ņ—É—Ā–ļ—É . –Ę–į–ļ–ĺ–∂ –ľ–ĺ–∂—É—ā—Ć –∑–į—Ā—ā–ĺ—Ā–ĺ–≤—É–≤–į—ā–ł—Ā—Ź –Ĺ–Ķ-—Ā–Ņ—É—Ā–ļ–ĺ–≤—Ė –ľ–Ķ—ā–ĺ–ī–ł, —ā–į–ļ—Ė —Ź–ļ –ľ–Ķ—ā–ĺ–ī–ł —Ā—É–Ī–≥—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ĺ—ó –Ņ—Ä–ĺ—Ē–ļ—Ü—Ė—ó.[ 1]
–ď—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ –ľ–ĺ–∂–Ķ –∑–į—Ā—ā–ĺ—Ā–ĺ–≤—É–≤–į—ā–ł—Ā—Ź –ī–Ľ—Ź —Ä–ĺ–∑–≤'—Ź–∑–į–Ĺ–Ĺ—Ź —Ā–ł—Ā—ā–Ķ–ľ–ł –Ľ—Ė–Ĺ—Ė–Ļ–Ĺ–ł—Ö —Ä—Ė–≤–Ĺ—Ź–Ĺ—Ć , –Ņ–Ķ—Ä–Ķ—Ą–ĺ—Ä–ľ—É–Ľ—Ć–ĺ–≤–į–Ĺ–ĺ–≥–ĺ —Ź–ļ –∑–į–ī–į—á–į –ļ–≤–į–ī—Ä–į—ā–ł—á–Ĺ–ĺ—ó –ľ—Ė–Ĺ—Ė–ľ—Ė–∑–į—Ü—Ė—ó, –Ĺ–į–Ņ—Ä–ł–ļ–Ľ–į–ī, —Ė–∑ –∑–į—Ā—ā–ĺ—Ā—É–≤–į–Ĺ–Ĺ—Ź–ľ –ľ–Ķ—ā–ĺ–ī—É –Ĺ–į–Ļ–ľ–Ķ–Ĺ—ą–ł—Ö –ļ–≤–į–ī—Ä–į—ā—Ė–≤ . –†–ĺ–∑–≤'—Ź–∑–ĺ–ļ
A
x
− ‚ąí -->
b
=
0
{\displaystyle A\mathbf {x} -\mathbf {b} =0}
—É —Ā–Ķ–Ĺ—Ā—Ė –ľ–Ķ—ā–ĺ–ī—É –Ĺ–į–Ļ–ľ–Ķ–Ĺ—ą–ł—Ö –ļ–≤–į–ī—Ä–į—ā—Ė–≤ –≤–ł–∑–Ĺ–į—á–į—Ē—ā—Ć—Ā—Ź —Ź–ļ –ľ—Ė–Ĺ—Ė–ľ—Ė–∑–į—Ü—Ė—Ź —Ą—É–Ĺ–ļ—Ü—Ė—ó
F
(
x
)
=
‖ ‚ÄĖ -->
A
x
− ‚ąí -->
b
‖ ‚ÄĖ -->
2
.
{\displaystyle F(\mathbf {x} )=\|A\mathbf {x} -\mathbf {b} \|^{2}.}
–í —ā—Ä–į–ī–ł—Ü—Ė–Ļ–Ĺ–ĺ–ľ—É –ľ–Ķ—ā–ĺ–ī—Ė –Ĺ–į–Ļ–ľ–Ķ–Ĺ—ą–ł—Ö –ļ–≤–į–ī—Ä–į—ā—Ė–≤ –ī–Ľ—Ź –ī—Ė–Ļ—Ā–Ĺ–ł—Ö
A
{\displaystyle A}
b
{\displaystyle \mathbf {b} }
–Ķ–≤–ļ–Ľ—Ė–ī–ĺ–≤–į –Ĺ–ĺ—Ä–ľ–į , —Ė –≤ —Ü—Ć–ĺ–ľ—É –≤–ł–Ņ–į–ī–ļ—É
∇ ‚ąá -->
F
(
x
)
=
2
A
T
(
A
x
− ‚ąí -->
b
)
.
{\displaystyle \nabla F(\mathbf {x} )=2A^{T}(A\mathbf {x} -\mathbf {b} ).}
–í —ā–į–ļ–ĺ–ľ—É –≤–ł–Ņ–į–ī–ļ—É –ľ—Ė–Ĺ—Ė–ľ—Ė–∑–į—Ü—Ė—Ź –Ľ—Ė–Ĺ—Ė–Ļ–Ĺ–ł–ľ –Ņ–ĺ—ą—É–ļ–ĺ–ľ , —Ź–ļ–į –∑–Ĺ–į—Ö–ĺ–ī–ł—ā—Ć –Ĺ–į –ļ–ĺ–∂–Ĺ—Ė–Ļ —Ė—ā–Ķ—Ä–į—Ü—Ė—ó –Ľ–ĺ–ļ–į–Ľ—Ć–Ĺ–ĺ –ĺ–Ņ—ā–ł–ľ–į–Ľ—Ć–Ĺ–ł–Ļ —Ä–ĺ–∑–ľ—Ė—Ä –ļ—Ä–ĺ–ļ—É
γ ő≥ -->
{\displaystyle \gamma }
γ ő≥ -->
{\displaystyle \gamma }
[ 2]
–Ē–Ľ—Ź —Ä–ĺ–∑–≤'—Ź–∑–į–Ĺ–Ĺ—Ź –Ľ—Ė–Ĺ—Ė–Ļ–Ĺ–ł—Ö —Ä—Ė–≤–Ĺ—Ź–Ĺ—Ć –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ –∑–į—Ā—ā–ĺ—Ā–ĺ–≤—É—Ē—ā—Ć—Ā—Ź —Ä—Ė–ī–ļ–ĺ, –į –ĺ–ī–Ĺ—Ė—Ē—é –∑ –Ĺ–į–Ļ–Ņ–ĺ–Ņ—É–Ľ—Ź—Ä–Ĺ—Ė—ą–ł—Ö –į–Ľ—Ć—ā–Ķ—Ä–Ĺ–į—ā–ł–≤ —Ē –ľ–Ķ—ā–ĺ–ī —Ā–Ņ—Ä—Ź–∂–Ķ–Ĺ–ł—Ö –≥—Ä–į–ī—Ė—Ē–Ĺ—ā—Ė–≤ . –®–≤–ł–ī–ļ—Ė—Ā—ā—Ć –∑–Ī—Ė–≥–į–Ĺ–Ĺ—Ź –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ĺ–≥–ĺ —Ā–Ņ—É—Ā–ļ—É –∑–į–Ľ–Ķ–∂–ł—ā—Ć –≤—Ė–ī –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā–į –ľ—Ė–Ĺ—Ė–ľ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –≤–Ľ–į—Ā–Ĺ–ł—Ö –∑–Ĺ–į—á–Ķ–Ĺ—Ć
A
{\displaystyle A}
—Ā–Ņ—Ä—Ź–∂–Ķ–Ĺ–ł—Ö –≥—Ä–į–ī—Ė—Ē–Ĺ—ā—Ė–≤ –ľ–į—Ē —Ā–ļ–Ľ–į–ī–Ĺ—Ė—ą—É –∑–į–Ľ–Ķ–∂–Ĺ—Ė—Ā—ā—Ć –≤—Ė–ī —Ü–ł—Ö –≤–Ľ–į—Ā–Ĺ–ł—Ö –∑–Ĺ–į—á–Ķ–Ĺ—Ć, —Ė –ľ–ĺ–∂–Ķ –ĺ—ā—Ä–ł–ľ—É–≤–į—ā–ł –ļ–ĺ—Ä–ł—Ā—ā—Ć –≤—Ė–ī –Ņ–Ķ—Ä–Ķ–ī–ĺ–Ī—É–ľ–ĺ–≤–Ľ—é–≤–į–Ĺ–Ĺ—Ź [en]
–ď—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ –ľ–ĺ–∂–Ķ —ā–į–ļ–ĺ–∂ –∑–į—Ā—ā–ĺ—Ā–ĺ–≤—É–≤–į—ā–ł—Ā—Ź —Ė –ī–ĺ —Ä–ĺ–∑–≤'—Ź–∑–į–Ĺ–Ĺ—Ź —Ā–ł—Ā—ā–Ķ–ľ –Ĺ–Ķ–Ľ—Ė–Ĺ—Ė–Ļ–Ĺ–ł—Ö —Ä—Ė–≤–Ĺ—Ź–Ĺ—Ć. –Ě–ł–∂—á–Ķ –Ĺ–į–≤–Ķ–ī–Ķ–Ĺ–ĺ –Ņ—Ä–ł–ļ–Ľ–į–ī, —Ź–ļ –∑–į—Ā—ā–ĺ—Ā–ĺ–≤—É–≤–į—ā–ł –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ –ī–Ľ—Ź —Ä–ĺ–∑–≤'—Ź–∑–į–Ĺ–Ĺ—Ź –ī–Ľ—Ź —ā—Ä—Ć–ĺ—Ö –Ĺ–Ķ–≤—Ė–ī–ĺ–ľ–ł—Ö –∑–ľ—Ė–Ĺ–Ĺ–ł—Ö, x 1 , x 2 —ā–į x 3 . –¶–Ķ–Ļ –Ņ—Ä–ł–ļ–Ľ–į–ī –Ņ–ĺ–ļ–į–∑—É—Ē –ĺ–ī–Ĺ—É —Ė—ā–Ķ—Ä–į—Ü—Ė—é –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ĺ–≥–ĺ —Ā–Ņ—É—Ā–ļ—É.
–†–ĺ–∑–≥–Ľ—Ź–Ĺ—Ć–ľ–ĺ —Ā–ł—Ā—ā–Ķ–ľ—É –Ĺ–Ķ–Ľ—Ė–Ĺ—Ė–Ļ–Ĺ–ł—Ö —Ä—Ė–≤–Ĺ—Ź–Ĺ—Ć
{
3
x
1
− ‚ąí -->
cos
‚Ā° -->
(
x
2
x
3
)
− ‚ąí -->
3
2
=
0
4
x
1
2
− ‚ąí -->
625
x
2
2
+
2
x
2
− ‚ąí -->
1
=
0
exp
‚Ā° -->
(
− ‚ąí -->
x
1
x
2
)
+
20
x
3
+
10
π ŌÄ -->
− ‚ąí -->
3
3
=
0
{\displaystyle {\begin{cases}3x_{1}-\cos(x_{2}x_{3})-{\tfrac {3}{2}}=0\\4x_{1}^{2}-625x_{2}^{2}+2x_{2}-1=0\\\exp(-x_{1}x_{2})+20x_{3}+{\tfrac {10\pi -3}{3}}=0\end{cases}}}
–Ņ—Ä–ł–Ņ—É—Ā—ā—Ė–ľ–ĺ, —Č–ĺ –ľ–ł –ľ–į—Ē–ľ–ĺ —Ą—É–Ĺ–ļ—Ü—Ė—é
G
(
x
)
=
[
3
x
1
− ‚ąí -->
cos
‚Ā° -->
(
x
2
x
3
)
− ‚ąí -->
3
2
4
x
1
2
− ‚ąí -->
625
x
2
2
+
2
x
2
− ‚ąí -->
1
exp
‚Ā° -->
(
− ‚ąí -->
x
1
x
2
)
+
20
x
3
+
10
π ŌÄ -->
− ‚ąí -->
3
3
]
{\displaystyle G(\mathbf {x} )={\begin{bmatrix}3x_{1}-\cos(x_{2}x_{3})-{\tfrac {3}{2}}\\4x_{1}^{2}-625x_{2}^{2}+2x_{2}-1\\\exp(-x_{1}x_{2})+20x_{3}+{\tfrac {10\pi -3}{3}}\\\end{bmatrix}}}
–ī–Ķ
x
=
[
x
1
x
2
x
3
]
{\displaystyle \mathbf {x} ={\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\\\end{bmatrix}}}
—ā–į —Ü—Ė–Ľ—Ć–ĺ–≤—É —Ą—É–Ĺ–ļ—Ü—Ė—é
F
(
x
)
=
1
2
G
T
(
x
)
G
(
x
)
=
1
2
(
(
3
x
1
− ‚ąí -->
cos
‚Ā° -->
(
x
2
x
3
)
− ‚ąí -->
3
2
)
2
+
(
4
x
1
2
− ‚ąí -->
625
x
2
2
+
2
x
2
− ‚ąí -->
1
)
2
+
(
exp
‚Ā° -->
(
− ‚ąí -->
x
1
x
2
)
+
20
x
3
+
1
3
(
10
π ŌÄ -->
− ‚ąí -->
3
)
)
2
)
{\displaystyle F(\mathbf {x} )={\tfrac {1}{2}}G^{\mathrm {T} }(\mathbf {x} )G(\mathbf {x} )={\tfrac {1}{2}}\left(\left(3x_{1}-\cos(x_{2}x_{3})-{\tfrac {3}{2}}\right)^{2}+\left(4x_{1}^{2}-625x_{2}^{2}+2x_{2}-1\right)^{2}+\left(\exp(-x_{1}x_{2})+20x_{3}+{\tfrac {1}{3}}(10\pi -3)\right)^{2}\right)}
–∑ –Ņ–ĺ—á–į—ā–ļ–ĺ–≤–ł–ľ –Ņ—Ä–ł–Ņ—É—Č–Ķ–Ĺ–Ĺ—Ź–ľ
x
(
0
)
=
[
x
1
x
2
x
3
]
=
[
0
0
0
]
{\displaystyle \mathbf {x} ^{(0)}={\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\\\end{bmatrix}}={\begin{bmatrix}0\\0\\0\\\end{bmatrix}}}
–ú–ł –∑–Ĺ–į—Ē–ľ–ĺ, —Č–ĺ
x
(
1
)
=
x
(
0
)
− ‚ąí -->
γ ő≥ -->
0
∇ ‚ąá -->
F
(
x
(
0
)
)
{\displaystyle \mathbf {x} ^{(1)}=\mathbf {x} ^{(0)}-\gamma _{0}\nabla F(\mathbf {x} ^{(0)})}
–ī–Ķ
∇ ‚ąá -->
F
(
x
(
0
)
)
=
J
G
(
x
(
0
)
)
T
G
(
x
(
0
)
)
{\displaystyle \nabla F(\mathbf {x} ^{(0)})=J_{G}(\mathbf {x} ^{(0)})^{\mathrm {T} }G(\mathbf {x} ^{(0)})}
–ú–į—ā—Ä–ł—Ü—Ź –Į–ļ–ĺ–Ī—Ė
J
G
(
x
(
0
)
)
{\displaystyle J_{G}(\mathbf {x} ^{(0)})}
J
G
=
[
3
sin
‚Ā° -->
(
x
2
x
3
)
x
3
sin
‚Ā° -->
(
x
2
x
3
)
x
2
8
x
1
− ‚ąí -->
1250
x
2
+
2
0
− ‚ąí -->
x
2
exp
‚Ā° -->
(
− ‚ąí -->
x
1
x
2
)
− ‚ąí -->
x
1
exp
‚Ā° -->
(
− ‚ąí -->
x
1
x
2
)
20
]
{\displaystyle J_{G}={\begin{bmatrix}3&\sin(x_{2}x_{3})x_{3}&\sin(x_{2}x_{3})x_{2}\\8x_{1}&-1250x_{2}+2&0\\-x_{2}\exp {(-x_{1}x_{2})}&-x_{1}\exp(-x_{1}x_{2})&20\\\end{bmatrix}}}
–ü–ĺ—ā—Ė–ľ –ĺ–Ī—á–ł—Ā–Ľ—Ė–ľ–ĺ —Ü—Ė —á–Ľ–Ķ–Ĺ–ł –≤
x
(
0
)
{\displaystyle \mathbf {x} ^{(0)}}
J
G
(
x
(
0
)
)
=
[
3
0
0
0
2
0
0
0
20
]
,
G
(
x
(
0
)
)
=
[
− ‚ąí -->
2.5
− ‚ąí -->
1
10.472
]
{\displaystyle J_{G}\left(\mathbf {x} ^{(0)}\right)={\begin{bmatrix}3&0&0\\0&2&0\\0&0&20\end{bmatrix}},\qquad G(\mathbf {x} ^{(0)})={\begin{bmatrix}-2.5\\-1\\10.472\end{bmatrix}}}
–ě—ā–∂–Ķ,
x
(
1
)
=
0
− ‚ąí -->
γ ő≥ -->
0
[
− ‚ąí -->
7.5
− ‚ąí -->
2
209.44
]
{\displaystyle \mathbf {x} ^{(1)}=0-\gamma _{0}{\begin{bmatrix}-7.5\\-2\\209.44\end{bmatrix}}}
—ā–į
F
(
x
(
0
)
)
=
0.5
(
(
− ‚ąí -->
2.5
)
2
+
(
− ‚ąí -->
1
)
2
+
(
10.472
)
2
)
=
58.456
{\displaystyle F\left(\mathbf {x} ^{(0)}\right)=0.5\left((-2.5)^{2}+(-1)^{2}+(10.472)^{2}\right)=58.456}
–ź–Ĺ—Ė–ľ–į—Ü—Ė—Ź, —Ź–ļ–į –Ņ–ĺ–ļ–į–∑—É—Ē –Ņ–Ķ—Ä—ą—Ė 83 —Ė—ā–Ķ—Ä–į—Ü—Ė—ó –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ĺ–≥–ĺ —Ā–Ņ—É—Ā–ļ—É, —Č–ĺ –∑–į—Ā—ā–ĺ—Ā–ĺ–≤—É—Ē—ā—Ć—Ā—Ź –ī–ĺ —Ü—Ć–ĺ–≥–ĺ –Ņ—Ä–ł–ļ–Ľ–į–ī—É. –ü–ĺ–≤–Ķ—Ä—Ö–Ĺ—Ė —Ē —Ė–∑–ĺ–Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ—Ź–ľ–ł
F
(
x
(
n
)
)
{\displaystyle F(\mathbf {x} ^{(n)})}
x
(
n
)
{\displaystyle \mathbf {x} ^{(n)}}
–Ę–Ķ–Ņ–Ķ—Ä –ľ—É—Ā–ł—ā—Ć –Ī—É—ā–ł –∑–Ĺ–į–Ļ–ī–Ķ–Ĺ–ĺ –Ņ—Ä–ł–ī–į—ā–Ĺ–ł–Ļ
γ ő≥ -->
0
{\displaystyle \gamma _{0}}
F
(
x
(
1
)
)
≤ ‚ȧ -->
F
(
x
(
0
)
)
{\displaystyle F(\mathbf {x} ^{(1)})\leq F(\mathbf {x} ^{(0)})}
–Ľ—Ė–Ĺ—Ė–Ļ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ—ą—É–ļ—É . –ú–ĺ–∂–Ĺ–į —ā–į–ļ–ĺ–∂ –Ņ—Ä–ĺ—Ā—ā–ĺ –Ņ—Ä–ł–Ņ—É—Ā—ā–ł—ā–ł
γ ő≥ -->
0
=
0.001
{\displaystyle \gamma _{0}=0.001}
x
(
1
)
=
[
0.0075
0.002
− ‚ąí -->
0.20944
]
{\displaystyle \mathbf {x} ^{(1)}={\begin{bmatrix}0.0075\\0.002\\-0.20944\\\end{bmatrix}}}
–ü—Ä–ł –ĺ–Ī—á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ—Ė –Ĺ–į —Ü—Ć–ĺ–ľ—É –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ė
F
(
x
(
1
)
)
=
0.5
(
(
− ‚ąí -->
2.48
)
2
+
(
− ‚ąí -->
1.00
)
2
+
(
6.28
)
2
)
=
23.306
{\displaystyle F\left(\mathbf {x} ^{(1)}\right)=0.5\left((-2.48)^{2}+(-1.00)^{2}+(6.28)^{2}\right)=23.306}
–ó–ľ–Ķ–Ĺ—ą–Ķ–Ĺ–Ĺ—Ź –∑
F
(
x
(
0
)
)
=
58.456
{\displaystyle F(\mathbf {x} ^{(0)})=58.456}
F
(
x
(
1
)
)
=
23.306
{\displaystyle F(\mathbf {x} ^{(1)})=23.306}
–ď—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ –Ņ—Ä–į—Ü—é—Ē –≤ –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä–į—Ö –∑ –Ī—É–ī—Ć-—Ź–ļ–ł–ľ —á–ł—Ā–Ľ–ĺ–ľ –≤–ł–ľ—Ė—Ä—Ė–≤, –Ĺ–į–≤—Ė—ā—Ć —É –Ĺ–Ķ—Ā–ļ—Ė–Ĺ—á–Ķ–Ĺ–Ĺ–ĺ–≤–ł–ľ—Ė—Ä–Ĺ–ł—Ö . –í –ĺ—Ā—ā–į–Ĺ–Ĺ—Ć–ĺ–ľ—É –≤–ł–Ņ–į–ī–ļ—É –Ņ—Ä–ĺ—Ā—ā—Ė—Ä –Ņ–ĺ—ą—É–ļ—É –∑–į–∑–≤–ł—á–į–Ļ —Ē –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä–ĺ–ľ —Ą—É–Ĺ–ļ—Ü—Ė–Ļ , —Ė –ī–Ľ—Ź –≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź –Ĺ–į–Ņ—Ä—Ź–ľ–ļ—É —Ā–Ņ—É—Ā–ļ—É –∑–ī—Ė–Ļ—Ā–Ĺ—é—Ē—ā—Ć—Ā—Ź –ĺ–Ī—á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ—Ź –Ņ–ĺ—Ö—Ė–ī–Ĺ–ĺ—ó –ď–į—ā–ĺ —Ą—É–Ĺ–ļ—Ü—Ė–ĺ–Ĺ–į–Ľ—É, —Ź–ļ–ł–Ļ –ľ—Ė–Ĺ—Ė–ľ—Ė–∑—É—é—ā—Ć.[ 3]
–Į–ļ—Č–ĺ –ļ—Ä–ł–≤–ł–Ĺ–į –∑–į–ī–į–Ĺ–ĺ—ó —Ą—É–Ĺ–ļ—Ü—Ė—ó –ī—É–∂–Ķ —Ä—Ė–∑–Ĺ–ł—ā—Ć—Ā—Ź –≤ —Ä—Ė–∑–Ĺ–ł—Ö –Ĺ–į–Ņ—Ä—Ź–ľ–ļ–į—Ö, —ā–ĺ –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ĺ–ľ—É —Ā–Ņ—É—Ā–ļ–ĺ–≤—Ė –ľ–ĺ–∂–Ķ –∑–Ĺ–į–ī–ĺ–Ī–ł—ā–ł—Ā—Ź –Ī–į–≥–į—ā–ĺ —Ė—ā–Ķ—Ä–į—Ü—Ė–Ļ –ī–Ľ—Ź –ĺ–Ī—á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ—Ź –Ľ–ĺ–ļ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ľ—Ė–Ĺ—Ė–ľ—É–ľ—É –∑ –Ņ–ĺ—ā—Ä—Ė–Ī–Ĺ–ĺ—é —ā–ĺ—á–Ĺ—Ė—Ā—ā—é . –Ē–Ľ—Ź —ā–į–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü—Ė–Ļ –Ņ–ĺ–≤—Ė–Ľ—Ć–Ĺ–Ķ –∑–Ī—Ė–≥–į–Ĺ–Ĺ—Ź –Ľ—Ė–ļ—É—Ē—ā—Ć—Ā—Ź –Ņ–Ķ—Ä–Ķ–ī–ĺ–Ī—É–ľ–ĺ–≤–Ľ—é–≤–į–Ĺ–Ĺ—Ź–ľ [en] –ļ–ĺ–Ĺ—Ü–Ķ–Ĺ—ā—Ä–ł—á–Ĺ–ł—Ö –ļ—Ė–Ľ . –ü—Ä–ĺ—ā–Ķ –Ņ–ĺ–Ī—É–ī–ĺ–≤–į —ā–į –∑–į—Ā—ā–ĺ—Ā—É–≤–į–Ĺ–Ĺ—Ź –Ņ–Ķ—Ä–Ķ–ī–ĺ–Ī—É–ľ–ĺ–≤–Ľ—é–≤–į–Ĺ–Ĺ—Ź –ľ–ĺ–∂—É—ā—Ć –Ī—É—ā–ł –ĺ–Ī—á–ł—Ā–Ľ—é–≤–į–Ľ—Ć–Ĺ–ĺ –≤–ł—ā—Ä–į—ā–Ĺ–ł–ľ–ł.
–ď—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ –ľ–ĺ–∂–Ĺ–į –Ņ–ĺ—Ē–ī–Ĺ—É–≤–į—ā–ł –∑ –Ľ—Ė–Ĺ—Ė–Ļ–Ĺ–ł–ľ –Ņ–ĺ—ą—É–ļ–ĺ–ľ , —Ź–ļ–ł–Ļ –Ĺ–į –ļ–ĺ–∂–Ĺ—Ė–Ļ —Ė—ā–Ķ—Ä–į—Ü—Ė—ó —ą—É–ļ–į—Ē –Ľ–ĺ–ļ–į–Ľ—Ć–Ĺ–ĺ –ĺ–Ņ—ā–ł–ľ–į–Ľ—Ć–Ĺ–ł–Ļ —Ä–ĺ–∑–ľ—Ė—Ä –ļ—Ä–ĺ–ļ—É
γ ő≥ -->
{\displaystyle \gamma }
γ ő≥ -->
{\displaystyle \gamma }
–ö—Ä–į—Č–ł–ľ–ł –į–Ľ—Ć—ā–Ķ—Ä–Ĺ–į—ā–ł–≤–į–ľ–ł –ľ–ĺ–∂—É—ā—Ć –Ī—É—ā–ł –ľ–Ķ—ā–ĺ–ī–ł –Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤—Ė –ľ–Ķ—ā–ĺ–ī—É –Ě—Ć—é—ā–ĺ–Ĺ–į —ā–į –ĺ–Ī–Ķ—Ä–Ĺ–Ķ–Ĺ–Ĺ—Ź –≥–Ķ—Ā—Ā—Ė–į–Ĺ—É —Ė–∑ –∑–į—Ā—ā–ĺ—Ā—É–≤–į–Ĺ–Ĺ—Ź–ľ –ľ–Ķ—ā–ĺ–ī–ł–ļ —Ā–Ņ—Ä—Ź–∂–Ķ–Ĺ–ł—Ö –≥—Ä–į–ī—Ė—Ē–Ĺ—ā—Ė–≤ .[ 4] [ 5] –ú–Ķ—ā–ĺ–ī –Ď–§–ď–® , —Ź–ļ–ł–Ļ —Ā–ļ–Ľ–į–ī–į—Ē—ā—Ć—Ā—Ź –∑ –ĺ–Ī—á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ—Ź –Ĺ–į –ļ–ĺ–∂–Ĺ–ĺ–ľ—É –ļ—Ä–ĺ—Ü—Ė –ľ–į—ā—Ä–ł—Ü—Ė, –Ĺ–į —Ź–ļ—É –ľ–Ĺ–ĺ–∂–ł—ā—Ć—Ā—Ź –≤–Ķ–ļ—ā–ĺ—Ä –≥—Ä–į–ī—Ė—Ē–Ĺ—ā—É, —Č–ĺ–Ī–ł –Ļ—ā–ł –≤ ¬ę–Ĺ–į–Ļ–ļ—Ä–į—Č–ĺ–ľ—ɬĽ –Ĺ–į–Ņ—Ä—Ź–ľ–ļ—É, –Ņ–ĺ—Ē–ī–Ĺ–į–Ĺ–ĺ–≥–ĺ –∑—Ė —Ā–ļ–Ľ–į–ī–Ĺ—Ė—ą–ł–ľ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–ĺ–ľ –Ľ—Ė–Ĺ—Ė–Ļ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ—ą—É–ļ—É –ī–Ľ—Ź –∑–Ĺ–į—Ö–ĺ–ī–∂–Ķ–Ĺ–Ĺ—Ź ¬ę–Ĺ–į–Ļ–ļ—Ä–į—Č–ĺ–≥–嬼 –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź
γ ő≥ -->
{\displaystyle \gamma }
–ě-–Ď–§–ď–® [en]
–ď—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ –ľ–ĺ–∂–Ķ —Ä–ĺ–∑–≥–Ľ—Ź–ī–į—ā–ł—Ā—Ź —Ź–ļ –ľ–Ķ—ā–ĺ–ī –ē–Ļ–Ľ–Ķ—Ä–į –ī–Ľ—Ź —Ä–ĺ–∑–≤'—Ź–∑–į–Ĺ–Ĺ—Ź –∑–≤–ł—á–į–Ļ–Ĺ–ł—Ö –ī–ł—Ą–Ķ—Ä–Ķ–Ĺ—Ü—Ė–Ļ–Ĺ–ł—Ö —Ä—Ė–≤–Ĺ—Ź–Ĺ—Ć
x
′
(
t
)
=
− ‚ąí -->
∇ ‚ąá -->
f
(
x
(
t
)
)
{\displaystyle x'(t)=-\nabla f(x(t))}
–Ņ–ĺ—ā–ĺ–ļ—É –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–į .
Python
–ź–Ľ–≥–ĺ—Ä–ł—ā–ľ –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ĺ–≥–ĺ —Ā–Ņ—É—Ā–ļ—É –∑–į—Ā—ā–ĺ—Ā–ĺ–≤—É—Ē—ā—Ć—Ā—Ź –ī–Ľ—Ź –∑–Ĺ–į—Ö–ĺ–ī–∂–Ķ–Ĺ–Ĺ—Ź –Ľ–ĺ–ļ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ľ—Ė–Ĺ—Ė–ľ—É–ľ—É —Ą—É–Ĺ–ļ—Ü—Ė—ó f (x )=x 4 ‚ąí3x 3 +2 –∑ –Ņ–ĺ—Ö—Ė–ī–Ĺ–ĺ—é f '(x )=4x 3 ‚ąí9x 2 . –ě—Ā—Ć —Ä–Ķ–į–Ľ—Ė–∑–į—Ü—Ė—Ź –ľ–ĺ–≤–ĺ—é –Ņ—Ä–ĺ–≥—Ä–į–ľ—É–≤–į–Ĺ–Ĺ—Ź Python .
# –í–ł—Ö–ĺ–ī—Ź—á–ł –∑ –ĺ–Ī—á–ł—Ā–Ľ–Ķ–Ĺ—Ć, –ľ–ł –ĺ—á—Ė–ļ—É—Ē–ľ–ĺ, —Č–ĺ –Ľ–ĺ–ļ–į–Ľ—Ć–Ĺ–ł–Ļ –ľ—Ė–Ĺ—Ė–ľ—É–ľ –ľ–į—ā–ł–ľ–Ķ –ľ—Ė—Ā—Ü–Ķ –≤ x=9/4
x_old = 0 # –¶–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź –Ĺ–Ķ –≤–į–∂–Ľ–ł–≤–Ķ, –ĺ—Ā–ļ—Ė–Ľ—Ć–ļ–ł abs(x_new - x_old) > precision
x_new = 6 # –ź–Ľ–≥–ĺ—Ä–ł—ā–ľ —Ā—ā–į—Ä—ā—É—Ē –∑ x=6
gamma = 0.01 # —Ä–ĺ–∑–ľ—Ė—Ä –ļ—Ä–ĺ–ļ—É
precision = 0.00001
def f_derivative ( x ):
return 4 * x ** 3 - 9 * x ** 2
while abs ( x_new - x_old ) > precision :
x_old = x_new
x_new = x_old - gamma * f_derivative ( x_old )
print ( "–õ–ĺ–ļ–į–Ľ—Ć–Ĺ–ł–Ļ –ľ—Ė–Ĺ—Ė–ľ—É–ľ –ľ–į—Ē –ľ—Ė—Ā—Ü–Ķ –≤" , x_new )
–Ě–į–≤–Ķ–ī–Ķ–Ĺ–ł–Ļ –≤–ł—Č–Ķ —Ą—Ä–į–≥–ľ–Ķ–Ĺ—ā –ļ–ĺ–ī—É –ľ–į—Ē –Ī—É—ā–ł –∑–ľ—Ė–Ĺ–Ķ–Ĺ–ĺ –Ņ–ĺ –≤—Ė–ī–Ĺ–ĺ—ą–Ķ–Ĺ–Ĺ—é –ī–ĺ —Ä–ĺ–∑–ľ—Ė—Ä—É –ļ—Ä–ĺ–ļ—É –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–Ĺ–ĺ –ī–ĺ —Ā–ł—Ā—ā–Ķ–ľ–ł, —Ź–ļ–į —Ē –Ņ—Ė–ī —Ä—É–ļ–į–ľ–ł, –į –∑–Ī—Ė–∂–Ĺ—Ė—Ā—ā—Ć –ľ–ĺ–∂–Ķ –Ī—É—ā–ł –∑—Ä–ĺ–Ī–Ľ–Ķ–Ĺ–ĺ —ą–≤–ł–ī—ą–ĺ—é —ą–Ľ—Ź—Ö–ĺ–ľ –∑–į—Ā—ā–ĺ—Ā—É–≤–į–Ĺ–Ĺ—Ź –į–ī–į–Ņ—ā–ł–≤–Ĺ–ĺ–≥–ĺ —Ä–ĺ–∑–ľ—Ė—Ä—É –ļ—Ä–ĺ–ļ—É. –í –Ĺ–į–≤–Ķ–ī–Ķ–Ĺ–ĺ–ľ—É –≤–ł—Č–Ķ –≤–ł–Ņ–į–ī–ļ—É —Ä–ĺ–∑–ľ—Ė—Ä –ļ—Ä–ĺ–ļ—É –Ĺ–Ķ —Ē –į–ī–į–Ņ—ā–ł–≤–Ĺ–ł–ľ. –í—Ė–Ĺ –∑–į–Ľ–ł—ą–į—Ē—ā—Ć—Ā—Ź –Ĺ–į —Ä—Ė–≤–Ĺ—Ė 0.01 –≤ —É—Ā—Ė—Ö –Ĺ–į–Ņ—Ä—Ź–ľ–ļ–į—Ö, —Č–ĺ –ľ–ĺ–∂–Ķ —Ė–Ĺ–ĺ–ī—Ė –Ņ—Ä–ł–∑–≤–ĺ–ī–ł—ā–ł –ī–ĺ –Ĺ–Ķ–≤–ī–į—á—Ė –ľ–Ķ—ā–ĺ–ī—É –∑–į —Ä–į—Ö—É–Ĺ–ĺ–ļ –≤—Ė–ī—Ö–ł–Ľ–Ķ–Ĺ–Ĺ—Ź –≤—Ė–ī –ľ—Ė–Ĺ—Ė–ľ—É–ľ—É.
MATLAB
–Ě–į—Ā—ā—É–Ņ–Ĺ–ł–Ļ –ļ–ĺ–ī MATLAB –ī–Ķ–ľ–ĺ–Ĺ—Ā—ā—Ä—É—Ē –ļ–ĺ–Ĺ–ļ—Ä–Ķ—ā–Ĺ–Ķ —Ä—Ė—ą–Ķ–Ĺ–Ĺ—Ź –ī–Ľ—Ź —Ä–ĺ–∑–≤'—Ź–∑–į–Ĺ–Ĺ—Ź —Ā–ł—Ā—ā–Ķ–ľ–ł –Ĺ–Ķ–Ľ—Ė–Ĺ—Ė–Ļ–Ĺ–ł—Ö —Ä—Ė–≤–Ĺ—Ź–Ĺ—Ć, –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ĺ—ó –≤ –Ņ–ĺ–Ņ–Ķ—Ä–Ķ–ī–Ĺ—Ć–ĺ–ľ—É —Ä–ĺ–∑–ī—Ė–Ľ—Ė :
{
3
x
1
− ‚ąí -->
cos
‚Ā° -->
(
x
2
x
3
)
− ‚ąí -->
3
2
=
0
4
x
1
2
− ‚ąí -->
625
x
2
2
+
2
x
2
− ‚ąí -->
1
=
0
exp
‚Ā° -->
(
− ‚ąí -->
x
1
x
2
)
+
20
x
3
+
10
π ŌÄ -->
− ‚ąí -->
3
3
=
0
{\displaystyle {\begin{cases}3x_{1}-\cos(x_{2}x_{3})-{\tfrac {3}{2}}=0\\4x_{1}^{2}-625x_{2}^{2}+2x_{2}-1=0\\\exp(-x_{1}x_{2})+20x_{3}+{\tfrac {10\pi -3}{3}}=0\end{cases}}}
% –Ď–į–≥–į—ā–ĺ–≤–ł–ľ—Ė—Ä–Ĺ–į –≤–Ķ–ļ—ā–ĺ—Ä-—Ą—É–Ĺ–ļ—Ü—Ė—Ź G(x)
G = @( x ) [
3 * x ( 1 ) - cos ( x ( 2 ) * x ( 3 )) - 3 / 2 ;
4 * x ( 1 ) ^2 - 625 * x ( 2 ) ^2 + 2 * x ( 2 ) - 1 ;
exp ( - x ( 1 ) * x ( 2 )) + 20 * x ( 3 ) + ( 10 * pi - 3 ) / 3 ];
% –Į–ļ–ĺ–Ī—Ė–į–Ĺ G
JG = @( x ) [
3 , sin ( x ( 2 ) * x ( 3 )) * x ( 3 ), sin ( x ( 2 ) * x ( 3 )) * x ( 2 ) ;
8 * x ( 1 ), - 1250 * x ( 2 ) + 2 , 0 ;
- x ( 2 ) * exp ( - x ( 1 ) * x ( 2 )), - x ( 1 ) * exp ( - x ( 1 ) * x ( 2 )), 20 ];
% –¶—Ė–Ľ—Ć–ĺ–≤–į —Ą—É–Ĺ–ļ—Ü—Ė—Ź F(x), —Ź–ļ—É –Ņ–ĺ—ā—Ä—Ė–Ī–Ĺ–ĺ –ľ—Ė–Ĺ—Ė–ľ—Ė–∑—É–≤–į—ā–ł, —Č–ĺ–Ī–ł —Ä–ĺ–∑–≤'—Ź–∑–į—ā–ł G(x)=0
F = @( x ) 0.5 * sum ( G ( x ) .^ 2 );
% –ď—Ä–į–ī—Ė—Ē–Ĺ—ā F (—á–į—Ā—ā–ļ–ĺ–≤—Ė –Ņ–ĺ—Ö—Ė–ī–Ĺ—Ė)
dF = @( x ) JG ( x ). ' * G ( x );
% –ü–į—Ä–į–ľ–Ķ—ā—Ä–ł
GAMMA = 0.001 ; % —Ä–ĺ–∑–ľ—Ė—Ä –ļ—Ä–ĺ–ļ—É (—ā–Ķ–ľ–Ņ –Ĺ–į–≤—á–į–Ĺ–Ĺ—Ź)
MAX_ITER = 1000 ; % –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–Ķ —á–ł—Ā–Ľ–ĺ —Ė—ā–Ķ—Ä–į—Ü—Ė–Ļ
FUNC_TOL = 0.1 ; % –ļ—Ė–Ĺ—Ü–Ķ–≤–Ķ –ī–ĺ–Ņ—É—Ā—ā–ł–ľ–Ķ –≤—Ė–ī—Ö–ł–Ľ–Ķ–Ĺ–Ĺ—Ź F(x)
fvals = []; % –∑–Ī–Ķ—Ä—Ė–≥–į–Ĺ–Ĺ—Ź –∑–Ĺ–į—á–Ķ–Ĺ—Ć F(x) –Ņ—Ä–ĺ—ā—Ź–≥–ĺ–ľ —Ė—ā–Ķ—Ä–į—Ü—Ė–Ļ
progress = @( iter , x ) fprintf ( 'iter = %3d: x = %-32s, F(x) = %f\n' , ...
iter , mat2str ( x , 6 ), F ( x ));
% –Ü—ā–Ķ—Ä—É–≤–į–Ĺ–Ĺ—Ź
iter = 1 ; % –Ľ—Ė—á–ł–Ľ—Ć–Ĺ–ł–ļ —Ė—ā–Ķ—Ä–į—Ü—Ė–Ļ
x = [ 0 ; 0 ; 0 ]; % –Ņ–ĺ—á–į—ā–ļ–ĺ–≤–Ķ –Ņ—Ä–ł–Ņ—É—Č–Ķ–Ĺ–Ĺ—Ź
fvals ( iter ) = F ( x );
progress ( iter , x );
while iter < MAX_ITER && fvals ( end ) > FUNC_TOL
iter = iter + 1 ;
x = x - GAMMA * dF ( x ); % –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ
fvals ( iter ) = F ( x ); % –ĺ–Ī—á–ł—Ā–Ľ–ł—ā–ł —Ü—Ė–Ľ—Ć–ĺ–≤—É —Ą—É–Ĺ–ļ—Ü—Ė—é
progress ( iter , x ); % –Ņ–ĺ–ļ–į–∑–į—ā–ł –Ņ–Ķ—Ä–Ķ–Ī—Ė–≥
end
% –Ě–į–ļ—Ä–Ķ—Ā–Ľ–ł—ā–ł
plot ( 1 : iter , fvals , 'LineWidth' , 2 ); grid on ;
title ( 'Objective Function' ); xlabel ( 'Iteration' ); ylabel ( 'F(x)' );
% –ě–Ī—á–ł—Ā–Ľ–ł—ā–ł –ļ—Ė–Ĺ—Ü–Ķ–≤–ł–Ļ —Ä–ĺ–∑–≤'—Ź–∑–ĺ–ļ —Ā–ł—Ā—ā–Ķ–ľ–ł —Ä—Ė–≤–Ĺ—Ź–Ĺ—Ć G(x)=0
disp ( 'G(x) = ' ); disp ( G ( x ))
% –í–ł–≤–Ķ–ī–Ķ–Ĺ–Ĺ—Ź:
%
% iter = 1: x = [0;0;0] , F(x) = 58.456136
% iter = 2: x = [0.0075;0.002;-0.20944] , F(x) = 23.306394
% iter = 3: x = [0.015005;0.0015482;-0.335103] , F(x) = 10.617030
% ...
% iter = 187: x = [0.683335;0.0388258;-0.52231] , F(x) = 0.101161
% iter = 188: x = [0.684666;0.0389831;-0.522302] , F(x) = 0.099372
%
% (–∑–Ī—Ė–≥–Ľ–ĺ—Ā—Ź –∑–į 188 —Ė—ā–Ķ—Ä–į—Ü—Ė–Ļ –Ņ—Ė—Ā–Ľ—Ź –Ņ–Ķ—Ä–Ķ–≤–ł—Č–Ķ–Ĺ–Ĺ—Ź –ļ—Ė–Ĺ—Ü–Ķ–≤–ĺ–≥–ĺ –ī–ĺ–Ņ—É—Ā—ā–ł–ľ–ĺ–≥–ĺ –≤—Ė–ī—Ö–ł–Ľ–Ķ–Ĺ–Ĺ—Ź F(x))
–ď—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ł–Ļ —Ā–Ņ—É—Ā–ļ –ľ–ĺ–∂–Ķ –Ī—É—ā–ł —Ä–ĺ–∑—ą–ł—Ä–Ķ–Ĺ–ĺ –ī–Ľ—Ź –Ņ—Ė–ī—ā—Ä–ł–ľ–ļ–ł –ĺ–Ī–ľ–Ķ–∂–Ķ–Ĺ—Ć —ą–Ľ—Ź—Ö–ĺ–ľ –≤–ļ–Ľ—é—á–Ķ–Ĺ–Ĺ—Ź –Ņ—Ä–ĺ—Ē–ļ—Ü—Ė—ó –Ĺ–į –ľ–Ĺ–ĺ–∂–ł–Ĺ—É –ĺ–Ī–ľ–Ķ–∂–Ķ–Ĺ—Ć. –¶–Ķ–Ļ –ľ–Ķ—ā–ĺ–ī –Ņ—Ė–ī—Ö–ĺ–ī–ł—ā—Ć –Ľ–ł—ą–Ķ —ā–ĺ–ī—Ė, –ļ–ĺ–Ľ–ł —Ü—Ź –Ņ—Ä–ĺ—Ē–ļ—Ü—Ė—Ź —Ē –Ķ—Ą–Ķ–ļ—ā–ł–≤–Ĺ–ĺ –ĺ–Ī—á–ł—Ā–Ľ—é–≤–į–Ĺ–ĺ—é –Ĺ–į –ļ–ĺ–ľ–Ņ'—é—ā–Ķ—Ä—Ė. –ó–į –∑—Ä—É—á–Ĺ–ł—Ö –Ņ—Ä–ł–Ņ—É—Č–Ķ–Ĺ—Ć —Ü–Ķ–Ļ –ľ–Ķ—ā–ĺ–ī –∑–Ī—Ė–≥–į—Ē—ā—Ć—Ā—Ź. –¶–Ķ–Ļ –ľ–Ķ—ā–ĺ–ī —Ē –ĺ–ļ—Ä–Ķ–ľ–ł–ľ –≤–ł–Ņ–į–ī–ļ–ĺ–ľ –Ņ–ĺ—Ā–Ľ—Ė–ī–ĺ–≤–Ĺ–ĺ-–∑–≤–ĺ—Ä–ĺ—ā–Ĺ–ĺ–≥–ĺ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ—É –ī–Ľ—Ź –ľ–ĺ–Ĺ–ĺ—ā–ĺ–Ĺ–Ĺ–ł—Ö –≤–ļ–Ľ—é—á–Ķ–Ĺ—Ć (—Ź–ļ–ł–Ļ –≤–ļ–Ľ—é—á–į—Ē –ĺ–Ņ—É–ļ–Ľ–Ķ –Ņ—Ä–ĺ–≥—Ä–į–ľ—É–≤–į–Ĺ–Ĺ—Ź —ā–į –≤–į—Ä—Ė–į—Ü—Ė–Ļ–Ĺ—Ė –Ĺ–Ķ—Ä—Ė–≤–Ĺ–ĺ—Ā—ā—Ė [en] [ 6]
–Ü–Ĺ—ą–Ķ —Ä–ĺ–∑—ą–ł—Ä–Ķ–Ĺ–Ĺ—Ź –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ĺ–≥–ĺ —Ā–Ņ—É—Ā–ļ—É –≤–ł–Ĺ–ł–ļ–Ľ–ĺ –∑–į–≤–ī—Ź–ļ–ł –ģ—Ä—Ė—Ē–≤—Ė –Ě–Ķ—Ā—ā–Ķ—Ä–ĺ–≤—É [en] [ 7]
F
{\displaystyle F}
∇ ‚ąá -->
F
{\displaystyle \nabla F}
–Ľ—Ė–Ņ—ą–ł—Ü–Ķ–≤–ĺ—é , —Ė –Ĺ–Ķ–ľ–į—Ē –Ņ—Ä–ł–Ņ—É—Č–Ķ–Ĺ–Ĺ—Ź, —Č–ĺ
F
{\displaystyle F}
—Ā–ł–Ľ—Ć–Ĺ–ĺ –ĺ–Ņ—É–ļ–Ľ–ĺ—é , —ā–ĺ –Ņ–ĺ—Ö–ł–Ī–ļ—É —Ü—Ė–Ľ—Ć–ĺ–≤–ĺ–≥–ĺ –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź, –Ņ–ĺ—Ä–ĺ–ī–∂—É–≤–į–Ĺ—É –ľ–Ķ—ā–ĺ–ī–ĺ–ľ –≥—Ä–į–ī—Ė—Ē–Ĺ—ā–Ĺ–ĺ–≥–ĺ —Ā–Ņ—É—Ā–ļ—É –Ĺ–į –ļ–ĺ–∂–Ĺ–ĺ–ľ—É –ļ—Ä–ĺ—Ü—Ė
k
{\displaystyle k}
–ĺ–Ī–ľ–Ķ–∂–Ķ–Ĺ–ĺ
O
(
1
/
k
)
{\displaystyle {\mathcal {O}}(1/k)}
O
(
1
/
k
2
)
{\displaystyle {\mathcal {O}}(1/k^{2})}
[ 8]
–©–Ķ –ĺ–ī–Ĺ–ł–ľ —Ä–ĺ–∑—ą–ł—Ä–Ķ–Ĺ–Ĺ—Ź–ľ, —Ź–ļ–Ķ –∑–Ĺ–ł–∂—É—Ē —Ä–ł–∑–ł–ļ –∑–į—Ā—ā—Ä—Ź–≥–Ĺ—É—ā–ł –≤ –Ľ–ĺ–ļ–į–Ľ—Ć–Ĺ–ĺ–ľ—É –ľ—Ė–Ĺ—Ė–ľ—É–ľ—Ė, –į —ā–į–ļ–ĺ–∂ —Ė—Ā—ā–ĺ—ā–Ĺ–ĺ –Ņ—Ä–ł—Ā–ļ–ĺ—Ä—é—Ē –∑–Ī—Ė–∂–Ĺ—Ė—Ā—ā—Ć —É –≤–ł–Ņ–į–ī–ļ–į—Ö, –ļ–ĺ–Ľ–ł —Ė–Ĺ–į–ļ—ą–Ķ –Ņ—Ä–ĺ—Ü–Ķ—Ā –Ī–ł —Ā–ł–Ľ—Ć–Ĺ–ĺ –∑–ł“Ď–∑–į“Ď—É–≤–į–≤, —Ē –ľ–Ķ—ā–ĺ–ī —Ė–ľ–Ņ—É–Ľ—Ć—Ā—É (–į–Ĺ–≥–Ľ. momentum method ), —Ź–ļ–ł–Ļ –≤–ł–ļ–ĺ—Ä–ł—Ā—ā–ĺ–≤—É—Ē —á–Ľ–Ķ–Ĺ —Ė–ľ–Ņ—É–Ľ—Ć—Ā—É –Ņ–ĺ –į–Ĺ–į–Ľ–ĺ–≥—Ė—ó –∑ ¬ę–ľ–į—Ā–ĺ—é –Ĺ—Ć—é—ā–ĺ–Ĺ–ĺ–≤–ł—Ö —á–į—Ā—ā–ł–Ĺ–ĺ–ļ, —Ź–ļ—Ė —Ä—É—Ö–į—é—ā—Ć—Ā—Ź –≤'—Ź–∑–ļ–ł–ľ —Ā–Ķ—Ä–Ķ–ī–ĺ–≤–ł—Č–Ķ–ľ —É –ļ–ĺ–Ĺ—Ā–Ķ—Ä–≤–į—ā–ł–≤–Ĺ–ĺ–ľ—É —Ā–ł–Ľ–ĺ–≤–ĺ–ľ—É –Ņ–ĺ–Ľ—Ė¬Ľ.[ 9] –∑–≤–ĺ—Ä–ĺ—ā–Ĺ–ĺ–≥–ĺ –Ņ–ĺ—ą–ł—Ä–Ķ–Ĺ–Ĺ—Ź , —Č–ĺ –∑–į—Ā—ā–ĺ—Ā–ĺ–≤—É—é—ā—Ć—Ā—Ź –ī–Ľ—Ź —ā—Ä–Ķ–Ĺ—É–≤–į–Ĺ–Ĺ—Ź —ą—ā—É—á–Ĺ–ł—Ö –Ĺ–Ķ–Ļ—Ä–ĺ–Ĺ–Ĺ–ł—Ö –ľ–Ķ—Ä–Ķ–∂ .[ 10] [ 11]
‚ÜĎ Kiwiel, Krzysztof C. (2001). Convergence and efficiency of subgradient methods for quasiconvex minimization. Mathematical Programming (Series A) . –Ę. 90, ‚ĄĖ 1. Berlin, Heidelberg: Springer. —Ā. 1‚ÄĒ25. doi :10.1007/PL00011414 . ISSN 0025-5610 . MR 1819784 . (–į–Ĺ–≥–Ľ.) ‚ÜĎ Yuan, Ya-xiang (1999). Step-sizes for the gradient method (PDF) . AMS/IP Studies in Advanced Mathematics . Providence, RI: American Mathematical Society. 42 (2): 785. {{cite journal }}: –ě–Ī—Ā–Ľ—É–≥–ĺ–≤—É–≤–į–Ĺ–Ĺ—Ź CS1: –°—ā–ĺ—Ä—Ė–Ĺ–ļ–ł –∑ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ĺ–ľ url-status, –į–Ľ–Ķ –Ī–Ķ–∑ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–į archive-url (–Ņ–ĺ—Ā–ł–Ľ–į–Ĺ–Ĺ—Ź )(–į–Ĺ–≥–Ľ.) ‚ÜĎ G. P. Akilov, L. V. Kantorovich, Functional Analysis, Pergamon Pr; 2 Sub edition, ISBN 0-08-023036-9 , 1982 (–į–Ĺ–≥–Ľ.)
‚ÜĎ W. H. Press, S. A. Teukolsky, W. T. Vetterling, B. P. Flannery, Numerical Recipes in C: The Art of Scientific Computing , 2nd Ed., Cambridge University Press, New York, 1992 (–į–Ĺ–≥–Ľ.)
‚ÜĎ T. Strutz: Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond). 2nd edition, Springer Vieweg, 2016, ISBN 978-3-658-11455-8 . (–į–Ĺ–≥–Ľ.)
‚ÜĎ P. L. Combettes and J.-C. Pesquet, ¬ęProximal splitting methods in signal processing¬Ľ [–ź—Ä—Ö—Ė–≤–ĺ–≤–į–Ĺ–ĺ 7 –Ľ–ł–Ņ–Ĺ—Ź 2011 —É Wayback Machine .] , in: Fixed-Point Algorithms for Inverse Problems in Science and Engineering , (H. H. Bauschke, R. S. Burachik , P. L. Combettes, V. Elser, D. R. Luke, and H. Wolkowicz, Editors), pp. 185‚ÄĒ212. Springer, New York, 2011. (–į–Ĺ–≥–Ľ.)
‚ÜĎ Yu. Nesterov, ¬ęIntroductory Lectures on Convex Optimization. A Basic Course¬Ľ (Springer, 2004, ISBN 1-4020-7553-7 ) (–į–Ĺ–≥–Ľ.)
‚ÜĎ Fast Gradient Methods [–ź—Ä—Ö—Ė–≤–ĺ–≤–į–Ĺ–ĺ 24 –≥—Ä—É–ī–Ĺ—Ź 2012 —É Wayback Machine .] , lecture notes by Prof. Lieven Vandenberghe for EE236C at UCLA (–į–Ĺ–≥–Ľ.) ‚ÜĎ Qian, Ning (January 1999). On the momentum term in gradient descent learning algorithms (PDF) . Neural Networks [en] 12 (1): 145‚ÄĒ151. –ź—Ä—Ö—Ė–≤ –ĺ—Ä–ł–≥—Ė–Ĺ–į–Ľ—É (PDF) –∑–į 8 —ā—Ä–į–≤–Ĺ—Ź 2014. –ü—Ä–ĺ—Ü–ł—ā–ĺ–≤–į–Ĺ–ĺ 17 –∂–ĺ–≤—ā–Ĺ—Ź 2014 . (–į–Ĺ–≥–Ľ.) ‚ÜĎ Momentum and Learning Rate Adaptation . Willamette University [en] –ĺ—Ä–ł–≥—Ė–Ĺ–į–Ľ—É –∑–į 21 –∂–ĺ–≤—ā–Ĺ—Ź 2014. –ü—Ä–ĺ—Ü–ł—ā–ĺ–≤–į–Ĺ–ĺ 17 –∂–ĺ–≤—ā–Ĺ—Ź 2014 .(–į–Ĺ–≥–Ľ.) ‚ÜĎ Geoffrey Hinton ; Nitish Srivastava; Kevin Swersky. 6 ‚ÄĒ 3 ‚ÄĒ The momentum method . YouTube –ĺ—Ä–ł–≥—Ė–Ĺ–į–Ľ—É –∑–į 10 —ā—Ä–į–≤–Ĺ—Ź 2015. –ü—Ä–ĺ—Ü–ł—ā–ĺ–≤–į–Ĺ–ĺ 18 –∂–ĺ–≤—ā–Ĺ—Ź 2014 .Coursera Neural Networks for Machine Learning [–ź—Ä—Ö—Ė–≤–ĺ–≤–į–Ĺ–ĺ 29 —á–Ķ—Ä–≤–Ĺ—Ź 2016 —É Wayback Machine .] . (–į–Ĺ–≥–Ľ.)
Mordecai Avriel (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0 . (–į–Ĺ–≥–Ľ.)
Jan A. Snyman (2005). Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms. Springer Publishing. ISBN 0-387-24348-8 (–į–Ĺ–≥–Ľ.)
Raad Z. Homod, K. S. M. Sahari, H. A.F. Almurib, F. H. Nagi, Gradient auto-tuned Takagi-Sugeno fuzzy forward control of a HVAC system using predicted mean vote index Energy and Buildings, 49 (6) (2012) 254‚ÄĒ267 [–ź—Ä—Ö—Ė–≤–ĺ–≤–į–Ĺ–ĺ 11 –≥—Ä—É–ī–Ĺ—Ź 2018 —É Wayback Machine .] (–į–Ĺ–≥–Ľ.)
Cauchy, Augustin (1847). M√©thode g√©n√©rale pour la r√©solution des syst√®mes d'√©quations simultan√©es –ĺ—Ä–ł–≥—Ė–Ĺ–į–Ľ—É –∑–į 13 –∂–ĺ–≤—ā–Ĺ—Ź 2016. –ü—Ä–ĺ—Ü–ł—ā–ĺ–≤–į–Ĺ–ĺ 31 –Ľ–ł–Ņ–Ĺ—Ź 2016 .(—Ą—Ä.) –ē–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī—Ė—Ź –ļ—Ė–Ī–Ķ—Ä–Ĺ–Ķ—ā–ł–ļ–ł : —É 2 —ā. / –∑–į —Ä–Ķ–ī. –í. –ú. –ď–Ľ—É—ą–ļ–ĺ–≤–į . ‚ÄĒ –ö–ł—ó–≤ : –ď–ĺ–Ľ. —Ä–Ķ–ī. –£–ļ—Ä–į—ó–Ĺ—Ā—Ć–ļ–ĺ—ó —Ä–į–ī—Ź–Ĺ—Ā—Ć–ļ–ĺ—ó –Ķ–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī—Ė—ó , 1973.–ü–ĺ–Ľ—Ź–ļ –†. –ź. , –ü—Ä–ł–ľ–į–ļ –ú. –ē. , —ā. 2 , —Ā—ā. 64.
–Ē–ł—Ą–Ķ—Ä–Ķ–Ĺ—Ü—Ė–Ļ–ĺ–≤–Ĺ—Ė –ĺ–Ī—á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ—Ź
–ó–į–≥–į–Ľ—Ć–Ĺ–Ķ –ü–ĺ–Ĺ—Ź—ā—ā—Ź –ú–ĺ–≤–ł –Ņ—Ä–ĺ–≥—Ä–į–ľ—É–≤–į–Ĺ–Ĺ—Ź –ó–į—Ā—ā–ĺ—Ā—É–≤–į–Ĺ–Ĺ—Ź –ź–Ņ–į—Ä–į—ā–Ĺ–Ķ –∑–į–Ī–Ķ–∑–Ņ–Ķ—á–Ķ–Ĺ–Ĺ—Ź –ü—Ä–ĺ–≥—Ä–į–ľ–Ĺ—Ė –Ī—Ė–Ī–Ľ—Ė–ĺ—ā–Ķ–ļ–ł –í—ā—Ė–Ľ–Ķ–Ĺ–Ĺ—Ź
–ź—É–ī—Ė–ĺ–≤—Ė–∑—É–į–Ľ—Ć–Ĺ—Ė –°–Ľ–ĺ–≤–Ķ—Ā–Ĺ—Ė –í–ł—Ä—Ė—ą—É–≤–į–Ľ—Ć–Ĺ—Ė
–õ—é–ī–ł –ě—Ä–≥–į–Ĺ—Ė–∑–į—Ü—Ė—ó