ذ’ذ»ذ°رپر‚ذ¸ذ²ر–رپر‚رŒ رپذ؛ر–ذ½ر‡ذµذ½ذ½ذ¾ذ³ذ¾ ذ؟ذµر€ذµر‚ذ¸ذ½رƒ
|
Read other articles:

Salter Grove Memorial Park breakwater, with Rock Island at the far end Rock Island is an island in Narragansett Bay in the U.S. state of Rhode Island. Rock Island is a small rocky island near Pawtuxet Village and is now connected to the mainland by a causeway. The island is part of the Salter Grove public picnic ground and is the site for a proposed man-made salt marsh using dredged materials. The island contains several unusual fossils. References Narragansett Bay: A Friend's Perspective Fre...

Voce principale: Dipartimento di Stato degli Stati Uniti d'America. Segretario di Stato degli Stati Uniti d'America L'attuale segretario, Antony Blinken Nome originaleUnited States Secretary of State Stato Stati Uniti TipoCapo del Dipartimento di Stato e ministro degli affari esteri In caricaTony Blinken (D) da26 gennaio 2021 Istituito27 luglio 1789 Operativo dal1789 Nominato daPresidente degli Stati Uniti d'America Durata mandato4 anni Sito webwww.state.gov/secretary/index.htm e www.st...

Voce principale: Giochi della XX Olimpiade. Canoa/kayak a Monaco di Baviera 1972 Velocitأ K1 500 m donne K2 500 m donne K1 1000 m uomini K2 1000 m uomini K4 1000 m uomini C1 1000 m uomini C2 1000 m uomini Slalom K1 uomini donne C1 uomini C2 uomini Si sono svolte 11 gare di canoa/kayak alle olimpiadi estive 1972, 7 in acque libere (5 maschili e 2 femminili), presso il Regattastrecke Oberschleiأںheim di Oberschleiأںheim e per la prima volta nelle storia delle olimpiadi, 4 gare di slalom (3 ma...

è؟™وک¯é©¬و¥و—ڈن؛؛هگچ,“èژ«ه“ˆوœ«آ·é›…è¾›â€وک¯çˆ¶هگچ,ن¸چوک¯ه§“و°ڈ,وڈگهڈٹو¤ن؛؛و—¶ه؛”ن»¥ه…¶è‡ھè؛«çڑ„هگچ“و…•ه°¤ن¸پâ€ن¸؛ن¸»م€‚ ه°ٹو•¬çڑ„ن¸¹و–¯é‡Œو‹؟ç£ه“ˆèٹو…•ه°¤ن¸پآ·èژ«ه“ˆوœ«é›…辛馬ن¾†èھï¼ڑMuhyiddin Mohd YassinMahiaddin bin Md Yasin(و³¨ه†Œهگچ)ه›½ن¼ڑè®®ه‘کPSM; SPMJ; SHMS; SPSA; SPMP; SUNS; SPDK; DP; PNBS; SMJ; BSI (I); PIS (I)2021ه¹´çڑ„و…•ه°¤ن¸پ 第8ن»»é©¬و¥è¥؟ن؛ڑ首相ن»»وœں2020ه¹´3وœˆ1و—¥â€”2021ه¹´8وœˆ20و—¥هگ›ن¸»هœ‹ه®¶ه…ƒé¦–èک‡ن¸¹éک؟都و‹‰ه‰¯èپŒن¾و–¯è؟ˆو²™و¯”里ه‰چن»»é©¬...

Antoine de Caunes presentatore della cerimonia La cerimonia di premiazione della 36آھ edizione dei Premi Cأ©sar si أ¨ svolta il 25 febbraio 2011 al Thأ©أ¢tre du Chأ¢telet di Parigi. أˆ stata presieduta da Jodie Foster e presentata da Antoine de Caunes. أˆ stata trasmessa da Canal+.[1] Le candidature sono state rese note il 21 gennaio 2011.[1] Ad ottenerne il maggior numero (undici) أ¨ stato Uomini di Dio (Des hommes et des dieux) di Xavier Beauvois. Nel corso della cerimonia ï؟½...
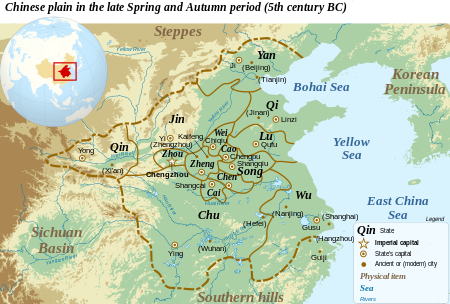
LuDati amministrativiPoliticaTerritorio e popolazioneLo stato di Lu e gli altri Regni durante il periodo delle primavere e degli autunni. Evoluzione storicaOra parte di Cina Modifica dati su Wikidata آ· Manuale Lo stato di Lu (é¯T, Lا”P) fu un antico Stato cinese durante il Periodo delle primavere e degli autunni. Fu fondato nel X secolo a.C. dalla famiglia Ji. Il primo duca fu Ji Boqin, figlio di Ji Dan, primo ministro del re Zhou. Il territorio dello Stato di Lu copriva la re...

و›؟ن»£éکµç؛؟Alternative Front Barisan Alternatifமாறà¯چà®±à¯پ à®®à¯پனà¯چனணà®؟简称BAم€پو›؟éکµوˆگç«‹1998ه¹´9وœˆ20و—¥ (1998-09-20)设立(وœھو£ه¼ڈو³¨ه†Œï¼‰è§£و•£2008ه¹´3وœˆ31و—¥ (2008-03-31)ه‰چè؛« 穆و–¯و—ه›¢ç»“éکµç؛؟(APU) ن؛؛و°‘éکµç؛؟(GR)继و‰؟者ن؛؛و°‘èپ”ç›ں(PR)و€»éƒ¨ه…«و‰“çپµه†چن¹ں(ن؛؛و°‘ه…¬و£ه…ڑ) 黑é£ژو´é•‡(马و¥è¥؟ن؛ڑن؛؛و°‘ه…ڑ) هگ‰éڑ†ه،(و°‘ن¸»è،Œهٹ¨ه…ڑه’Œن¼ٹو–¯ه…°ه…ڑ)ه…ڑوٹ¥م€ٹه…¬و£ن¹‹ه£°ï¼ˆé¦¬ن¾†èھï¼ڑSuara Keadilan)م€‹م€ٹçپ«ç®وٹ¥ï¼ˆé¦¬...

2016ه¹´ç¾ژهœ‹ç¸½çµ±éپ¸èˆ‰ ← 2012 2016ه¹´11وœˆ8و—¥ 2020 → 538ه€‹éپ¸èˆ‰ن؛؛هœکه¸ن½چçچ²ه‹éœ€270票و°‘و„ڈèھ؟وں¥وٹ•ç¥¨çژ‡55.7%[1][2] â–² 0.8 % èژ·وڈگهگچن؛؛ ه”گç´چآ·ه·و™® ه¸Œو‹‰èژ‰آ·ه…‹و—é “ و”؟ه…ڑ ه…±ه’Œé»¨ و°‘ن¸»ه…ڑ ه®¶é„‰ه· ç´گç´„ه· ç´گç´„ه· ç«é€‰وگو،£ è؟ˆه…‹آ·ه½و–¯ è’‚ه§†آ·ه‡±وپ© 选ن¸¾ن؛؛票 304[3][4][註 1] 227[5] 胜ه‡؛ه·/çœپ 30 + ç·¬-2 20 + DC و°‘éپ¸ه¾—票 62,984,828[6] 65,853,514[6]...
2020ه¹´ه¤ڈه£ه¥¥و—هŒ¹ه…‹è؟گهٹ¨ن¼ڑو³¢ه…°ن»£è،¨هœکو³¢ه…°ه›½و——IOC編碼POLNOCو³¢èکه¥§و—هŒ¹ه…‹ه§”ه“،وœƒç¶²ç«™olimpijski.pl(英و–‡ï¼‰ï¼ˆو³¢ه…°و–‡ï¼‰2020ه¹´ه¤ڈه£ه¥¥و—هŒ¹ه…‹è؟گهٹ¨ن¼ڑ(و±ن؛¬ï¼‰2021ه¹´7وœˆ23و—¥è‡³8وœˆ8و—¥ï¼ˆهڈ—2019ه† çٹ¶ç—…و¯’ç—…ç–«وƒ…ه½±ه“چوژ¨è؟ں,ن½†ن»چن؟ç•™هژںه®ڑهگچ称)éپ‹ه‹•ه“،206هڈƒè³½é …ç›®24ن¸ھه¤§é،¹و——و‰‹ه¼€ه¹•ه¼ڈï¼ڑه¸•ç»´ه°”آ·ç§‘çƒه°¼ه¥¥ه¤«و–¯هں؛(و¸¸و³³ï¼‰ه’Œé©¬ه¨…آ·و²ƒن»€ن¹”ه¤«و–¯هچ،(è‡ھè،Œè½¦ï¼‰[1]é—ه¹•ه¼ڈï¼ڑهچ،ç½—هˆ©ه¨œآ·ç؛³ن؛ڑ(çڑ®هˆ’艇)&#...

ظ‡ط°ظ‡ ط§ظ„ظ…ظ‚ط§ظ„ط© طھططھط§ط¬ ظ„ظ„ظ…ط²ظٹط¯ ظ…ظ† ط§ظ„ظˆطµظ„ط§طھ ظ„ظ„ظ…ظ‚ط§ظ„ط§طھ ط§ظ„ط£ط®ط±ظ‰ ظ„ظ„ظ…ط³ط§ط¹ط¯ط© ظپظٹ طھط±ط§ط¨ط· ظ…ظ‚ط§ظ„ط§طھ ط§ظ„ظ…ظˆط³ظˆط¹ط©. ظپط¶ظ„ظ‹ط§ ط³ط§ط¹ط¯ ظپظٹ طھطط³ظٹظ† ظ‡ط°ظ‡ ط§ظ„ظ…ظ‚ط§ظ„ط© ط¨ط¥ط¶ط§ظپط© ظˆطµظ„ط§طھ ط¥ظ„ظ‰ ط§ظ„ظ…ظ‚ط§ظ„ط§طھ ط§ظ„ظ…طھط¹ظ„ظ‚ط© ط¨ظ‡ط§ ط§ظ„ظ…ظˆط¬ظˆط¯ط© ظپظٹ ط§ظ„ظ†طµ ط§ظ„طط§ظ„ظٹ. (ظ…ط§ط±ط³ 2018) ظ…ظ‚ط§ط·ط¹ط© ط£ظ„ط¨ط§ظٹظ† ط¹ظ„ظ… ط§ظ„ط¥طط¯ط§ط«ظٹط§طھ 38آ°35′N 119آ°48′W / 38.58آ°N 119.8آ°W / 38....

Virtuoso lead guitar solo playing style Joe Satriani, Steve Vai and John Petrucci at the G3 (tour) in December 2006 Shred guitar is a virtuosic style of electric guitar performance. Categorized by its use of advanced techniques, shredding is a complex art form. Shred guitar includes fast alternate picking, sweep-picking, diminished and harmonic minor scales, tapping, and whammy bar use.[1] Often incorporated in heavy metal, guitarists employ a guitar amplifier and a range of effects s...

American mountain range This article is about the northernmost extent of the greater Sangre de Cristo mountain range. For the full extent of the mountain range, see Sangre de Cristo Mountains. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sangre de Cristo Range – news آ· newspapers آ· books آ· scholar آ· JSTOR...

هŒ—وµ·ه„ھé§؟ 第43ه›هŒ—وµ·ه„ھé§؟مپ®ه„ھه‹مƒ¬م‚¤مپ¨é¦¬ç€م‚’ç€è£…مپ—مپںه‹هˆ©é¦¬مƒ•م‚¸مƒژم‚µمƒ مƒ©م‚¤é–‹ه‚¬ه›½ و—¥وœ¬ن¸»ه‚¬è€… هŒ—وµ·éپ“競馬ه ´ é–€هˆ¥ç«¶é¦¬ه ´ç¬¬1ه›و–½è،Œو—¥ 1973ه¹´9وœˆ9و—¥2024ه¹´مپ®وƒ…ه ±è·é›¢ مƒ€مƒ¼مƒˆ2000mو ¼ن»کمپ‘ H1è³é‡‘ 1ç€è³é‡‘1500ن¸‡ه††ه‡؛èµ°و،ن»¶ م‚µمƒ©مƒ–مƒ¬مƒƒمƒ‰ç³»3و³ï¼ˆهœ°و–¹ه…¨ه›½ن؛¤وµپï¼‰è² و‹…é‡چé‡ڈ ه®ڑé‡ڈ(57kgم€پç‰2kgو¸›ï¼‰ه‡؛ه…¸ [1]مƒ†مƒ³مƒ—مƒ¬مƒ¼مƒˆم‚’è،¨ç¤؛ هŒ—وµ·ه„ھé§؟(مپ»مپ£مپ‹مپ„م‚†مپ†مپ—م‚…م‚“)مپ¯م€پمƒ›مƒƒم‚«م‚¤مƒ‰م‚¦ç«¶é¦¬مپ§...

Ne doit pas أھtre confondu avec Championnat d'Inde de football 2017-2018. Indian Super League Saison 2017-2018 Gأ©nأ©ralitأ©s Sport Football Organisateur(s) Indian Super League أ‰dition 4e Lieu(x) Inde Date Saison rأ©guliأ¨re :17 novembre 2017 - 4 mars 2018Sأ©ries أ©liminatoires :11 - 17 mars 2018 Nations 1 Participants 10 أ©quipes Disciplines 1 أ‰preuves 95 matchs Site web officiel www.indiansuperleague.com Palmarأ¨s Vainqueur Chennaiyin FC (2e titre) Finaliste Bengaluru FC Meille...

Parliament in revolutionary Ireland (1919-1922) This article is about Dأ،il أ‰ireann as it existed from 1919–1922. For the current parliament, see Dأ،il أ‰ireann. For the other historical legislature, see Dأ،il أ‰ireann (Irish Free State). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Dأ،il أ‰ireann Irish Republic – news&#...

Defensive tower This article is about the defensive tower in a castle wall. For the siege engine sometimes called a battery-tower, see Siege tower. Battery tower of Kufstein Fortress A battery tower was a defensive tower built into the outermost defences of many castles, usually in the 16th century or later, after the advent of firearms. Its name is derived from the word battery, a group of several cannon. These, usually round, towers could house numerous cannon oriented in various directions...

2015 American filmA Dog Named GucciposterDirected byGorman BechardProduced byGorman BechardKristine BechardCinematographyGorman BechardSarah HajtolEdited byGorman BechardMusic byDean FalconeProductioncompanyWhat Were We Thinking FilmsDistributed byMVD EntertainmentRelease date February 14, 2015 (2015-02-14) (Big Sky Documentary Film Festival) Running time84 minutesCountryUnited StatesLanguageEnglish A Dog Named Gucci is a 2015 documentary film by Gorman Bechard that chronic...

1968 film by Antonio Isasi-Isasmendi They Came to Rob Las VegasTheatrical release posterDirected byAntonio IsasiScreenplay by Antonio Isasi Lluis Josep Comeron Jorge Illa Jo Eisinger Based onthe novel Les Hommes De Las Vegasby Andrأ© LayProduced byNat WachsbergerAntonio IsasiStarring Gary Lockwood Elke Sommer Lee J. Cobb Jack Palance CinematographyJuan GelpأEdited byEmilio RodrأguezMusic byGeorges GarvarentzDistributed byWarner Bros.-Seven Arts (United States)Release dates October 31,&...

Cet article est une أ©bauche concernant la Finlande. Vous pouvez partager vos connaissances en l’amأ©liorant (comment ?) selon les recommandations des projets correspondants. Chronologies Donnأ©es clأ©s 1925 1926 1927 1928 1929 1930 1931Dأ©cennies :1890 1900 1910 1920 1930 1940 1950Siأ¨cles :XVIIIe XIXe XXe XXIe XXIIeMillأ©naires :-Ier Ier IIe IIIe Chronologies gأ©ographiques Afrique Afrique du Sud, Algأ©rie, Angola, Bأ©ni...

Cet article est une أ©bauche concernant une unitأ© ou formation militaire franأ§aise. Vous pouvez partager vos connaissances en l’amأ©liorant (comment ?) selon les recommandations des projets correspondants. 370e rأ©giment d'infanterie Sous-officiers du 370e RI dans le Soissonnais en 1917. Crأ©ation aoأ»t 1914 Dissolution 30 octobre 1917 Pays France Branche Armأ©e de terre Type Rأ©giment d'infanterie Rأ´le Infanterie Guerres Premiأ¨re Guerre mondiale modifier Le 370e&#...




