Den här artikeln behöver källhänvisningar för att kunna verifieras. (2016-10) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan.

Inom matematiken är en kontinuerlig funktion en funktion som inte gör några plötsliga hopp och inte har några avbrott, så att nästan lika värden in garanterar nästan lika värden ut. För en reellvärd funktion f med ett reellt argument kan man precisera detta som att man för varje givet reellt tal x₀ där funktionen är definierad och varje given noggrannhet kan vara säker på att f(x) approximerar f(x₀) med minst denna noggrannhet för alla x som ligger tillräckligt nära x₀.

Begreppet kontinuitet är dock mycket använt inom olika delar av matematiken, även sådana där denna intuitiva förklaring inte så lätt låter sig omformuleras i en stringent definition. Topologi är den gren av matematiken som studerar kontinuerliga funktioner i dess mest generella betydelse. Där definieras en funktion mellan två topologiska rum som kontinuerlig, om varje urbild av en öppen mängd är öppen. Man kan visa att denna generella definition betyder samma sak som den vanliga definitionen för "vanliga" funktioner.

• En funktion f definierad på en delmängd av de reella talen är kontinuerlig i en punkt x = x₀ i funktionens definitionsmängd D_f om den där identisk med sitt gränsvärde, det vill säga om

${\displaystyle \lim _{x\rightarrow x_{0}}f(x)=f(x_{0})}$

Att f är kontinuerlig betyder att den är kontinuerlig i varje punkt i D_f. Exempelvis är f definierad av f(x) = 1/x för alla x skilda från 0 kontinuerlig, trots att dess graf "hoppar" i punkten 0.

Den intuitiva beskrivningen med hjälp av "noggrannhet" brukar traditionellt formaliseras i termer av ε (som uttalas epsilon och här betecknar "utvärdesnoggrannheten") och δ (delta, "invärdesnoggrannheten"). Detta ger följande precisa definition i det mest grundläggande fallet.

En reellvärd funktion f av en reell variabel (alltså sådan att dess definitionsmängd D_f ⊆ R) är:

• kontinuerlig i punkten x ∈ D_f om det för vart ε > 0 existerar ett δ > 0 sådant att y ∈ D_f och |x - y| < δ medför |f(x) - f(y)| < ε.
• kontinuerlig i ett intervall (exempelvis [a, b] eller ]a, b[) om den är kontinuerlig i alla punkter i intervallet.
• kontinuerlig om den är kontinuerlig i varje punkt x i D_f.

Man kan göra liknande definitioner exempelvis för funktioner mellan delmängder av olika ändligtdimensionella reella vektorrum, så snart man har preciserat vad |x - y| betyder. Exempelvis brukar man på Rⁿ definiera detta som det euklidiska avståndet:

${\displaystyle |(x_{1},...,x_{n})\;-\;(y_{1},...,y_{n})|={\sqrt {(x_{1}-y_{1})^{2}+...+(x_{n}-y_{n})^{2}}}}$.

Allmännare räcker det om både definitionsmängden och målmängden är försedda med metriker, avståndsfunktioner som uppfyller triangelolikheten. Med andra ord, om (X, d_x) och (Y, d_y) är metriska rum är funktionen f : X → Y kontinuerlig i x ∈ X om det för varje ε > 0 existerar ett δ > 0 så att d_X(x, y) < δ ⇒ d_Y(f(x), f(y)) < ε.

Om X ⊆ R och Y = R ges den vanliga metriken d_R definierad genom d_R(a,b) = |a - b|, är denna definition ekvivalent med den förra definitionen.

För allmänna topologiska rum X och Y gäller att en funktion f : X → Y är kontinuerlig om urbilden av varje öppen mängd i Y är öppen i X. Det vill säga för varje öppen mängd U ⊆ Y gäller att f ^-1(U) är öppen i X.

Man säger att f är kontinuerlig i punkten x om det för varje omgivning V till f(x) finns en omgivning U till x, sådan att f(U) ⊆ V. Om X och Y är metriska rum, så är denna definition ekvivalent med den klassiska ε-och-δ-definitionen.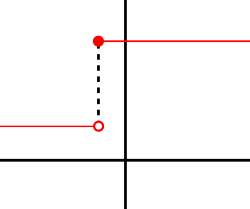

En funktion kan vara kontinuerlig i endast en riktning.

• Differentierbarhet
• Diskret funktion
• Kontinuum
• Lipschitz-kontinuitet
• Likformig kontinuitet

• Wikimedia Commons har media som rör Kontinuerlig funktion.
  Bilder & media