Read other articles:

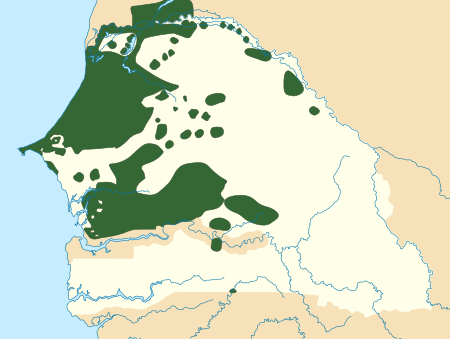
ولوفية الاسم الذاتي (بالولوفية: Wolof)‏    الناطقون 3700000   الكتابة إخطاطة لاتينية،  وأبجدية عربية،  وخط ولوفي  النسب لغات نيجرية كنغوية لغات نيجرية كنغويةالأطلسي والكونغولغات أطلانتيةلغات سنغامبيةالولوفية أيزو 639-1 wo  أيزو 639-2 wol  أيزو 639-3 wol  تعديل مصدري ...

Bodyguard Ugal-ugalanSutradaraIrham Acho BahtiarProduserDhamoo PunjabiChand Parwez ServiaFlaz ServiaGope T. SamtaniDitulis olehFerdy KPemeranSyahriniTamara BleszynskiBoris BokirMuhadkly AchoLoloxAnyun CadelMelayu Nicole HallRirin EkawatiPenata musikIndra QPerusahaanproduksiMD PicturesKharisma Starvision PlusRapi FilmsHOOQDistributorIflix OriginalsTanggal rilis5 Juli 2018Negara IndonesiaBahasaIndonesiaPrekuelSecurity Ugal-ugalan Bodyguard Ugal-ugalan adalah film komedi Indonesia yan...

تراكتور الاسم الكامل نادي تراكتور تبريز اللقب الذئاب الحمراء تأسس عام 1970 الملعب ملعب يادغار إمام[1] تبريز(السعة: 70,000) البلد إيران  الدوري دوري المحترفين الإيراني 2017-18 العاشر الإدارة المالك شركة تراكتورسازي والحرس الثوري[2] الرئيس محمد حسين جعفري المدير الفني جان...

العلاقات الصومالية الصينية الصومال الصين   الصومال   الصين تعديل مصدري - تعديل   العلاقات الصومالية الصينية هي العلاقات الثنائية التي تجمع بين الصومال والصين.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة الص�...

2013 French filmUnder the RainbowFilm posterFrenchAu bout du conte Directed byAgnès JaouiWritten byJean-Pierre BacriAgnès JaouiProduced byAlexandre Mallet-GuyStarringJean-Pierre BacriAgnès JaouiAgathe BonitzerBenjamin BiolayCinematographyLubomir BakchevEdited byFabrice RouaudMusic byFernando FiszbeinProductioncompaniesLa CinéfactureLes Films A4France 2 CinémaMemento Films ProductionDistributed byMemento FilmsRelease dates 14 February 2013 (2013-02-14) (Lyon) 6 Mar...

Flavius Claudius Julianus Nama dalam bahasa asli(la) Flavius Claudius Iulianus BiografiKelahiran17 November 331 Konstantinopel Kematian26 Juni 363 (31 tahun)Mesopotamia Penyebab kematianTerbunuh dalam tugas Tempat pemakamanTarsus Galat: Kedua parameter tahun harus terisi! Konsul Romawi 363 – Juni 363 (kematian) Bersama dengan: Flavius Sallustius Tribunicia potestas Februari 360 –  (masa kerja) Pontifex Maximus Februari 360 – Juni 363 Augustus Februari 360 �...

Serbian footballer Mihajlo Cakić Cakić with Zorya in 2011Personal informationFull name Mihajlo CakićDate of birth (1990-05-27) 27 May 1990 (age 33)Place of birth Leskovac, SFR YugoslaviaHeight 1.82 m (6 ft 0 in)Position(s) MidfielderYouth career Rad Red Star PartizanSenior career*Years Team Apps (Gls)2008–2010 Zemun 26 (1)2010 Čukarički 11 (3)2011–2014 Zorya Luhansk 14 (0)2012–2013 → Slavia Mozyr (loan) 33 (0)2014 OFK Beograd 2 (0)2015 Tiraspol 10 (0)2015 Sher...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。（このテンプレートの使い方）出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL（2017年4月） コルクを打ち抜いて作った瓶の栓 コルク（木栓、�...

Cet article est une ébauche concernant le catholicisme. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Chronologies Données clés 1930 1931 1932  1933  1934 1935 1936Décennies :1900 1910 1920  1930  1940 1950 1960Siècles :XVIIIe XIXe  XXe  XXIe XXIIeMillénaires :-Ier Ier  IIe  IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, B...

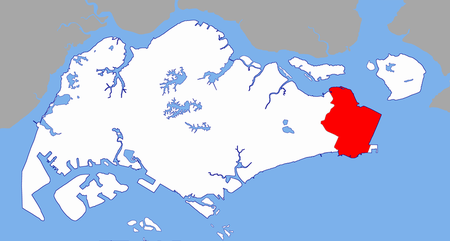
Untuk bandar udara bernama Changi, lihat Bandara Internasional Changi Singapura. ChangiMatahari terbenam di Pantai ChangiInggrisChangiTionghoa樟宜– PinyinZhāngyíMelayuChangiTamilசாங்கி Changi adalah sebuah distrik di sebelah timur Singapura. Berbatasan dengan Pasir Ris dan Tampines di sebelah barat dan Changi Bay di sebelah timur. Changi, yang termasuk salah satu dari dua tempat penyangga air di pulau Singapura, adalah distrik terbesar di negara ini berdasarkan luas...

Swiss equestrian Markus FuchsMarkus Fuchs in 2009Personal informationBorn23 June 1955 (1955-06-23) (age 68) Medal record Representing  Switzerland Equestrian Olympic Games 2000 Sydney Team jumping Markus Fuchs (born 23 June 1955[1] in Abtwil, Switzerland)[citation needed] is a Swiss show jumper who competed at five Olympics between 1988 and 2004. He was part of the Swiss team that won silver at the 2000 Olympics. He is, jointly with shooter Gabriele Bühlmann, t...

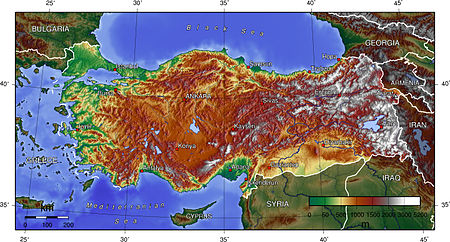
جغرافيا تركيامعلومات عامةالبلد تركيا المنطقة غرب آسيا وجنوب شرق أوروباالقارة آسيا وأوروباالساحل 7,200 كمالحدود مجموع الحدود: 2648 كم أرمينيا 268 كم أذربيجان 9 كم بلغاريا 240 كم Georgia 252 كم, اليونان 206 كم, إيران 499 كم, العراق 352 كم, سوريا 822 كمالإحداثيات 39°00′N 35°...

Untuk kegunaan lain, lihat Tanjungpura. Keraton Kerajaan Tanjungpura Kerajaan Tanjungpura atau Tanjompura[1] merupakan tertua di Kalimantan Barat yang telah wujud sejak abad ke-8. Kerajaan ini mengalami beberapa kali perpindahan ibu kota kerajaan, pertama kali terletak di Negeri Baru (nama desa saat ini) Kabupaten Ketapang, kemudian pindah ke Sukadana (saat ini ibu kota Kabupaten Kayong Utara) pada abad ke-14 M, sejak Rajanya Sorgi (Giri Kesuma) memeluk Islam. Kerajaan Tanjungpura men...

Nilpotent subalgebra of a Lie algebra Lie groups and Lie algebras Classical groups General linear GL(n) Special linear SL(n) Orthogonal O(n) Special orthogonal SO(n) Unitary U(n) Special unitary SU(n) Symplectic Sp(n) Simple Lie groups Classical An Bn Cn Dn Exceptional G2 F4 E6 E7 E8 Other Lie groups Circle Lorentz Poincaré Conformal group Diffeomorphism Loop Euclidean Lie algebras Lie group–Lie algebra correspondence Exponential map Adjoint representation Killing formIndex Simple Lie alge...

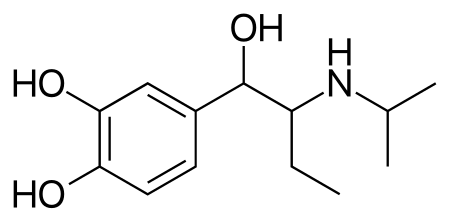
Chemical compound This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Isoetarine – news · newspapers · books · scholar · JSTOR (January 2011) (Learn how and when to remove this message) IsoetharineClinical dataPronunciation/aɪsoʊˈɛθəriːn/ eye-soh-ETH-ə-reen Trade namesBronkosol and Bronkometer (USAN...

The city of The Hague, Netherlands, consists of eight districts (stadsdelen, singular stadsdeel), similar to boroughs. Each district is divided into subdistricts (wijken). Each of these stadsdelen has its own district office (stadsdeelkantoor), where most of the local government activity is organised. These stadsdeelkantoren make many aspects of local government more accessible to residents. The current division of The Hague into individual stadsdelen was created in 1988 by the main city gov...

Head of state of Germany This article is about the position of president of Germany in the current Federal Republic of Germany. For the position of president of Germany in the Weimar Republic, see President of Germany (1919–1945). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: President of Germany – news · newspapers ...

Genus of liverworts Riella Scientific classification Kingdom: Plantae Division: Marchantiophyta Class: Marchantiopsida Order: Sphaerocarpales Family: Riellaceae Genus: RiellaMont. 1852[1] Species See classification Synonyms[2] Duriaea Bory De St. Vincent & Montagne 1843 Duriella Bory de St. Vincent ex Billot 1861 non Row 1911 non Dhanam & Jairajpuri 1999 Maisonneuvea Trevisan 1877 (Trabutiella) Porsild 1902 non Stevens 1920 non Theissen & Sydow 1914 Riella is a gen...

2009 studio album by Charlie HunterGentlemen, I Neglected to Inform You You Will Not Be Getting PaidStudio album by Charlie HunterReleased2009StudioBrooklyn RecordingGenreJazz, jazz rock, jazz fusion, bluesLength37:38LabelSpire/reapandsowProducerCharlie HunterCharlie Hunter chronology Baboon Strength(2008) Gentlemen, I Neglected to Inform You You Will Not Be Getting Paid(2009) Public Domain(2010) Professional ratingsReview scoresSourceRatingAllMusic [1] Gentlemen, I Neglected ...

Questa voce o sezione sull'argomento matematica non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Curve trasverse sulla superficie di una sfera Curve non trasverse sulla superficie di una sfera In matematica, e più precisamente in topologia differenziale, la trasversalità è una proprietà opposta alla ta...