Fakultet (matematik)
|
Read other articles:

Artikel ini tidak memiliki bagian pembuka yang sesuai dengan standar Wikipedia. Mohon tulis paragraf pembuka yang informatif sehingga pembaca dapat memahami maksud dari Laura Bridgman. Contoh paragraf pembuka Laura Bridgman adalah .... (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Laura Dewey Bridgman (21 Desember 1829 – 24 Mei 1889) adalah seorang tunaganda buta-tuli berbahasa Inggris pertama di Amerika yang mempelajari cara berkomunikasi dengan mengeja ...

Mosque in Mersin, Turkey Laal Pasha MosqueReligionAffiliationIslamProvinceMersin ProvinceRegionMediterranean RegionRiteSunni IslamStatusActiveLocationLocationMersin, TurkeyArchitectureTypeMosqueCompleted1444 Mausoleum Interior Laal Pasha Mosque is a Medieval mosque in Mut in Mersin Province, Turkey. (Names such as Lal Pasha, Lael Pasha and Lala Agha are also used.) History Laal Pasha was a high-ranking bureaucrat in the Turkmen state of Karamanids in Anatolia. In his youth he was a servant of...

Poster Perang Dunia II dari Angkatan Bersenjata Amerika tentang Jepang yang diasosiasikan sebagai tikus (binatang yang merugikan) mendekati perangkap yang diberi tanda Angkatan Laut, Angkatan Darat, Sipil, sebagai latar belakang peta negara bagian AlaskaPropaganda (dalam bahasa Latin modern: propagare diartikan mengembangkan atau memekarkan)[1], diayah, atau daayah merupakan serangkaian pesan dengan tujuan agar dapat memengaruhi pendapat seseorang, tindakan masyarakat atau sekelompok ...

Khaplu ཁལུ་خپلوCountryPakistanProvinsiGilgit–BaltistanDistrikGhangchePemerintahan • NooraniSyed Muhammad ShahKetinggian8.400 ft (2.560 m)Populasi • Total83.200Zona waktuUTC+5 (PST) • Musim panas (DST)UTC+6 (GMT+6) Khaplu (Urdu:خپلو) adalah ibu kota administratif ditrik Ghangche Gilgit-Baltistan . Berjarak 103 km (64 mil) sebelah timur dari kota Skardu kota terbesar kedua di Baltistan . Khaplu berada di rute perdagangan ke Ladakh ...

American politician John F. Ryan37th Speaker of the Virginia House of DelegatesIn officeDecember 4, 1901 – January 10, 1906Preceded byEdward W. SaundersSucceeded byWilliam D. CardwellIn officeMarch 3, 1894 – December 6, 1899Preceded byRichard H. CardwellSucceeded byEdward W. SaundersMember of the Virginia House of Delegates from Loudoun CountyIn officeDecember 5, 1883 – January 10, 1906Preceded byGeorge E. PlasterSucceeded byFenton M. Love Personal details...

2018 single by Hebe TienStaySingle by Hebe TienLanguageMandarinReleased20 August 2018GenreMandopopLength4:11Composer(s)Yu Hsuan Lin (林祐萱)Lyricist(s)Hebe TienProducer(s)Sandee ChanHebe Tien singles chronology Miserable Warmth (2018) Stay (2018) Jasper Night (2018) Music videoStay on YouTube Stay (Chinese: 自己的房間; pinyin: 自己的房間; lit. 'A Room of One's Own') is a song recorded by Taiwanese singer Hebe Tien released on 20 August 2018 under HIM International...

Voce principale: Rovigo Calcio. Associazione Calcio Pro RovigoStagione 1946-1947Sport calcio Squadra Pro Rovigo Allenatore Cesare Zancanaro Presidente Bruno Granata Serie C6º nel girone H Nord. Maggiori presenzeCampionato: Menin (30) Miglior marcatoreCampionato: Cattozzo (9) 1945-1946 1947-1948 Si invita a seguire il modello di voce Questa pagina raccoglie le informazioni riguardanti l'Associazione Calcio Pro Rovigo nelle competizioni ufficiali della stagione 1946-1947. Stagione Nella ...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...
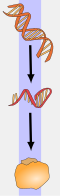
لمعانٍ أخرى، طالع ترجمة (توضيح). رسم بياني يوضح ترجمة ال mRNA وتكوين البروتينات بواسطة الريبوسوم في علم الوراثة، الترجمة هي المرحلة الثانية في عملية الاصطناع الحيوي للبروتين (و التي تشكل جزءا من عملية التعبير الجيني).[1][2][3] في هذه المرحلة يتم فك تشفير المعل�...

Lambang Peta lokasi Tauragė ialah sebuah kota industri di Lituania barat dan ibu kota Kabupaten Tauragė. Kota ini berpenduduk 28.504 jiwa (2005). Tauragė terletak di bantaran sungai Jūra dekat perbatasan Oblast Kaliningrad, Rusia dan tidak jauh dari Laut Baltik. Kota ini menerima hak kota pada tahun 1932. Lambangnya (tanduk emas dengan warna latar merah) dirancang pada tahun 1997. Kota ini terkenal akan sejumlah bangunannya, termasuk istana Radziwiłł yang bercorak neo-Gothik (sekarang k...

Public university in Joplin, Missouri, U.S. Missouri Southern State UniversityFormer namesJoplin Junior College (1937–1977)Missouri Southern State College (1977–2003)Missouri Southern State University–Joplin (2003–2005)TypePublic universityEstablished1937 (1937)PresidentDean Van GalenProvostLisa TomsStudents4,087 (Fall 2023) [1]LocationJoplin, Missouri, U.S.37°05′45″N 94°27′44″W / 37.09595°N 94.46220°W / 37.09595; -94.46220CampusUrban, ...

Former Pakistani airline This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bhoja Air – news · newspapers · books · scholar · JSTOR (August 2013) (Learn how and when to remove this message) Bhoja Air IATA ICAO Callsign B4 BHO BHOJA Founded1993Commenced operations7 November 19936 March 2012 (relaunch)Ceased oper...

Russian politician (born 1965) Anatoly SeryshevАнатолий Серышев6th Plenipotentiary Representative in the Siberian Federal DistrictIncumbentAssumed office 12 October 2021Preceded bySergey MenyayloAssistant to the President of Russia [ru]In office13 June 2018 – 12 October 2021Deputy Director of the Federal Customs ServiceIn office2016–2018 Personal detailsBornAnatoly Anatolyevich Seryshev (1965-07-19) 19 July 1965 (age 58)Koblyakovo [ru...

Домовый воробей Самец домового воробья[1] Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:Амни�...

2014 film directed by David Dhawan Main Tera HeroTheatrical release posterDirected byDavid DhawanWritten byScreenplay:Tushar HiranandaniDialogues:Milap ZaveriStory byTushar HiranandaniBased onKandireegaby Santosh Srinivas and Anil RavipudiProduced byShobha KapoorEkta KapoorStarringVarun DhawanIleana D'CruzNargis Fakhri Narrated bySalman KhanCinematographySanjay F. GuptaMusic bySongs:Sajid–WajidScore:Sandeep ShirodkarProductioncompanyBalaji Motion PicturesRelease date April 4, 2014...

1981 single by Electric Light OrchestraTicket to the MoonSingle by Electric Light Orchestrafrom the album Time A-sideHere Is the NewsReleased11 December 1981 (UK)Recorded1981StudioMusicland, Munich, GermanyGenreArt rockLength4:07LabelJetSongwriter(s)Jeff LynneProducer(s)Jeff LynneElectric Light Orchestra singles chronology Twilight (1981) Ticket to the Moon (1981) Rain Is Falling (1982) Time track listing13 tracks Side one Prologue Twilight Yours Truly, 2095 Ticket to the Moon The Way Life's ...

Questa voce sull'argomento calciatori tedeschi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Robin BormuthNazionalità Germania Altezza190 cm Peso87 kg Calcio RuoloDifensore Squadra Karlsruhe CarrieraGiovanili -2013 Darmstadt2013-2014 Fortuna Düsseldorf Squadre di club1 2014-2015 F. Düsseldorf II60 (2)2015-2020 Fortuna Düsseldorf56 (3)2020-2022 Karlsruhe35 (4)202...

Central IntelligencePoster rilis teatrikalSutradaraRawson Marshall ThurberProduser Michael Fottrell Peter Principato Scott Stuber Paul Young Skenario Ike Barinholtz David Stassen Rawson Marshall Thurber Cerita Ike Barinholtz David Stassen Pemeran Dwayne Johnson Kevin Hart Amy Ryan Aaron Paul Penata musik Theodore Shapiro Ludwig Göransson SinematograferBarry PetersonPenyuntingMichael L. SalePerusahaanproduksi New Line Cinema Bluegrass Films Principato-Young Entertainment RatPac-Dune Ent...

Month of 1945 1945 January February March April May June July August September October November December << July 1945 >> Su Mo Tu We Th Fr Sa 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 July 16, 1945: Trinity (nuclear test) The following events occurred in July 1945: July 1, 1945 (Sunday) The Battle of Balikpapan began when Australian and Dutch troops made an amphibious landing a few miles north of Balikpapan, Borneo. The Inn...

Socket 4 ソケット形式 ZIFチップ形状 PPGA接点数(ピン数) 273ピンFSBプロトコル ?電圧範囲 5 V採用プロセッサ Intel Pentiumこの記事はCPUソケットシリーズの一部です Socket 4 は、初期の Pentium プロセッサ向けに設計されたCPUソケットであり、1993年に発表された。Socket 4 は、5 V 動作の Pentium 専用であった。Socket 4 のあと、インテルは 3.3 V に対応した Socket 5 に切り替えた。Socket 4 ...














