Фактор аеродинамичког оптерећења
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:
Maicon Informasi pribadiNama lengkap Maicon Douglas SisenandoTanggal lahir 26 Juli 1981 (umur 42)Tempat lahir Novo Hamburgo, Rio Grande do Sul, BrasilTinggi 184 m (603 ft 8 in)Posisi bermain Pemain belakangInformasi klubKlub saat ini AS RomaNomor 13Karier junior Grêmio Criciúma CruzeiroKarier senior*Tahun Tim Tampil (Gol)2001–2004 Cruzeiro 56 (1)2004–2006 Monaco 58 (5)2006–2012 Inter Milan 177 (16)2012–2013 Manchester City 9 (0)2013– AS Roma 16 (2)Tim nasional...

Nuevo Solnuevo sol peruano (Spanyol) 1 nuevo sol (Tampak Muka)1 nuevo sol (Tampak Belakang) ISO 4217KodePENDenominasiSubsatuan 1/100céntimoBentuk jamaknuevos soles céntimocéntimosSimbolS/.Uang kertas Sering digunakan10, 20, 50 & 100 nuevos soles Jarang digunakan200 nuevos solesUang koin Sering digunakan10, 20 & 50 céntimos, 1, 2 & 5 nuevos soles Jarang digunakan5 céntimosDemografiPengguna PeruEmisiBank sentralCentral Reserve Bank of Pe...

NGM-81 Jenis Senapan serbu Negara asal Hungaria Sejarah pemakaian Digunakan oleh Hungaria Spesifikasi Peluru 5,45 x 39 mm5,56 x 45 mm Mekanisme Operasi gas Amunisi Magazen box 30 butir NGM atau NGM-81 adalah senapan serbu buatan Hungaria hasil adposi dari AK-74 dan menggunakan peluru 5,45 x 39 mm. Varian ekspor dari senapan ini menggunakan peluru 5,56 x 45 mm.[1] Selain popor tetap senapan ini dibuat juga dengan popor besi lipat dengan nama NGV.[2] Catatan kak...

Synthetic cannabinoid, designer drug ADB-5'Br-PINACALegal statusLegal status DE: NpSG (Industrial and scientific use only) UK: Class B Identifiers IUPAC name N-(1-Amino-3,3-dimethyl-1-oxo-2-butanyl)-1-pentyl-1H-5-bromoindazole-3-carboxamide PubChem CID168310461ChemSpider115285280Chemical and physical dataFormulaC19H27BrN4O2Molar mass423.355 g·mol−13D model (JSmol)Interactive image SMILES NC(=O)[C@@H](NC(=O)c1nn(CCCCC)c2ccc(Br)cc21)C(C)(C)C InChI InChI=1S/C19H27BrN4O2/c1-...

Politik Hijau merupakan istilah yang berasal dari bahasa Jerman Grün, disatukan oleh die Grünen, sebuah partai Hijau yang terbentuk di akhir 1970-an. Kadang-kadang istilah ekologi politik digunakan di Eropa dan di lingkaran akademis, tetapi yang belakangan telah mulai mewakili ranah kajian lintas-disiplin, termasuk kimia dan teknik kimia. Politik hijau yang biasa disebut sebagai Green Party adalah pemahaman bahwa titik berat kehidupan bukan pada ekonomi melainkan pada alam (Ekosentris), lan...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

Halaman ini berisi artikel tentang Gol & Gincu. Untuk serial televisi, lihat Gol & Gincu The Series. Gol & GincuSutradaraBernard ChaulyProduserLina TanPemeranNur FazuraSazzy FalakAshraf SinclairMelissa MaureenPierre AndrePenata musikGreg HendersonPerusahaanproduksiGolden Screen Cinemas Red CommunicationsTanggal rilis11 Agustus 2005Durasi95 menitNegaraMalaysiaBahasaBahasa Melayu Gol Dan Gincu adalah sebuah film romansa yang diadaptasi dari sebuah cerita karya Lina Tan dan Raf...

Объект всемирного наследия ЮНЕСКО[* 1]Shahr-i Sokhta[* 2] Страна Иран Тип Культурный Критерии ii, iii, iv Ссылка 1456 Регион[* 3] Объекты ЮНЕСКО в Азии Включение 2014 год (38-я сессия) ↑ Название в официальном рус. списке ↑ Название в официальном англ. списке ↑ Регион по класси...

French Swimming FederationFédération Française de NatationSportswimming, diving, synchronized swimming, water polo, open water swimmingAbbreviation(FFN)Founded1919AffiliationInternational Swimming Federation (FINA)European Swimming League(LEN)LocationParis, FrancePresidentGilles Sezionale, since 2017Official websitewww.ffnatation.fr The French Swimming Federation (French: Fédération française de natation, FFN) is the French water sports association. Founded in February 1919, it grouped ...

Liga 3 2017 PapuaMusim2017JuaraPersido Dogiyai[1]← 2014 2018 → Liga 3 2017 Papua (juga dikenal sebagai Piala Gubernur Papua 2017) adalah edisi ketiga dari Liga 3 di wilayah Provinsi Papua sebagai babak kualifikasi untuk putaran nasional dari Liga 3 2017. Persintan Intan Jaya adalah juara bertahan. Kompetisi dijadwalkan untuk dibuka pada tanggal 24 Mei 2017.[2] Tim Ada 19 tim yang akan berpartisipasi di liga pada musim ini. Grup A Persidafon Dafonsoro Emsyk FC Persiyali Yal...

Halaman ini berisi artikel tentang reorganisasi struktur bisnis. Untuk kegunaan lain, lihat Restrukturisasi (disambiguasi). Artikel ini memiliki beberapa masalah. Tolong bantu memperbaikinya atau diskusikan masalah-masalah ini di halaman pembicaraannya. (Pelajari bagaimana dan kapan saat yang tepat untuk menghapus templat pesan ini) Artikel ini tidak memiliki bagian pembuka yang sesuai dengan standar Wikipedia. Mohon tulis paragraf pembuka yang informatif sehingga pembaca dapat memahami maksu...

Association football club in Perth, Scotland Football clubLethamFull nameLetham Football ClubNickname(s)TangerinesFounded1960GroundSeven AcresPerthCapacity300LeagueSJFA Midlands League2022–23SJFA Midlands League, 9th of 19 Home colours Away colours Letham are a Scottish football club from the Letham area in the northwest of Perth. They are members of the East Region of the Scottish Junior Football Association and currently play in the Midlands Football League.[1] History Letham were...
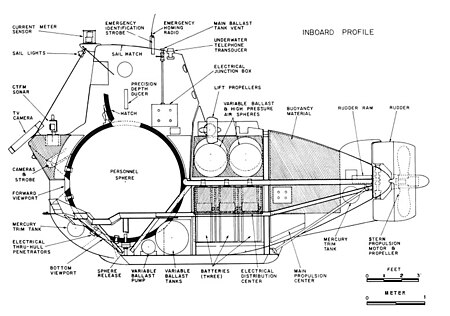
Crewed deep-ocean research submersible ALVIN redirects here. For other uses, see Alvin. Alvin in 1978, a year after first exploring hydrothermal vents. The rack hanging at the bow holds sample containers. History United States NameAlvin NamesakeAllyn Vine OperatorWoods Hole Oceanographic Institution BuilderGeneral Mills' Electronics Group[1] AcquiredMay 26, 1964 In serviceJune 5, 1964 Statusin active service, as of 2023[ref] General characteristics [2] TypeDeep-submerg...

Alternative term for women, designed to avoid perceived sexism It has been suggested that this article be merged into Womyn. (Discuss) Proposed since May 2024. The term womxn is an alternative spelling of the English word woman. Womxn, along with the term womyn, has been found in writing since the 1970s to avoid perceived sexism in the standard spelling, which contains the word man.[1] The term womxn has been adopted by various organizations, including student university groups in the...

Finnish artistic gymnast Veikko HuhtanenPersonal informationCountry represented FinlandBorn(1919-06-05)5 June 1919Viipuri, FinlandDied29 January 1976(1976-01-29) (aged 56)DisciplineMen's artistic gymnastics Medal record Representing Finland Olympic Games 1948 London All-around 1948 London Pommel horse 1948 London Team all-around 1948 London Parallel bars 1948 London Horizontal bar World Championships 1950 Basel Horizontal bar 1950 Basel Team all-around Veikko Aarne A...

Play written by George Bernard Shaw For other uses, see Major Barbara (disambiguation). Major BarbaraThe Court Theatre 1904–1907Written byGeorge Bernard ShawDate premieredNovember 28, 1905[1]Place premieredCourt TheatreOriginal languageEnglishGenreDramaSettingLondon Major Barbara is a three-act English play by George Bernard Shaw, written and premiered in 1905 and first published in 1907. The story concerns an idealistic young woman, Barbara Undershaft, who is engaged in helping the...

بلانش الفرنسية (بالفرنسية: Blanche de France) معلومات شخصية الميلاد سنة 1253 [1] يافا الوفاة سنة 1320 (66–67 سنة) باريس مواطنة فرنسا الزوج فرناندو دي لا سيردا (1269–) الأولاد ألفونسو دي لا سيردافرناندو دي لا سيردا، لورد لارا الأب لويس التاسع الأم مار...

Mission school in IndiaSt Aloysius' Anglo-Indian High SchoolLocationOne Town, Visakhapatnam, Andhra PradeshIndiaCoordinates17°41′34″N 83°17′36″E / 17.69278°N 83.29333°E / 17.69278; 83.29333InformationTypeMission SchoolReligious affiliation(s)Roman CatholicEstablished1847; 177 years ago (1847)FounderBritish Indian ArmyGradesLKG - 10AffiliationICSEWebsiteOfficial Website St. Aloysius H. School in 1920. St Aloysius' Anglo-Indian High School ...

Le Triomphe de GalatéeArtiste RaphaëlDate 1513Commanditaire Agostino ChigiType Haute RenaissanceTechnique FresqueDimensions (H × L) 295 × 224 cmMouvement Haute RenaissanceLocalisation Villa Farnesina, Rome (Italie)modifier - modifier le code - modifier Wikidata Le Triomphe de Galatée est une peinture de Raphaël, une fresque (295 × 224 cm), réalisée en 1513 pour la Villa Farnesina, à Rome. Histoire La fresque est une partie de la commande q...

Serbian singer and songwriter Sanja VučićСања ВучићVučić in 2016Background informationBorn (1993-08-08) 8 August 1993 (age 31)Kruševac, Serbia, FR YugoslaviaGenresR&Bpopelectronicskadubpost-rockjazzOccupation(s)SingersongwriterInstrumentVocalsLabelsLil WolfFormerly ofZAAHurricaneMusical artist Sanja Vučić (Serbian Cyrillic: Сања Вучић, pronounced [sâɲa vûtʃitɕ]; born 8 August 1993) is a Serbian singer and songwriter. Initially the lead vocalist o...











































![{\displaystyle \ a=7\cdot 9,81\left[{\frac {m}{s^{2}}}\right]\Rightarrow \ a=88,29\left[{\frac {m}{s^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9526f45b39db9a25ad6b7ea8ca6b47aad50b2ca9)



