![]() –ö–ĺ—Ö–ĺ–≤–į –Ņ–į—Ö—É—ô–į –ł–ľ–į –Ī–Ķ—Ā–ļ–ĺ–Ĺ–į—á–Ĺ–ĺ –Ņ–ĺ–Ĺ–į–≤—ô–į—ö–Ķ —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ĺ—Ā—ā–ł –ļ–į–ī–į —Ā–Ķ —É–≤–Ķ—õ–į–≤–į
–ö–ĺ—Ö–ĺ–≤–į –Ņ–į—Ö—É—ô–į –ł–ľ–į –Ī–Ķ—Ā–ļ–ĺ–Ĺ–į—á–Ĺ–ĺ –Ņ–ĺ–Ĺ–į–≤—ô–į—ö–Ķ —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ĺ—Ā—ā–ł –ļ–į–ī–į —Ā–Ķ —É–≤–Ķ—õ–į–≤–į
 –°—ā–į–Ĺ–ī–į—Ä–ī–Ĺ–į (—ā—Ä–ł–≤–ł—ė–į–Ľ–Ĺ–į) —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ĺ—Ā—ā[1]
–°—ā–į–Ĺ–ī–į—Ä–ī–Ĺ–į (—ā—Ä–ł–≤–ł—ė–į–Ľ–Ĺ–į) —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ĺ—Ā—ā[1]
–£ –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł, —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–į–Ĺ –ĺ–Ī—ė–Ķ–ļ–į—ā —ė–Ķ —ā–į—á–Ĺ–ĺ –ł–Ľ–ł –Ņ—Ä–ł–Ī–Ľ–ł–∂–Ĺ–ĺ —Ā–Ľ–ł—á–į–Ĺ –ī–Ķ–ĺ —Ā–Ķ–Ī–Ķ (—ā—ė —Ü–Ķ–ĺ –ł–ľ–į –ł—Ā—ā–ł –ĺ–Ī–Ľ–ł–ļ –ļ–į–ĺ —ė–Ķ–ī–į–Ĺ –ł–Ľ–ł –≤–ł—ą–Ķ –ī–Ķ–Ľ–ĺ–≤–į). –ú–Ĺ–ĺ–≥–ł –ĺ–Ī—ė–Ķ–ļ—ā–ł —É —Ā—ā–≤–į—Ä–Ĺ–ĺ–ľ —Ā–≤–Ķ—ā—É, –ļ–į–ĺ —ą—ā–ĺ —Ā—É –ĺ–Ī–į–Ľ–Ķ, —Ā—ā–į—ā–ł—Ā—ā–ł—á–ļ–ł —Ā—É —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ł: –ī–Ķ–Ľ–ĺ–≤–ł —ö–ł—Ö –Ņ–ĺ–ļ–į–∑—É—ė—É –ł—Ā—ā–Ķ —Ā—ā–į—ā–ł—Ā—ā–ł—á–ļ–Ķ –ĺ—Ā–ĺ–Ī–ł–Ĺ–Ķ –Ĺ–į –ľ–Ĺ–ĺ–≥–ł–ľ —Ā–ļ–į–Ľ–į–ľ–į.[2] –°–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ĺ—Ā—ā —ė–Ķ —ā–ł–Ņ–ł—á–Ĺ–ĺ –≤–Ľ–į—Ā–Ĺ–ł—ą—ā–≤–ĺ —Ą—Ä–į–ļ—ā–į–Ľ–į. –°–ļ–į–Ľ–į –ł–Ĺ–≤–į—Ä–ł—ė–į–Ĺ—ā–Ĺ–ĺ—Ā—ā–ł —ė–Ķ —ā–į—á–į–Ĺ –ĺ–Ī–Ľ–ł–ļ –≥–ī–Ķ –∑–į —Ā–≤–į–ļ–ĺ —É–≤–Ķ—õ–į—ö–Ķ –Ņ–ĺ—Ā—ā–ĺ—ė–ł –ľ–į—ö–ł –ī–Ķ–ĺ –ĺ–Ī—ė–Ķ–ļ—ā–į –ļ–ĺ—ė–ł —ė–Ķ —Ā–Ľ–ł—á–į–Ĺ —Ü–Ķ–Ľ–ł–Ĺ–ł. –Ě–į –Ņ—Ä–ł–ľ–Ķ—Ä, —Ā—ā—Ä–į–Ĺ–į –ö–ĺ—Ö–ĺ–≤–Ķ –Ņ–į—Ö—É—ô–Ķ —ė–Ķ –ł —Ā–ł–ľ–Ķ—ā—Ä–ł—á–Ĺ–į –ł —Ā–ļ–į–Ľ–Ĺ–ĺ-–ł–Ĺ–≤–į—Ä–ł—ė–į–Ĺ—ā–Ĺ–į; –ľ–ĺ–∂–Ķ —Ā–Ķ –ļ–ĺ–Ĺ—ā–ł–Ĺ—É–ł—Ä–į–Ĺ–ĺ —É–≤–Ķ—õ–į—ā–ł 3 –Ņ—É—ā–į –Ī–Ķ–∑ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–į –ĺ–Ī–Ľ–ł–ļ–į. –Ě–Ķ-—ā—Ä–ł–≤–ł—ė–į–Ľ–Ĺ–Ķ —Ā–Ľ–ł—á–Ĺ–ĺ—Ā—ā–ł —É —Ą—Ä–į–ļ—ā–į–Ľ–ł–ľ–į —Ā–Ķ —Ä–į–∑–Ľ–ł–ļ—É—ė—É –Ņ–ĺ —Ā–≤–ĺ—ė–ĺ—ė —Ā—ā—Ä—É–ļ—ā—É—Ä–ł, –ł–Ľ–ł —Ą–ł–Ĺ–ł–ľ –ī–Ķ—ā–į—ô–ł–ľ–į –Ĺ–į –Ņ—Ä–ĺ–ł–∑–≤–ĺ—ô–Ĺ–ĺ –ľ–į–Ľ–ł–ľ —Ā–ļ–į–Ľ–į–ľ–į. –ö–į–ĺ –Ņ—Ä–ĺ—ā–ł–≤ –Ņ—Ä–ł–ľ–Ķ—Ä, –ī–ĺ–ļ –Ī–ł–Ľ–ĺ –ļ–ĺ—ė–ł –ī–Ķ–ĺ –Ņ—Ä–į–≤–Ķ –Ľ–ł–Ĺ–ł—ė–Ķ –ľ–ĺ–∂–Ķ –Ľ–ł—á–ł—ā–ł –Ĺ–į —Ü–Ķ–Ľ–ł–Ĺ—É, –ī–į—ô–ł –ī–Ķ—ā–į—ô –Ĺ–ł—ė–Ķ –ĺ—ā–ļ—Ä–ł–≤–Ķ–Ĺ.
–Ē–Ķ—Ą–ł–Ĺ–ł—Ü–ł—ė–į
–ö–ĺ–ľ–Ņ–į–ļ—ā–Ĺ–ł —ā–ĺ–Ņ–ĺ–Ľ–ĺ—ą–ļ–ł –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä –• —ė–Ķ —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–į–Ĺ –į–ļ–ĺ –Ņ–ĺ—Ā—ā–ĺ—ė–ł –ļ–ĺ–Ĺ–į—á–Ĺ–ł —Ā–ļ—É–Ņ –° –ļ–ĺ—ė–ł –ł–Ĺ–ī–Ķ–ļ—Ā–ł—Ä–į –Ĺ–Ķ-—Ā—É—Ä—ė–Ķ–ļ—ā–ł–≤–Ĺ–Ķ —Ö–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ–Ķ  –∑–į –ļ–ĺ—ė–Ķ
–∑–į –ļ–ĺ—ė–Ķ

–ź–ļ–ĺ —ė–Ķ  , —ā–į–ī–į X –∑–ĺ–≤–Ķ–ľ–ĺ —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ł–ľ –į–ļ–ĺ —ė–Ķ –ĺ–Ĺ —ė–Ķ–ī–ł–Ĺ–ł –Ĺ–Ķ-–Ņ—Ä–į–∑–Ĺ–ł –Ņ–ĺ–ī—Ā–ļ—É–Ņ –ĺ–ī Y —ā–į–ļ–į–≤ –ī–į —ė–Ķ –≥–ĺ—Ä—ö–į —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–į –∑–į–ī–ĺ–≤–ĺ—ô–Ķ–Ĺ–į –∑–į
, —ā–į–ī–į X –∑–ĺ–≤–Ķ–ľ–ĺ —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ł–ľ –į–ļ–ĺ —ė–Ķ –ĺ–Ĺ —ė–Ķ–ī–ł–Ĺ–ł –Ĺ–Ķ-–Ņ—Ä–į–∑–Ĺ–ł –Ņ–ĺ–ī—Ā–ļ—É–Ņ –ĺ–ī Y —ā–į–ļ–į–≤ –ī–į —ė–Ķ –≥–ĺ—Ä—ö–į —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–į –∑–į–ī–ĺ–≤–ĺ—ô–Ķ–Ĺ–į –∑–į  . –ú–ł –∑–ĺ–≤–Ķ–ľ–ĺ
. –ú–ł –∑–ĺ–≤–Ķ–ľ–ĺ

—Ā–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ĺ–ľ —Ā—ā—Ä—É–ļ—ā—É—Ä–ĺ–ľ. –•–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ–ł –ľ–ĺ–≥—É –Ī–ł—ā–ł –ł—ā–Ķ—Ä–ł—Ä–į–Ĺ–ł —ą—ā–ĺ —Ä–Ķ–∑—É–Ľ—ā–ł—Ä–į —Ā–ł—Ā—ā–Ķ–ľ–ĺ–ľ –ł—ā–Ķ—Ä–ł—Ä–į–Ĺ–Ķ —Ą—É–Ĺ–ļ—Ü–ł—ė–Ķ. –ö–ĺ–ľ–Ņ–ĺ–∑–ł—Ü–ł—ė–į —Ą—É–Ĺ–ļ—Ü–ł—ė–į —Ā—ā–≤–į—Ä–į –į–Ľ–≥–Ķ–Ī–į—Ä—Ā–ļ—É —Ā—ā—Ä—É–ļ—ā—É—Ä—É –Ņ–ĺ–∑–Ĺ–į—ā—É –ļ–į–ĺ –ľ–ĺ–Ĺ–ĺ–ł–ī. –ö–į–ī —Ā–ļ—É–Ņ S –ł–ľ–į —Ā–≤–Ķ–≥–į –ī–≤–į –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į –ľ–ĺ–Ĺ–ĺ–ł–ī —ė–Ķ –Ņ–ĺ–∑–Ĺ–į—ā –ļ–į–ĺ –ī–ł–į–ī–ł—á–ļ–ł –ľ–ĺ–Ĺ–ĺ–ł–ī. –Ē–ł–į–ī–ł—á–ļ–ł –ľ–ĺ–Ĺ–ĺ–ł–ī –ľ–ĺ–∂–Ķ –Ī–ł—ā–ł –≤–ł–∑—É–Ķ–Ľ–Ĺ–ĺ –Ņ—Ä–ł–ļ–į–∑–į–Ĺ –ļ–į–ĺ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–į—á–Ĺ–ĺ –Ī–ł–Ĺ–į—Ä–Ĺ–ĺ —Ā—ā–į–Ī–Ľ–ĺ- –≥–Ķ–Ĺ–Ķ—Ä–į–Ľ–Ĺ–ł—ė–Ķ, ako —Ā–ļ—É–Ņ S –ł–ľ–į p –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ–į—ā–į, –ľ–ĺ–Ņ–Ĺ–ĺ–ł–ī –ľ–ĺ–∂–Ķ –Ī–ł—ā–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—ô–Ķ–Ĺ –Ņ-–į–ī–ł—á–ļ–ł–ľ —Ā—ā–į–Ī–Ľ–ĺ–ľ.
–ź—É—ā–ĺ–ľ–ĺ—Ä—Ą–ł–∑–į–ľ –ī–ł–į–ī–ł—á–ļ–ĺ–≥ –ľ–ĺ–Ĺ–ĺ–ł–ī–į —ė–Ķ –ľ–ĺ–ī—É–Ľ–į—Ä–Ĺ–į –≥—Ä—É–Ņ–į, –į—É—ā–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ–ł –ľ–ĺ–≥—É –Ī–ł—ā–ł –Ĺ–į—Ā–Ľ–ł–ļ–į–Ĺ–ł –ļ–į–ĺ —Ö–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–ł—á–ļ–Ķ —Ä–ĺ—ā–į—Ü–ł—ė–Ķ –Ī–ł–Ĺ–į—Ä–Ĺ–ĺ–≥ —Ā—ā–į–Ī–Ľ–į.
–ě–Ņ—ą—ā–ł—ė–ł –Ņ–ĺ—ė–į–ľ –ĺ–ī —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ĺ—Ā—ā–ł —ė–Ķ —Ā–į–ľ–ĺ-–į—Ą–ł–Ĺ–ł—ā–Ķ—ā.
–ü—Ä–ł–ľ–Ķ—Ä–ł
 –°–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ĺ—Ā—ā —É –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā–ĺ–≤–ĺ–ľ —Ā–ļ—É–Ņ—É –Ņ–ĺ–ļ–į–∑–į–Ĺ–ĺ –∑—É–ľ–ł—Ä–į—ö–Ķ–ľ —É –§–į—ė–≥–Ķ–ľ–Ī–į—É–ľ–ĺ–≤–Ķ —ā–į—á–ļ–Ķ —É(‚ąí1.401155189..., 0)
–°–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ĺ—Ā—ā —É –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā–ĺ–≤–ĺ–ľ —Ā–ļ—É–Ņ—É –Ņ–ĺ–ļ–į–∑–į–Ĺ–ĺ –∑—É–ľ–ł—Ä–į—ö–Ķ–ľ —É –§–į—ė–≥–Ķ–ľ–Ī–į—É–ľ–ĺ–≤–Ķ —ā–į—á–ļ–Ķ —É(‚ąí1.401155189..., 0)
 –°–Ľ–ł–ļ–į –Ņ–į–Ņ—Ä–į—ā–ł –ļ–ĺ—ė–į –Ņ–ĺ–ļ–į–∑—É—ė–Ķ —Ā—Ä–ĺ–ī–Ĺ—É —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ĺ—Ā—ā
–°–Ľ–ł–ļ–į –Ņ–į–Ņ—Ä–į—ā–ł –ļ–ĺ—ė–į –Ņ–ĺ–ļ–į–∑—É—ė–Ķ —Ā—Ä–ĺ–ī–Ĺ—É —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ĺ—Ā—ā
–ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā–ĺ–≤ —Ā–ļ—É–Ņ —ė–Ķ —ā–į–ļ–ĺ—í–Ķ —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–į–Ĺ –ĺ–ļ–ĺ –ú–ł—Ā–ł—É—Ä–Ķ–≤–ł—Ü —ā–į—á–į–ļ–į.
–°–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ĺ—Ā—ā –ł–ľ–į –∑–Ĺ–į—á–į—ė–Ĺ–Ķ –Ņ–ĺ—Ā–Ľ–Ķ–ī–ł—Ü–Ķ –∑–į –Ņ—Ä–ĺ—ė–Ķ–ļ—ā–ĺ–≤–į—ö–Ķ —Ä–į—á—É–Ĺ–į—Ä—Ā–ļ–ł—Ö –ľ—Ä–Ķ–∂–į, —ā–ł–Ņ–ł—á–Ĺ–Ķ —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–Ķ –ĺ—Ā–ĺ–Ī–ł–Ĺ–Ķ –ł–ľ–į –ľ—Ä–Ķ–∂–Ĺ–ł —Ā–į–ĺ–Ī—Ä–į—õ–į—ė. –Ě–į –Ņ—Ä–ł–ľ–Ķ—Ä, —É –ł–Ĺ–∂–Ķ—ö–Ķ—Ä—Ā—ā–≤—É —Ā–į–ĺ–Ī—Ä–į—õ–į—ė–į, —ā–Ķ—Ö–Ĺ–ĺ–Ľ–ĺ–≥–ł—ė–į –Ņ–į–ļ–Ķ—ā–Ĺ–ĺ–≥ –Ņ—Ä–Ķ–Ĺ–ĺ—Ā–į –Ņ–ĺ–ī–į—ā–į–ļ–į –ĺ–Ī—Ä–į–∑–į—Ü–į –ł–∑–≥–Ľ–Ķ–ī–į —Ā—ā–į—ā–ł—Ā—ā–ł—á–ļ–ł —Ā–Ķ–Ī–ł—Ā–Ľ–ł—á–Ĺ–ĺ.[3]–ě–≤–į –Ĺ–Ķ–ļ—Ä–Ķ—ā–Ĺ–ł–Ĺ–į –∑–Ĺ–į—á–ł –ī–į —ė–Ķ–ī–Ĺ–ĺ—Ā—ā–į–≤–Ĺ–ł –ľ–ĺ–ī–Ķ–Ľ–ł –ļ–ĺ—ė–ł –ļ–ĺ—Ä–ł—Ā—ā–Ķ –ī–ł—Ā—ā—Ä–ł–Ī—É—Ü–ł—ė—É –ü–ĺ–ł—Ā–ĺ–Ĺ–ĺ–≤—É —Ā—É –Ĺ–Ķ—ā–į—á–Ĺ–ł, –ł –ľ—Ä–Ķ–∂–Ķ –Ņ—Ä–ĺ—ė–Ķ–ļ—ā–ĺ–≤–į–Ĺ–Ķ –Ī–Ķ–∑ —É–∑–ł–ľ–į—ö–į —Ā–Ķ–Ī–ł—Ā–Ľ–ł—á–Ĺ–ĺ—Ā—ā–ł —É –ĺ–Ī–∑–ł—Ä –≤–Ķ—Ä–ĺ–≤–į—ā–Ĺ–ĺ –ī–į —Ą—É–Ĺ–ļ—Ü–ł–ĺ–Ĺ–ł—ą—É –Ĺ–į –Ĺ–Ķ–ĺ—á–Ķ–ļ–ł–≤–į–Ĺ–Ķ –Ĺ–į—á–ł–Ĺ–Ķ.
–°–Ľ–ł—á–Ĺ–ĺ —ā–ĺ–ľ–Ķ, –Ī–Ķ—Ä–∑–Ķ —Ā—É –ĺ–Ņ–ł—Ā–į–Ĺ–Ķ –ļ–į–ĺ –Ņ—Ä–ł–ļ–į–∑ —Ā–į–ľ–ĺ–į—Ą–ł–Ĺ–ł—ā–Ķ—ā–į, –ĺ–ī–Ĺ–ĺ—Ā–Ĺ–ĺ –ĺ–Ĺ–Ķ —Ā–Ķ –Ņ–ĺ—ė–į–≤—ô—É—ė—É —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–Ķ –ļ–į–ī–į —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–ł—Ā–į—ö–Ķ –Ņ—Ä–Ķ–ļ–ĺ –ĺ–ī–≥–ĺ–≤–į—Ä–į—ė—É—õ–Ķ —Ā—Ä–ĺ–ī–Ĺ–Ķ —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł—ė–Ķ –∑–į –Ĺ–ł–≤–ĺ –ī–Ķ—ā–į—ô–į –Ī—É–ī–Ķ –Ņ—Ä–ł–ļ–į–∑–į–Ĺ–ĺ.[4] –ē–Ĺ–ī—Ä—É –õ–ĺ –ĺ–Ņ–ł—Ā—É—ė–Ķ –Ī–Ķ—Ä–∑–Ķ –Ē–Ĺ–Ķ–≤–Ĺ–ł–ļ –Ņ–ĺ–≤—Ä–į—ā–ļ–į —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ĺ—Ā—ā–ł —É –Ķ–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—ė—É.[5]
–ö–ĺ–Ĺ–į—á–Ĺ–į –Ņ–ĺ–ī–Ķ–ĺ–Ĺ–į –Ņ—Ä–į–≤–ł–Ľ–į —Ā—É –ľ–ĺ—õ–Ĺ–į —ā–Ķ—Ö–Ĺ–ł–ļ–į –∑–į –ł–∑–≥—Ä–į–ī—ö—É —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ł—Ö —Ā–ļ—É–Ņ–ĺ–≤–į, —É–ļ—ô—É—á—É—ė—É—õ–ł –ö–į–Ĺ—ā–ĺ—Ä —Ā–ļ—É–Ņ –ł –°—ė–Ķ—Ä–Ņ–ł—ö—Ā–ļ–ł —ā—Ä–ĺ—É–≥–į–ĺ.
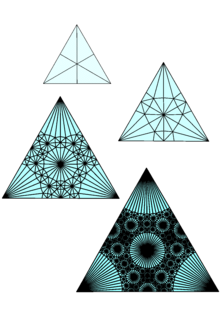 –Ę—Ä–ĺ—É–≥–į–ĺ –Ņ–ĺ–ī–Ķ—ô–Ķ–Ĺ —É –≤–ł—ą–Ķ –Ĺ–į–≤—Ä–į—ā–į –ļ–ĺ—Ä–ł—Ā—ā–ł –Ī–į—Ä–ł—Ü–Ķ–Ĺ—ā—Ä–ł—á–Ĺ—É –Ņ–ĺ–ī–Ķ–Ľ—É. –ö–ĺ–ľ–Ņ–Ľ–Ķ–ľ–Ķ–Ĺ—ā –≤–Ķ–Ľ–ł–ļ–ł—Ö –ļ—Ä—É–≥–ĺ–≤–į –Ņ–ĺ—Ā—ā–į—ė–Ķ –°—ė–Ķ—Ä–Ņ–ł—ö—Ā–ļ–ł —ā–Ķ–Ņ–ł—Ö
–Ę—Ä–ĺ—É–≥–į–ĺ –Ņ–ĺ–ī–Ķ—ô–Ķ–Ĺ —É –≤–ł—ą–Ķ –Ĺ–į–≤—Ä–į—ā–į –ļ–ĺ—Ä–ł—Ā—ā–ł –Ī–į—Ä–ł—Ü–Ķ–Ĺ—ā—Ä–ł—á–Ĺ—É –Ņ–ĺ–ī–Ķ–Ľ—É. –ö–ĺ–ľ–Ņ–Ľ–Ķ–ľ–Ķ–Ĺ—ā –≤–Ķ–Ľ–ł–ļ–ł—Ö –ļ—Ä—É–≥–ĺ–≤–į –Ņ–ĺ—Ā—ā–į—ė–Ķ –°—ė–Ķ—Ä–Ņ–ł—ö—Ā–ļ–ł —ā–Ķ–Ņ–ł—Ö
–£ –Ņ—Ä–ł—Ä–ĺ–ī–ł
 –Ē–Ķ—ā–į—ô–į–Ĺ —Ā–Ĺ–ł–ľ–į–ļ –†–ł–ľ—Ā–ļ–ĺ–≥ –Ī—Ä–ĺ–ļ–ĺ–Ľ–ł—ė–į
–Ē–Ķ—ā–į—ô–į–Ĺ —Ā–Ĺ–ł–ľ–į–ļ –†–ł–ľ—Ā–ļ–ĺ–≥ –Ī—Ä–ĺ–ļ–ĺ–Ľ–ł—ė–į
–°–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ĺ—Ā—ā –ľ–ĺ–∂–Ķ —Ā–Ķ –Ĺ–į—õ–ł —É –Ņ—Ä–ł—Ä–ĺ–ī–ł, —ā–į–ļ–ĺ—í–Ķ. –°–į –ī–Ķ—Ā–Ĺ–Ķ —Ā—ā—Ä–į–Ĺ–Ķ —ė–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–ļ–ł –≥–Ķ–Ĺ–Ķ—Ä–ł—Ā–į–Ĺ–į, —Ā–į–≤—Ä—ą–Ķ–Ĺ–į —Ā–Ķ–Ī–ł —Ā–Ľ–ł—á–Ĺ–į —Ā–Ľ–ł–ļ–į –Ņ–į–Ņ—Ä–į—ā–ł, –ļ–ĺ—ė–į –∑–Ĺ–į—á–į—ė–Ĺ–ĺ –Ľ–ł—á–ł –Ĺ–į –Ņ—Ä–ł—Ä–ĺ–ī–Ĺ—É –Ņ–į–Ņ—Ä–į—ā. –ě—Ā—ā–į–Ľ–Ķ –Ī–ł—ô–ļ–Ķ, –ļ–į–ĺ —ą—ā–ĺ —Ā—É —Ä–ł–ľ—Ā–ļ–ł –Ī—Ä–ĺ–ļ–ĺ–Ľ–ł, –Ņ–ĺ–ļ–į–∑—É—ė—É —Ā–Ĺ–į–∂–Ĺ—É —Ā–į–ľ–ĺ—Ā–Ľ–ł—á–Ĺ–ĺ—Ā—ā.
–£ –ľ—É–∑–ł—Ü–ł
–í–ł–ī–ł —ė–ĺ—ą
–†–Ķ—Ą–Ķ—Ä–Ķ–Ĺ—Ü–Ķ
–°–Ņ–ĺ—ô–į—ą—ö–Ķ –≤–Ķ–∑–Ķ