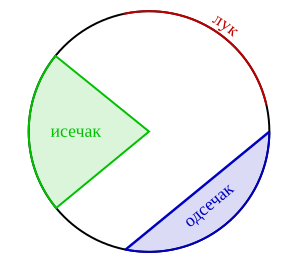
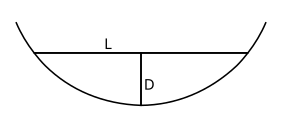
Круг
|
Read other articles:

Untuk lagu Scarling., lihat Crispin Glover (lagu). Crispin GloverGlover pada April 2012Lahir20 April 1964 (umur 59)New York City, New York, ASTempat tinggalLos Angeles, California, ASRepublik CekoPekerjaanAktor, sutradaraTahun aktif1977–sekarangSitus webcrispinglover.com Crispin Hellion Glover (lahir 20 April 1964) adalah seorang aktor dan sutradara asal Amerika Serikat. Glover dikenal karena memerankan karakter-karakter eksentrik di layar lebar, seperti George McFly dalam Back to...

Katedral RēzekneKatedral Hati KudusLatvian: Rēzeknes Vissvētākās Jēzus Sirds Romas katoļu katedrālecode: lv is deprecated Katedral RēzekneLokasiRēzekneNegara LatviaDenominasiGereja Katolik RomaArsitekturStatusKatedralStatus fungsionalAktifAdministrasiKeuskupanKeuskupan Rēzekne-Aglona Katedral Rēzekne atau yang bernama resmi Katedral Hati Kudus[1] (Latvian: Rēzeknes Vissvētākās Jēzus Sirds Romas katoļu katedrālecode: lv is deprecated ) adalah sebuah gereja kated...

Long Island Rail Road station in Suffolk County, New York GreenlawnGreenlawn stationGeneral informationLocationSuffolk CR 86 (Broadway) & Boulevard AvenueGreenlawn, New YorkCoordinates40°52′7.17″N 73°21′46.70″W / 40.8686583°N 73.3629722°W / 40.8686583; -73.3629722Owned byLong Island Rail RoadPlatforms2 side platformsTracks2Connections Huntington Area Rapid Transit: H30ConstructionParkingYes; Free and Residential permitsBicycle facilitiesYesAccessibleYes...
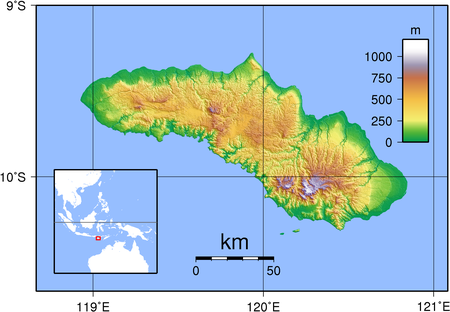
SumbaPulau Sumba dilihat dari Stasiun Luar Angkasa InternasionalGeografiLokasiAsia TenggaraKoordinat9°40′S 120°00′E / 9.667°S 120.000°E / -9.667; 120.000KepulauanKepulauan Nusa TenggaraLuas11.153 km2Peringkat luas73PemerintahanNegaraIndonesiaProvinsiNusa Tenggara TimurKota terbesarWaingapu (10.700 jiwa)KependudukanPenduduk685.186 jiwa (2010)Kepadatan61 jiwa/km2 Peta Pulau Sumba tahun 1925 Pulau Sumba adalah sebuah pulau di Provinsi Nusa T...

Kucumbu Tubuh IndahkuPoster rilis resmiSutradaraGarin NugrohoProduserIfa IsfansyahDitulis olehGarin NugrohoPemeran Muhammad Khan Raditya Evandra Randy Pangalila Sujiwo Tejo Teuku Rifnu Wikana SinematograferGay Hian TeohPenyuntingGreg AryaPerusahaanproduksiFourcolours FilmsGo-StudioTanggal rilis 13 Desember 2018 (2018-12-13) (Jogja-NETPAC Asian Film Festival) 18 April 2019 (2019-04-18) Durasi107 menit (21+)106 menit (17+)Negara IndonesiaBahasaIndonesia Kucumbu Tubuh Indahku adala...

دوكلاس هارتري معلومات شخصية اسم الولادة (بالإنجليزية: Douglas Rayner Hartree) الميلاد 27 مارس 1897 [1][2] كامبريدج الوفاة 12 فبراير 1958 (60 سنة) [1][2] كامبريدج سبب الوفاة قصور القلب مواطنة المملكة المتحدة عضو في الجمعية الملكية، وجمعية مانشستر الأد�...

Family fantasy TV show on BYUtv Ruby and the WellGenreFantasyCreated byLeeAnne H. Adams & Brian J. AdamsStarring Zoe Wiesenthal Kristopher Turner Joel Oulette Lina Sienna Dylan Kingwell Nobahar Dadui Paula Boudreau Music byLora Bidner & Robert CarliCountry of originUnited StatesCanadaOriginal languageEnglishNo. of seasons3No. of episodes28ProductionExecutive producers LeeAnne H. Adams Brian J. Adams Suzanne Bolch Scott Garvie Christina Jennings Anne Loi John May Jennifer McCann Andra ...

Contre-la-montre par équipes masculin aux championnats du monde de cyclisme sur route 2015 L'équipe BMC Racing championne du mondeGénéralités Sport Cyclisme sur route Organisateur(s) UCI Éditions 4e édition Lieu(x) Richmond Date 20 septembre 2015 Épreuves Contre-la-montre par équipes Palmarès Vainqueur BMC Racing Navigation Ponferrada 2014 Doha 2016 modifier Le contre-la-montre par équipes de marques masculin aux championnats du monde de cyclisme sur route 2015 a lieu le 20 s...

American social psychologist and writer Devon PriceBornMiddleburg Heights, Ohio, U.S.Alma materOhio State UniversityLoyola University ChicagoScientific careerFieldsSocial psychologyInstitutionsLoyola University Chicago Devon Price is an American social psychologist, blogger, and author focusing on autism. He is best known for his books, Unmasking Autism: Discovering the New Faces of Neurodiversity and Laziness Does Not Exist, as well as for publishing shorter pieces on Medium and Psychol...

Hormone Chorionic gonadotropin,alpha polypeptideIdentifiersSymbolCGAAlt. symbolsFSHA, GPHa, GPHA1, HCG, LHA, TSHANCBI gene1081HGNC1885OMIM118850RefSeqNM_000735UniProtP01215Other dataLocusChr. 6 q14-q21Search forStructuresSwiss-modelDomainsInterPro chorionic gonadotropin,beta polypeptideIdentifiersSymbolCGBAlt. symbolsCGB3NCBI gene1082HGNC1886OMIM118860RefSeqNM_000737UniProtP01233Other dataLocusChr. 19 q13.3Search forStructuresSwiss-modelDomainsInterPro Human chorionic gonadotropin (hCG) is a ...

L'expression « enlèvement international d'enfant » vient du droit international privé : elle renvoie au déplacement illégal d'un enfant depuis son domicile par une connaissance ou un membre de la famille vers un autre pays. Dans ce contexte, « illégal » signifie habituellement « en infraction au droit de garde » et le « domicile » est la résidence habituelle (en) de l'enfant. Ainsi que le laisse entendre « infraction au...

Pour les articles homonymes, voir Comté de Middlesex et Middlesex (homonymie). Middlesex Administration Pays Royaume-Uni Nation Angleterre Statut Comté traditionnel Géographie modifier Le Middlesex est un ancien comté traditionnel d'Angleterre. Il a le statut de comté administratif de 1889 à 1965, ancienne subdivision administrative d'Angleterre. La capitale en est alors Brentford. Il est aussi abrégé Middx. Toponymie Souvenir de l'établissement de peuples saxons dans l'ancien...

2013 copyright case in the United States Cariou v. PrinceCourtUnited States Court of Appeals for the Second CircuitCitation(s)714 F.3d 694Case historyPrior history784 F. Supp. 2d 337 (S.D.N.Y. 2011).Court membershipJudge(s) sittingBarrington Daniels Parker Jr., Peter W. Hall, J. Clifford Wallace (9th Cir.)Case opinionsMajorityParker, joined by HallConcur/dissentWallace Cariou v. Prince, 714 F.3d 694 (2d Cir. 2013)[1] is a copyright case of the United States Court of Appeals for the Se...

العلاقات النمساوية البلغارية النمسا بلغاريا النمسا بلغاريا تعديل مصدري - تعديل العلاقات النمساوية البلغارية هي العلاقات الثنائية التي تجمع بين النمسا وبلغاريا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقا...

Puerto Rican politician Herman BadilloMember of theU.S. House of Representativesfrom New YorkIn officeJanuary 3, 1971 – December 31, 1977Preceded byJacob H. GilbertSucceeded byRobert GarciaConstituency22nd district (1971–1973)21st district (1973–1977)8th Borough President of The BronxIn officeDecember 28, 1965 – December 31, 1969Preceded byJoseph F. PericoniSucceeded byRobert Abrams Personal detailsBorn(1929-08-21)August 21, 1929Caguas, Puerto RicoDiedDecember 3, 201...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Villafáfila – news · newspapers · books · scholar · JSTOR (May 2024) (Learn how and when to remove this message) Place in Castile and León, SpainVillafáfila FlagSealCountry SpainAutonomous community Castile and LeónProvince ZamoraMunicipality...

Voce principale: Eccellenza 1998-1999. Eccellenza Trentino-Alto Adige(DE) Oberliga Trentino-Südtirol1998-1999 Competizione Eccellenza Trentino-Alto Adige Sport Calcio Edizione 8ª Organizzatore FIGC - LNDComitato Regionale Trentino-Alto Adige Luogo Italia Partecipanti 16 Cronologia della competizione 1997-1998 1999-2000 Manuale Il campionato di Eccellenza Trentino-Alto Adige 1998-1999 è stato l'ottavo organizzato in Italia. Rappresenta il sesto livello del calcio italiano. Questo è ...

Mexican association football club This section is about the Mexican football club. For the Women's football club, see Club América (women). For other uses, see Club América (disambiguation) and América Football Club. Football clubAméricaFull nameClub de Fútbol América S.A. de C.V.Nickname(s)Águilas (Eagles)[1]Azulcremas (Bluecreams)[2]Millonetas (Millionaires)[2]Short nameAME[3]Founded12 October 1916; 107 years ago (1916-10-12)GroundEst...

Nikica ValentićValentić pada Mei 2011 Perdana Menteri KroasiaMasa jabatan3 April 1993 – 7 November 1995PresidenFranjo TuđmanPendahuluHrvoje ŠarinićPenggantiZlatko Mateša Informasi pribadiLahir(1950-11-24)24 November 1950Gospić, PR Croatia, FPR YugoslaviaMeninggal3 Mei 2023(2023-05-03) (umur 72)Zagreb, KroasiaPartai politikPersatuan Demokrat KroasiaSuami/istriAntoneta ValentićAnakIvanMarijaAlma materUniversitas ZagrebPekerjaanPolitikuspengacarapengusahaSunting kotak inf...

Canadian swimmer (born 1993) Katerine SavardKaterine Savard in 2013Personal informationNational teamCanadaBorn (1993-05-26) May 26, 1993 (age 31)Pont-Rouge, Quebec, CanadaHeight1.67 m (5 ft 6 in)Weight54 kg (119 lb)SportSportSwimmingStrokesButterfly, freestyleClubClub Aquatique Montreal CAMO Medal record Women's swimming Representing Canada Event 1st 2nd 3rd Olympic Games 0 0 1 World Championships (LC) 0 1 3 World Championships (SC) 4 3 2 Total 4 4 6 Olympic...