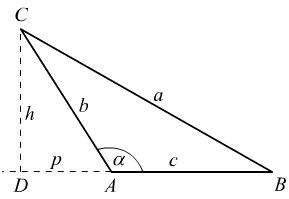
Косинусна теорема
|
Read other articles:

Black Hawk DownPoster film Black Hawk DownSutradaraRidley ScottProduserJerry BruckheimerRidley ScottDitulis olehKen NolanBerdasarkanBlack Hawk Down: A Story of Modern Waroleh Mark BowdenPemeranJosh HartnettEwan McGregorTom SizemoreEric BanaWilliam FichtnerEwen BremnerSam ShepardNikolaj Coster-WaldauPenata musikHans ZimmerSinematograferSławomir IdziakPenyuntingPietro ScaliaPerusahaanproduksiRevolution StudiosJerry Bruckheimer FilmsScott Free ProductionsDistributorColumbia PicturesTangga...

Lokasi Pusaran Ross di Laut Ross Pusaran Ross adalah satu dari dua pusaran yang terdapat di Samudra Selatan. Pusaran ini terletak di Laut Ross dan berputar searah jarum jam. Pusaran ini terbentuk oleh interaksi antara Arus Lingkar Kutub Antarktika dan Landas Benua Antarktika. Es laut diketahui terbentuk di bagian tengah pusaran ini.[1] Beberapa bukti menunjukkan bahwa pemanasan global menyebabkan penurunan keasinan air di Pusaran Ross sejak 1950-an.[2] Lihat pula Arus samudra ...

Betawi Punye RepperAlbum studio karya KojekDirilis16 Agustus 2012Genrerap, hip hopLabelRoyal Prima MusikindoProduserWizzowKronologi Kojek -String Module Error: Match not foundString Module Error: Match not found Betawi Punya Repper (2012) -String Module Error: Match not foundString Module Error: Match not found Betawi Punya Repper merupakan sebuah album musik perdana karya rapper Indonesia asal Betawi, Kojek. Daftar lagu Judulnye Kojek (Intro) (feat. Wizzow) Enjoy Jakarte Museum Bajaj Ciy...

Bupati Nias UtaraLambang Kabupaten Nias UtaraPetahanaAmizaro Waruwusejak 26 April 2021Masa jabatan5 tahunDibentuk2008Pejabat pertamaEdward ZegaSitus webniasutarakab.go.id Berikut ini adalah daftar Bupati Nias Utara. No Bupati Mulai menjabat Akhir menjabat Periode Wakil Bupati Ket. Fönaha Zega 2008 2011 1 Edward Zega 12 April 2011 12 April 2016 1 Fangato Lase 2 Marselinus Ingati Nazara 22 April 2016 22 April 2021 2(2015) Haogösöchi Hulu 3 Amizaro Waruwu 26 April 2021 Petahana 3(2020) Y...

Kali BuaranKali BoearanKali Buaran (K. Buaran) sebelah kanan tengah pada Peta Tata Air Jakarta (2012)Lokasi mulut sungaiTampilkan peta JawaKali Buaran (Indonesia)Tampilkan peta IndonesiaLokasiNegaraIndonesiaProvinsiJakartaCiri-ciri fisikHulu sungai - lokasiSungai Bekasi dan Sungai Cileungsi, Jawa Barat (hulu sumber dari Jonggol, Bogor) Muara sungaiBanjir Kanal Timur - koordinat6°11′01″S 106°55′44″E / 6.183590°S 106.928874°E / -6.18...

العلاقات الباكستانية الفرنسية باكستان فرنسا باكستان فرنسا تعديل مصدري - تعديل العلاقات الباكستانية الفرنسية هي العلاقات الثنائية التي تجمع بين باكستان وفرنسا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقار...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2016. PT. Dynap...

Commercial AM radio station in Los Angeles, California This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: KFWB – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this template message) KFWBLos Angeles, CaliforniaUnited StatesBroadcast areaGreater Los AngelesFrequency980 k...

Luis de Narváez (Granada, 1500 – 1555/1560) è stato un compositore spagnolo, principalmente di musica polifonica vocale e soltanto di poche musiche per vihuela, per le quali è più conosciuto al giorno d'oggi. La vihuela era uno strumento a corde pizzicate, fiorito principalmente in Spagna dal XV al XVII secolo, simile alla moderna chitarra, accordato come un liuto e molto diffuso in Spagna, dove prese il posto dello stesso liuto. Indice 1 Biografia 2 Bibliografia 3 Altri progetti 4 Coll...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

Peruvian surfer (born 1983) Sofía MulánovichMulánovich in July 2007Personal informationBornSofía Mulánovich Aljovín (1983-06-24) 24 June 1983 (age 40)Punta Hermosa, Lima, PeruResidenceCaballeros, Punta HermosaHeight5 ft 4 in (163 cm)Weight127 lb (58 kg)Surfing careerBest year2004 – ASP World ChampionCareer earnings$468,100SponsorsRoxy, Red Bull, Movistar, Reef, Al Merrick, LAN airlineMajor achievementsSurfers Hall of Fame inductee 2004, 2019 ISA World Sur...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Puerto Rican baseball player (born 1980) For other people with the same name, see Felipe López (disambiguation). Baseball player Felipe LópezLópez with the Tampa Bay RaysInfielderBorn: (1980-05-12) May 12, 1980 (age 44)Bayamón, Puerto RicoBatted: SwitchThrew: RightMLB debutAugust 3, 2001, for the Toronto Blue JaysLast MLB appearanceAugust 20, 2011, for the Milwaukee BrewersMLB statisticsBatting average.264Home runs90Runs batted in439 Teams Toronto Blue J...

NeanderthalRentang fosil: Pleistosen Kerangka Manusia Neanderthal, AMNH Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Mammalia Ordo: Primates Famili: Hominidae Genus: Homo Spesies: H. neanderthalensis Nama binomial Homo neanderthalensisKing, 1864 Sinonim Palaeoanthropus neanderthalensisH. s. neanderthalensis Linimasa homininKotak ini: lihatbicarasunting−10 —–−9 —–−8 —–−7 —–−6...

American opera singer Reed MillerBornJames Reed Miller(1880-02-29)February 29, 1880South Carolina, U.S.DiedDecember 29, 1923(1923-12-29) (aged 43)New York, U.S.Other namesJames ReedOccupationSingerSpouseNevada Van der VeerChildren1 Miller singing The Lost Chord by Arthur Sullivan (1913) James Reed Miller (February 29, 1880 – December 29, 1923), who recorded as Reed Miller and as James Reed, was an American tenor who had an active career as a concert and oratorio singer during ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Giorgio album – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this message) 1970 studio album by Giorgio MoroderGiorgioStudio album by Giorgio MoroderReleased1970Recorded1970Genre Psychedelic rock LabelFer...

1921 film FootlightsSurviving film posterDirected byJohn S. RobertsonWritten byRita Weiman (story)Josephine Lovett (scenario)Produced byFamous Players–LaskyStarringElsie FergusonReginald DennyMarc McDermottCinematographyRoy OverbaughDistributed byParamount PicturesRelease date September 1, 1921 (1921-09-01) Running time70+ minutes at (7078 feet)CountryUnited StatesLanguageSilent (English intertitles) Footlights is a 1921 American silent film romantic drama directed by John S....

Para otros usos de este término, véase Dinamarca (desambiguación). DinamarcaDanmark (danés) Nación constituyente del Reino de DinamarcaEstado miembro de la Unión EuropeaBandera Escudo Lema: Forbundne, forpligtet, for Kongeriget Danmark(en danés: 'Unidos, comprometidos, por el Reino de Dinamarca') [1] Himno: Der er et yndigt land(en danés: 'Hay un país hermoso')noiconHimno real: Kong Christian stod ved højen mast(en danés: 'El rey Cristián estaba al lado del palo m...

Swedish politician (born 1955) Kerstin LundgrenCKerstin Lundgren in October 2013Third Deputy Speaker of the RiksdagIncumbentAssumed office 24 September 2018SpeakerAndreas NorlénPreceded byEsabelle DingizianMember of the RiksdagIncumbentAssumed office 2002ConstituencyStockholm County Personal detailsBorn (1955-01-14) 14 January 1955 (age 69)Kramfors, SwedenPolitical partyCentre PartyAlma materUppsala University Kerstin Lundgren at Stockholm Pride 2019 Kerstin Margareta Lundgren (...

English linguist (1845–1912) Henry SweetBorn15 September 1845LondonDied30 April 1912(1912-04-30) (aged 66)OxfordNationalityBritishAlma materBalliol CollegeScientific careerFieldsPhonetics, Old English, language teachingInstitutionsEarly English Text Society, Philological Society, Oxford University Henry Sweet (15 September 1845 – 30 April 1912) was an English philologist, phonetician and grammarian.[1][2] As a philologist, he specialized in the Germanic languages...