Данијел Бернули
| |||||||||||||||||||||||
Read other articles:

Untuk pendahulunya, lihat DuPont (1802–2017). Untuk yang dipisahkan pada tahun 2019, lihat Dow Inc. dan Corteva. DuPont de Nemours, Inc.JenisPublikKode emitenNYSE: DDKomponen S&P 100Komponen S&P 500ISINUS26614N1028IndustriBahan kimiaPendahuluDow ChemicalE. I. du Pont de Nemours and CompanyDidirikan1 September 2017; 6 tahun lalu (2017-09-01)KantorpusatWilmington, Delaware, Amerika SerikatWilayah operasiSeluruh duniaTokohkunciEdward D. Breen(Chairman Eksekutif & CEO)Pendapata...
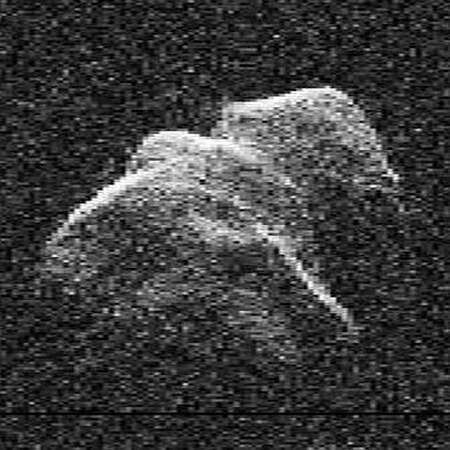
4179 ToutatisPenemuanDitemukan olehC. PollasSitus penemuan010Tanggal penemuan1989/01/04Ciri-ciri orbitAphelion4.129Perihelion0.937Sumbu semimayor2.533Eksentrisitas0.630Anomali rata-rata86.4Inklinasi0.4Bujur node menaik124.4Argumen perihelion278.8Ciri-ciri fisikMagnitudo mutlak (H)15.30 4179 Toutatis (1989 AC) adalah sebuah asteroid. Asteroid ini merupakan bagian dari asteroid Apollo, yang terletak dekat dengan bumi. Eksentrisitas orbit asteroid ini tercatat sebesar 0....

Chronologies Données clés 1573 1574 1575 1576 1577 1578 1579Décennies :1540 1550 1560 1570 1580 1590 1600Siècles :XIVe XVe XVIe XVIIe XVIIIeMillénaires :-Ier Ier IIe IIIe Chronologies thématiques Art Architecture, Arts plastiques (Dessin, Gravure, Peinture et Sculpture), Littérature et Musique classique Ingénierie (), Architecture et () Politique Droit Religion (,) Science Santé et médecine &...

The Type 19 Infantry Fighting Vehicle[1] (Chinese: 19式步兵战车; pinyin: Yāo jiǔ shì bùbīng zhàn chē) is a family of eight-wheeled amphibious, modular armored vehicle of the People's Republic of China. It improves upon and replaces the Type 08 wheeled armored vehicle family.[2] History and development In June 2020, a new type of 8x8 armored was observed in development to replace the Type 08 wheeled armored vehicle.[3] In 2023, the vehicle entered se...

Japanese anime television series Not to be confused with Concrete Revolution. Concrete Revolutio:Superhuman Phantasmagoriaコンクリート・レボルティオ~超人幻想~(Konkurīto Reborutio: Chōjin Gensō)GenreSuperhero[1]Created byBonesShō Aikawa Anime television seriesDirected bySeiji MizushimaProduced byYoshihiro ŌyabuMinoru TakanashiHirotaka KanekoHirotsugu OgisuRyōsuke NakajiTsutomu YanagimuraTakuya HosakaWritten byShō AikawaMasaki TsujiMusic&#...

Village and municipality in Slovakia Košice-okolie District in the Kosice Region Bočiar (Hungarian: Bocsárd) is a village and municipality in Košice-okolie District in the Košice Region of eastern Slovakia. History In historical records the village was first mentioned in 1249. Geography The village lies at an altitude of 210 metres and covers an area of 4.721 km2. It has a population of about 220 people. Genealogical resources The records for genealogical research are available at t...

Pemilihan umum anggota Dewan Perwakilan Daerah untuk Provinsi Provinsi Kalimantan Selatan 20242019202914 Februari 2024Suara terhitung62.28%per 25 Februari 2024 19:01 WIB (UTC+07:00)Kandidat Calon Zakaria Bahasyim Muhammad Hidayatollah Suara rakyat 232.148 164.782 Persentase 21.33% 15.14% Calon Gusti Farid Hamid Abdullah Suara rakyat 141.065 135.907 Persentase 12.96% 12.49% Pemilihan umum anggota Dewan Perwakilan Daerah untuk Provinsi Kalimantan Selatan 2024 disel...

Election in Utah Main article: 1952 United States presidential election 1952 United States presidential election in Utah ← 1948 November 4, 1952[1] 1956 → All 4 Utah votes to the Electoral College Nominee Dwight D. Eisenhower Adlai Stevenson Party Republican Democratic Home state New York[2] Illinois Running mate Richard Nixon John Sparkman Electoral vote 4 0 Popular vote 194,190 135,364 Percentage 58.93% 41.07% County Results E...

Pour les articles homonymes, voir Chapultepec (homonymie). Chapultepec Le monument des enfants héros. Géographie Pays Mexique Délégation Miguel Hidalgo Commune Mexico Superficie 6,86 km2 Localisation Coordonnées 19° 25′ 03″ nord, 99° 11′ 25″ ouest Géolocalisation sur la carte : Mexico Géolocalisation sur la carte : Mexique modifier Chapultepec est une colline et un grand parc, située à quelques kilomètres au sud-ouest du ...

Voci principali: XV Giochi olimpici invernali, Sci alpino ai Giochi olimpici. Sci alpinoCalgary 1988 Informazioni generaliLuogoNakiska Periodo15-27 febbraio Partecipanti272 da 43 nazioni Edizione precedente e successiva Sarajevo 1984 Albertville 1992 Le gare di sci alpino ai XV Giochi olimpici invernali di Calgary 1988 si disputarono dal 15 al 27 febbraio sulle piste di Nakiska; il programma incluse gare di discesa libera, supergigante, slalom gigante, slalom speciale e combinata,...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

Branch of the Michigan state government overseeing prisons and the parole and probation population This article may rely excessively on sources too closely associated with the subject, potentially preventing the article from being verifiable and neutral. Please help improve it by replacing them with more appropriate citations to reliable, independent, third-party sources. (June 2022) (Learn how and when to remove this message) Law enforcement agency Department of CorrectionsSeal of the Michig...

Japanese political term Part of a series onConservatism in Japan Ideologies Capitalist Fiscal State Corporate Nationalist Minzoku Populist Shōwa Statism Ultra Neo Paternalistic Religious State Shinto Ultra Principles Anti-communism Asian values Authority Bushido Discipline Duty Elitism Aristocracy Meritocracy Familialism Filial piety Heroism Hierarchy Kokutai Law and order Loyalty Militarism Monarchism Patriotism Racism Shinto Social order Sovereignty Tradition History 1955 System Aben...

Questa voce sull'argomento calciatori polacchi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Aleksander KłakNazionalità Polonia Altezza186 cm Calcio RuoloPortiere CarrieraSquadre di club1 1985-1992 Igloopol Dębica32 (-?)1993 Olimpia Poznań15 (-?)1993-1995 Górnik Zabrze37 (-?)1995 Straelen? (-?)1995 Homburg? (-?)1996 Bonner? (-?)1996-2002 Anversa? (-?)2002-...

Overview of and topical guide to extraterrestrial life This article is one of a series on:Life in the universe Outline Planetary habitability in the Solar System Venus Earth Mars Europa Enceladus Titan Life outside the Solar System Potentially habitable exoplanets Galactic habitable zone Habitability of... Binary star systems Natural satellites Neutron star systems Red dwarf systems K-type main-sequence star systems Yellow dwarf systems F-type main-sequence star systems vte The following outl...

French pop-rock singer and songwriter (born 1948) This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Hubert-Félix Thiéfaine – news · newspapers · books · scholar · JSTOR (July 2009) (Learn how an...

Not to be confused with the 2018 United States Senate election in Florida. 2018 Florida Senate election ← 2016 November 6, 2018 2020 → 22 of the 40 seats in the Florida Senate(and 2 special elections)21 seats needed for a majority Majority party Minority party Leader Bill Galvano Oscar Braynon Party Republican Democratic Leader since November 29, 2016 November 21, 2016 Leader's seat 10th 35th Last election 25 15 Seats before 24 16 Seats...

Being or thing in Germanic languages This article is about the term in Germanic languages. For the island in England, see Isle of Wight. For other uses, see Wight (disambiguation). Page recording a charm against a dwarf, from the Lacnunga collection, in which the dwarf is referred to as a wiht.[1] A wight is a being or thing. This general meaning is shared by cognate terms in Germanic languages, however the usage of the term varies greatly over time and between regions. In Old English...

1826 cadet riot at the United States Military Academy This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Eggnog riot – news · newspapers · books · scholar · JSTOR (December 2021) The eggnog riot, sometimes known as the grog mutiny, was a riot that took place at the United States Military Academy in We...

В Википедии есть статьи о других людях с такой фамилией, см. Войтович. Леонтий Викторович Войтович Дата рождения 16 мая 1951(1951-05-16) или 1951[1] Место рождения Еманжелинск, Челябинская область, РСФСР, СССР Дата смерти 7 февраля 2023(2023-02-07) Страна СССР Украина Род&...






