Рачунање
|
Read other articles:

American judge Sidney BreeseChief Justice of the Illinois Supreme CourtIn office1873–1874Preceded byCharles B. LawrenceSucceeded byPinkney H. WalkerIn office1867–1870Preceded byPinkney H. WalkerSucceeded byCharles B. Lawrence15th Speaker of the Illinois House of RepresentativesIn officeJanuary 6, 1851 – January 3, 1853Preceded byZadok CaseySucceeded byJohn ReynoldsUnited States Senatorfrom IllinoisIn officeMarch 4, 1843 – March 3, 1849Preceded byRichard M. YoungSucce...

Swiss footballer (born 2000) Filip Stojilković Stojilković in 2023Personal informationDate of birth (2000-01-04) 4 January 2000 (age 24)Place of birth Zollikon, SwitzerlandHeight 1.85 m (6 ft 1 in)Position(s) ForwardTeam informationCurrent team 1. FC Kaiserslautern(on loan from Darmstadt 98)Number 25Youth career2010–2014 Zürich2014 Red Star2014–2018 Zürich2018–2019 HoffenheimSenior career*Years Team Apps (Gls)2017–2018 Zürich II 9 (1)2018–2019 Hoffenheim II ...

Peta Lokasi Provinsi Maluku di Indonesia Berikut adalah daftar kecamatan dan kelurahan di Provinsi Maluku, Indonesia. Provinsi Maluku terdiri dari 9 kabupaten, 2 kotamadya, 118 kecamatan, 35 kelurahan, dan 1.200 desa. Pada tahun 2017, jumlah penduduknya diperkirakan mencapai 1.842.933 jiwa dengan total luas wilayah 46.914,03 km².[1][2] No. Kode Kemendagri Kabupaten/Kota Ibukota Luas Wilayah (km²) Penduduk (jiwa) 2017 Kecamatan Kelurahan Desa 1 81.04 Kab. Buru Namlea 4.932,32...

Княжества и области белорусские и литовские на Большом гербе Российской империи. 1882. Шесть губерний Северо-Западного края Российской империи — карта, напечатанная между 1905—1910 гг. в издательстве газеты «Kurjer Litewski» и названная «Карта шести губерний Литвы и Белой Рус�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2019) يوزف هيشت معلومات شخصية الميلاد 14 ديسمبر 1891 [1][2][3] وودج الوفاة 19 يونيو 1951 (59 سنة) [4] الدائرة الخامسة عشرة في باريس الإقامة النروي�...
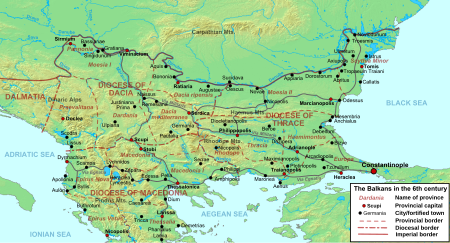
Dacia RipensisProvincia Dacia RipensisΔακία Παραποτάμιαcode: el is deprecated (Greek)Provinsi di Kekaisaran Romawic. 283 – 586 SPQR: Simbol Kekaisaran Romawi Balkan utara, termasuk Dacia Ripensis, pada abad k-6Ibu kotaRatiaria (sekarang di Vidin Province, Bulgaria)SejarahSejarah • Evakuasi Dacia Traiana, pembentukan Dacia Aureliana 271• Dacia Aureliana dipisahkan sebelum 285 Maseji 280s• Didevastasikan oleh invasi Avar 586 Didahului oleh Digan...

Part of a series on theCulture of Suriname Society History Language People race and ethnicity Religion Topics Cinema Cuisine Dance Literature Media Newspapers Radio Music Sports Symbols Flag Coat of arms Anthem Suriname portalvte Bellevue in Paramaribo (1989) The Cinema of Suriname is part of the Surinamese culture. National cinema, as a kind of artistic creativity, was born in the second half of the 70s of the 20th century. The first full-length film in Suriname was, shot in 1976, ...

Matuku came out of his caveIn Māori mythology, Matuku-tangotango (Matuku) is an ogre who kills Wahieroa the son of Tāwhaki.[1] In some versions, Matuku lives in a cave called Putawarenuku. Rātā, the son of Wahieroa, sets off to avenge his murdered father, and arrives at last at Matuku's village. He hears from Matuku's servant that at the new moon his master can be killed at the pool where he washes his face and hair.[2] When the new moon has come, Rātā waits until the og...

I'm Tee, Me TooThaiคนละทีเดียวกัน – I'm Tee, Me Too GenreSlice of lifeComedyPembuatGMMTVSutradaraNuttapong MongkolsawasPemeranAtthaphan PhunsawatPerawat SangpotiratPrachaya RuangrojTawan VihokratanaJumpol AdulkittipornThitipoom TechaapaikhunNegara asalThailandBahasa asliThaiJmlh. episode8ProduksiRumah produksiGMMTVRilis asliJaringanGMM 25AIS PlayRilis18 September (2020-09-18) –6 November 2020 (2020-11-6)Acara terkaitOur Skyy (Ep. 1, 4 dan 5)...

Scapolicomune Scapoli – Veduta LocalizzazioneStato Italia Regione Molise Provincia Isernia AmministrazioneSindacoRenato Sparacino (Crescere insieme) dal 7-6-2009 TerritorioCoordinate41°37′N 14°03′E / 41.616667°N 14.05°E41.616667; 14.05 (Scapoli)Coordinate: 41°37′N 14°03′E / 41.616667°N 14.05°E41.616667; 14.05 (Scapoli) Altitudine611 m s.l.m. Superficie18,94 km² Abitanti586[1] (31-12-2022) D...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

Giles MattheyLahirGiles Ingram Matthey11 November 1987 (umur 36)AustraliaPekerjaanPemeranTahun aktif2011–sekarang Giles Ingram Matthey (lahir 11 November 1987) adalah pemeran Britania Raya dikenal karena perannya sebagai Claude Crane dalam seri asli HBO True Blood, Gideon dalam seri ABC Once Upon a Time, dan Jordan Reed dalam seri FOX 24: Live Another Day. Karir Pada tahun 2012, ia dipilih untuk memerankan Claude Crane dalam seri HBO True Blood.[1] Referensi ^ 'True Blood...
NGO based in Toronto This article may have been created or edited in return for undisclosed payments, a violation of Wikipedia's terms of use. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. (April 2021) International Union of Food Science and TechnologyAbbreviationIUFoSTFormation1962; 62 years ago (1962)TypeINGOHeadquartersCanadaRegion served WorldwideOfficial language English, FrenchPresidentAman Wirakartakusumah[...

Equalities that involve trigonometric functions Trigonometry Outline History Usage Functions (sin, cos, tan, inverse) Generalized trigonometry Reference Identities Exact constants Tables Unit circle Laws and theorems Sines Cosines Tangents Cotangents Pythagorean theorem Calculus Trigonometric substitution Integrals (inverse functions) Derivatives Trigonometric series Mathematicians Hipparchus Ptolemy Brahmagupta al-Hasib al-Battani Regiomontanus Viète de Moivre Euler Fourier vte In...

Historia natural de los cuentos de miedo de Rafael Llopis Género Literatura de terrorEditorial Ediciones FuentetajaCiudad MadridPaís EspañaFecha de publicación 1974, 2013Páginas 384[editar datos en Wikidata] La Historia natural de los cuentos de miedo es una obra del psiquiatra, ensayista y traductor español Rafael Llopis, considerada el primer estudio sistemático sobre la literatura de terror publicado en España. La primera edición apareció a mediados de los años se...

Governing body of football and futsal in Belarus Football Federation of BelarusUEFAFounded1989HeadquartersMinskFIFA affiliation1992UEFA affiliation1993PresidentNikolay SherstnyovVice-PresidentYury VyarheychykWebsiteabff.by The Football Federation of Belarus (BFF; Belarusian: Беларуская федэрацыя футбола, romanized: Biełaruskaja Fiederacyja Futboła; Russian: Белорусская федерация футбола, romanized: Belorusskaya federatsiya futbo...

Motorsport track in Japan Fuji SpeedwayLocationOyama, Suntō District, Shizuoka Prefecture, JapanTime zoneUTC+09:00Coordinates35°22′18″N 138°55′36″E / 35.37167°N 138.92667°E / 35.37167; 138.92667Capacity110,000FIA Grade1OwnerToyota Motor Corporation (2000–present)Mitsubishi Estate Co. (1965–2000)OpenedDecember 1965; 58 years ago (1965-12)Re-opened: April 2005; 19 years ago (2005-04)ClosedSeptember 2003&...

Belgia padaOlimpiadeKode IOCBELKONKomite Olimpiade dan Interfederal BelgiaSitus webwww.olympic.be (dalam bahasa Belanda)Medali 59 55 45 Total 159 Penampilan Musim Panas1900190419081912192019241928193219361948195219561960196419681972197619801984198819921996200020042008201220162020Penampilan Musim Dingin192419281932193619481952195619601964196819721976198019841988199219941998200220062010201420182022Penampilan terkait lainnyaOlimpiade Interkala 1906 Belgia pada Olimpiade Musim Pana...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2016. Modifier Tone LettersJangkauanU+A700..U+A71F(32 titik kode)BidangBMPAksaraCommonSusunan simbolTanda nadaTerpakai32 titik kodeTak terpakai0 titik kode kosongRiwayat versi Unicode4.123 (+23)5.027 (+4)5.132 (+5) Catatan: [1] Modifier Tone Letters ad...

Place in Svalbard, NorwaySmeerenburgDutch-Danish whaling station (1619–1657)Ghost townSmeerenburgLocation in northwestern SvalbardCoordinates: 79°43′54″N 10°59′42″E / 79.73167°N 10.99500°E / 79.73167; 10.99500Country NorwaySysselSvalbardIslandSpitsbergenSettled1619Closure1657Population • Total0Time zoneUTC+1 (CET) • Summer (DST)+2 Remains of blubber ovens at Smeerenburg The train oil cookery of the Amsterdam chamber of the No...





























