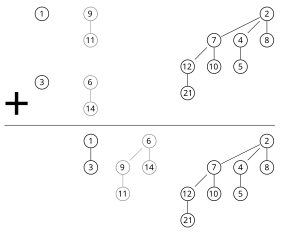
Биномни хип
|
Read other articles:

Religious educational institution For the LDS Church organization, see Sunday School (LDS Church). Sunday school, Manzanar War Relocation Center, 1943. Photographed by Ansel Adams. Baptist Sunday school group in Amherstburg, Ontario, [ca. 1910] A Sunday school is an educational institution, usually Christian in character and intended for children or neophytes. Sunday school classes usually precede a Sunday church service and are used to provide catechesis to Christians, especially children an...

English philologist Gabriel Turville-PetreTurville-Petre in 1972Born(1908-03-25)25 March 1908Leicestershire, EnglandDied17 February 1978(1978-02-17) (aged 69)Oxford, EnglandSpouse Joan Elizabeth Blomfield (after 1943)Children3, including Thorlac Turville-PetreAwardsGrand Knight's Cross of the Order of the Falcon (1963)Academic backgroundAlma mater Ampleforth College Christ Church, Oxford Academic advisors J. R. R. Tolkien Charles Leslie Wrenn Influe...

Pemandangan Ta' Qali dari Mdina Ta' Qali adalah sebuah lapangan terbuka di kawasan Attard di tengah Malta, yang terdiri dari stadion sepak bola nasional, Taman Nasional Ta' Qali, sebuah desa kerajinan, dan sebuah pasar sayuran nasional yang dikenal sebagai Pitkalija. Kedubes AS yang baru dibangun berada di seberang Taman Nasional Ta'Qali.[1] Pada Juli 2011, kedubes tersebut berpindah ke Ta'Qali dari Floriana dimana kedubes tersebut berdiri nyaris lima puluh tahun.[2] Referensi...

Eilif Peterssen 4 September 1852 – 29 Desember 1928 adalah seorang pelukis Norwegia. Ia terkenal karena seri lukisan pemandangan dan potretnya. Saat mulai terpengaruh oleh gaya impresionisme, ia sering diperbandingkan dengan Berthe Morisot.[1] Dalam tahun-tahun terakhir hidupnya, ia berkeliling Norwegia dan melukis berbagai pemandangan yang membuatnya terkenal. Masa kecil dan ringkasan karier Ia menghabiskan masa kecilnya di kompleks Hegdehauge, distrik Frogner. Ayahn...

Constituency of Bangladesh's Jatiya Sangsad BandarbanConstituencyfor the Jatiya SangsadDistrictRangamati Hill DistrictDivisionChittagong DivisionElectorate418,217 (2018)Current constituencyCreated1973PartyBangladesh Awami LeagueMember of ParliamentDipankar TalukdarPrev. ConstituencyKhagrachari (Constituency 298)Next ConstituencyBandarban (Constituency 300) Rangamati is a constituency of the Jatiya Sangsad (National Parliament) of Bangladesh,[1] represented, since 2018 June, by Dipanka...

Gran Premio delle NazioniSport Automobilismo CategoriaFormula AFormula 1 Paese Svizzera CadenzaAnnuale StoriaFondazione1946 Soppressione1950 Numero edizioni3 Record vittorie Nino Farina (2) Modifica dati su Wikidata · Manuale Il Gran Premio delle Nazioni è stata una corsa automobilistica di velocità in circuito. Indice 1 Storia 2 Albo d'oro 3 Altri progetti 4 Collegamenti esterni Storia Questa sezione sull'argomento automobilismo è ancora vuota. Aiutaci a scriverla! Albo d'...

Questa voce o sezione contiene informazioni riguardanti un evento futuro. Il contenuto potrebbe cambiare radicalmente non appena maggiori informazioni saranno disponibili. Per favore, non aggiungere speculazioni alla voce. Neomcittà(AR) نيوم Neom – Veduta LocalizzazioneStato Arabia Saudita ProvinciaTabuk AmministrazioneSindacoNadhmi Al-Nasr (direttore)[1] Data di istituzione24/10/2017 TerritorioCoordinate28°00′23″N 35°12′09″E / 28.006389°N 35.20...

Конкуренция уголовно-правовых норм имеет место в случаях, когда одно и то же деяние регулируется двумя нормами уголовного законодательства, из которых подлежит применению только одна. Содержание 1 Законодательные положения, касающиеся конкуренции уголовно-правовых но�...

Buddhist temple in Japan Taima-dera Taima-dera (當麻寺) is a Buddhist temple in Katsuragi, Nara, Japan. The temple legend says it was built originally in 612 by the Imperial Prince Maroko, the brother of Prince Shotoku. The temple was moved to its present location in 681 by the grandson of Prince Maroko, and served as the head temple, or honzan (本山) of the Hosso sect although currently the temple is jointly administrated by Shingon and Jodo schools. Taima Mandala(copy), Kamakura period...

Australia international rugby league footballer This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Paul Sironen – news · newspapers · books · scholar · JSTOR (September 2014) (Learn how and when to...

عبد الملك بن دعسين معلومات شخصية تاريخ الميلاد سنة 1545 الوفاة سنة 1597 (51–52 سنة) المخاء مواطنة اليمن الحياة العملية المهنة فقيه اللغات العربية تعديل مصدري - تعديل ابن دَعْسَيْن، عبد الملك بن عبد السلام بن عبد الحفيظ ابن دعسين الأموي القرشي (952 هـ/ 1545م ...

Trưởng ban Ban Dân vận Trung ươngĐảng Cộng sản Việt NamĐảng kỳ Đảng Cộng sản Việt NamĐương nhiệmBùi Thị Minh Hoàitừ 8 tháng 4 năm 2021Dinh thựsố 105B phố Quán Thánh, phường Quán Thánh, quận Ba Đình, Hà NộiBổ nhiệm bởiBan Chấp hành Trung ương Đảng Cộng sản Việt NamNhiệm kỳ5 nămNgười đầu tiên nhậm chứcXuân ThủyThành lập3/1976Website[www.danvan.vn/ Ban Dân vận Trung ương] Việt Na...

帕爾·拉扎爾出生1988年3月11日 (36歲)德布勒森 職業足球員 此生者传记没有列出任何参考或来源。 (2015年6月3日)请协助補充可靠来源,针对在世人物的无法查证的内容将被立即移除。 此條目需要擴充。 (2015年6月3日)请協助改善这篇條目,更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。 帕爾·拉扎爾(匈牙利語:Pál Lázár;198...

Gerhard BertholdNascitaSchneeberg, 12 marzo 1891 MorteJuchnov, 14 aprile 1942 Dati militariPaese servito Impero tedesco Repubblica di Weimar Germania nazista Forza armata Deutsches Heer Reichswehr Wehrmacht ArmaHeer Anni di servizio1913-1942 GradoGeneralleutenant (postumo) GuerrePrima guerra mondiale Seconda guerra mondiale fonti nel corpo del testo voci di militari presenti su Wikipedia Manuale Gerhard Berthold (Schneeberg, 12 marzo 1891 – Juchnov, 14 aprile 1942) è stato un ...
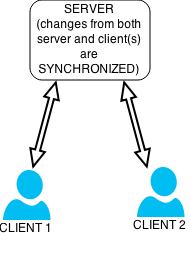
Consistency among data between source and target data stores Synchronization process between a server and two clients Data synchronization is the process of establishing consistency between source and target data stores, and the continuous harmonization of the data over time. It is fundamental to a wide variety of applications, including file synchronization and mobile device synchronization. Data synchronization can also be useful in encryption for synchronizing public key servers. Data sync...

Baja California Provincia 1804-1824 Localización de la provincia de Baja CaliforniaCapital LoretoEntidad Provincia • País Imperio español • Virreinato Nueva EspañaHistoria • 1804 División de Las Californias • 1824 Territorio de Baja California Precedido por Sucedido por ← ← → [editar datos en Wikidata] La provincia de Baja California fue un territorio del Virreinato de Nueva España y posteriormente del Primer Imperio mexicano. La provin...

For the linguistic term, see Inalienable possession. Part of a series onEconomic, applied, and development anthropology Basic concepts Commodification Barter Debt Finance Embeddedness Reciprocity Redistribution Value Wealth Gift economy Limited good Inalienable possessions Singularization (commodity pathway) Spheres of exchange Social capital Cultural capital Provisioning systems Hunting-gathering Pastoralism Nomadic pastoralism Shifting cultivation Moral economy Peasant economics Case studie...

2000 film by Jay Roach This article is about the 2000 film. For other uses, see Meet the Parents (disambiguation). Meet the ParentsTheatrical release posterDirected byJay RoachScreenplay by Jim Herzfeld John Hamburg Story by Greg Glienna Mary Ruth Clarke Based onMeet the Parentsby Greg GliennaMary Ruth ClarkeProduced by Nancy Tenenbaum Jay Roach Jane Rosenthal Robert De Niro Starring Robert De Niro Ben Stiller Blythe Danner Teri Polo James Rebhorn Jon Abrahams Owen Wilson CinematographyPeter ...

School of anarchist thought Part of a series onAnarchism Glossary History Outline Schools of thought Feminist Green Primitivist Social ecology Total liberation Individualist Egoist Market Naturist Philosophical Mutualism Postcolonial African Black Queer Religious Christian Jewish Social Collectivist Parecon Communist Magonism Without adjectives Methodology Counter-economics Illegalism Insurrectionary Pacifist Platformism Relationship Syndicalist Synthesis Theory Practice Anarchy Anarchist Bla...

Arsip 8 Desember 2008 – 20 September 2011 23 Desember 2011 – 9 November 2012 16 Agustus 2013 – 27 Mei 2014 Tenang... tenang... The Anti-Flame Barnstar Penghargaan ini diberikan untuk pengguna yang tetap tenang dalam konflik dan menyelesaikan masalah dengan damai. Terima kasih atas kesabaran dan pengertian yang telah anda buktikan terhadap permasalahan padanan frasa. Salam. -- Wagino 20100516 (bicara) 01:10, 22 September 2011 (UTC) Berkas tanpa lisensi Nominasi penghapusan Berkas:Anama ...