Hondrula

Hondrule v hondritu Grassland. Za primerjavo je dodamo milimetersko merilo.

Hondrula je okroglo zrno, ki ga lahko najdemo v hondritih. Beseda izvira iz grške besede hondros, kar pomeni zrno. Hondrule se nastajale kot raztaljene ali delno raztaljene kapljice v vesolju preden so vrasle v asteroide. Hondrule tako predstavljajo najstarejšo snov v Osončju. Verjetno so bile tudi osnovni material pri nastajanje planetov. V velikem številu jih najdemo v posebni skupini meteoritov, ki so jim dale ime hondriti. V meteoritih so vgrajene v drobnozrnato osnovo (matrica). Hondrule poznajo že od leta 1820, ko jih je opisal Jacques Louis de Bourbon (1751-1825) kot zanimive kroglice v meteoritih. Ime jim je dal leta 1869 Gustav Rose.

Nastanek hondrul

Hondrule predstavljajo nastarejšo snov v Osončju. Danes vemo, da so iz prvotne snovi, ki je bila zelo hitro segreta (1 minuto ali še manj) do temperature okoli 1900°C. Nastale so kroglice, ki so se ohladile v nekaj urah. Ni pa znan izvor energije, ki je povzročil taljenje. Prav tako ni znano, kje se je to dogajalo. Možno je tudi, da je sestavina osnovne snovi v kateri so hondrule, iz prav takšne snovi kot sestavljajo hondrule. Veliko teorij trdi., da so hondrule nastale že v oblaku, iz katerega je nastalo Sonce ali pa v protoplanetnem disku.

Pregled vsebnosti hondrul v skupinah hondritov

Skupina
hondritov		 količina
(vol%)		 povprečni premer
(mm)
CI 0 –
CM 20 0,3
CO 50 0,15
CV 45 1
CK 45 1
CR 50-60 0,7
CH 70 0,02
CB 20-40 10 (podskupina a),
0,2 (podskupina b)
H 60-80 0,3
L 60-80 0,7
LL 60-80 0,9
EH 60-80 0,2
EL 60-80 0,6
R >40 0,4
K 30 0,6

Glej tudi

Zunanje povezave

Read other articles:

Mie Sukses's

Mie Sukses'sJenis produkMi instanPemilikWings FoodNegara IndonesiaDiluncurkan2015Merek terkaitMie SedaapJargonRasanya Suksess, Lapernya BeressSitus webwingscorp.com/brand-detail/mie-suksess-isi-2/ Mie Sukses's adalah merek mi instan yang diproduksi oleh Wings Food. Diluncurkan pada tahun 2015. Produk ini adalah produk mi instan keluaran Wings Food yang kedua setelah Mie Sedaap yang diproduksi pada tahun 2003 silam.[1] Varian rasa Kuah Kari Ayam Ayam Bawang Soto Mie Goreng Ayam Kr...

 

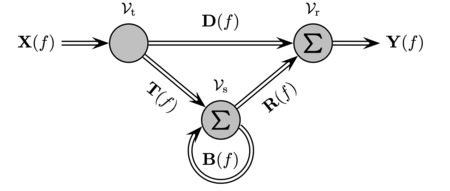
Propagation graph

Models signal dispersion by representing the radio propagation environment by a graph Example of a propagation graph with four transmitters (Tx1-Tx4), three receivers (Rx1-Rx3) and six scatterers S1-S6. An edge is drawn from one vertex to another if propagation is possible. Propagation graphs are a mathematical modelling method for radio propagation channels. A propagation graph is a signal flow graph in which vertices represent transmitters, receivers or scatterers. Edges in the graph model ...

 

Determinate

DeterminateSingel oleh Bridgit Mendler featuring Adam Hicksdari album Lemonade MouthDirilis15 April 2011 (2011-04-15)Direkam2010GenreSynth-popDurasi3:18LabelWalt DisneyPencipta Niclas Molinder Joacim Persson Johan Alkenäs Charlie Mason Ebony Burks Adam Hicks ProduserTwinKronologi singel Bridgit Mendler Somebody (2011) Determinate (2011) Breakthrough (2011) Kronologi singel Adam Hicks In the Summertime(2009) Determinate(2011) Breakthrough(2011) Determinate adalah lagu yang diba...

羅生門 (電影)

本條目存在以下問題，請協助改善本條目或在討論頁針對議題發表看法。 此條目需要补充更多来源。 (2018年3月17日)请协助補充多方面可靠来源以改善这篇条目，无法查证的内容可能會因為异议提出而被移除。致使用者：请搜索一下条目的标题（来源搜索：羅生門 (電影) — 网页、新闻、书籍、学术、图像），以检查网络上是否存在该主题的更多可靠来源（判定指引）。 �...

 

King Cup

Football tournamentThe Custodian of the Two Holy Mosques' CupOrganising bodySaudi Arabia Football Federation (SAFF)Founded1957; 67 years ago (1957)RegionSaudi ArabiaNumber of teams32Qualifier forAFC Champions League 2International cup(s)AFC Champions League 2Current championsAl-Hilal (10th title)Most successful club(s)Al-Ahli (13 titles)Television broadcastersShahid / SSC 2023–24 King Cup The King Cup (sometimes spelled King's Cup),[1] officially known as The Custo...

 

Kurt Tank

German aeronautical engineerThis article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Kurt Tank – news · newspapers · books · scholar · JSTOR (January 2013) (Learn how and when to remove this template message) Kurt Waldemar TankProf. Dr. Dipl.-Ing. Kurt Tank, March 1941Born(1898-02-24)24 February 1898Bromberg, Provinc...

Shamsher Gazi

Tiger of BhatiShamsher Ghaziশমসের গাজীBorn1712Kungura, Twipra KingdomDiedcirca 1760 (aged 47–48)Cause of deathCannon executionTermChakladar of RoshnabadPredecessorNasir MahmudSuccessorKrishna ManikyaParentsPeyar Muhammad Khan (father)Kaiyara Bibi (mother)Reinterpreted fort of Shamsher Ghazi at a resort in Southern Chhagalnaiya.Kingdom of TripuraPart of History of Tripura Kings of Tripura Maha Manikyac. 1400–1431Dharma Manikya I1431–1462Ratna Manikya...

 

Oleksii Krutykh

Ukrainian tennis player Oleksii KrutykhKrutykh at the 2023 French OpenCountry (sports) UkraineResidenceKyiv, UkraineBorn (2000-03-10) 10 March 2000 (age 24)Kyiv, UkraineHeight1.85 m (6 ft 1 in)PlaysRight-handed (two-handed backhand)Prize money$278,030SinglesCareer record3–4Career titles0Highest rankingNo. 160 (27 February 2023)Current rankingNo. 295 (25 December 2023)Grand Slam singles resultsAustralian Open1R (2023)French OpenQ2 (...

 

Karoshi

Sudden death from overwork For other uses, see Karoshi (disambiguation). Worked to death redirects here. For the killing method using forced labour, see Extermination through labour. A No More Karoshi protest in Tokyo, 2018 Deaths due to long working hours per 100,000 people (15+) Karoshi (Japanese: 過労死, Hepburn: Karōshi), which can be translated into overwork death, is a Japanese term relating to occupation-related sudden death.[1] The most common medical causes of karoshi dea...

DirecTV Stream

Streaming pay TV service provider DirecTV StreamFormerlyDirecTV Now (2016–2019)AT&T TV (2019–2021)Company typeDivisionIndustryPay televisionFoundedNovember 30, 2016; 7 years ago (2016-11-30)HeadquartersEl Segundo, California, United StatesArea servedUnited StatesServicesOTT Internet TelevisionParentDirecTVWebsitestreamtv.directv.com DirecTV Stream (formerly DirecTV Now and AT&T TV) is a family of streaming multichannel television services offered in the United St...

 

Demitasse

Small cup used to serve coffee Look up demitasse or demitazza in Wiktionary, the free dictionary. Demitasse set with metal frames and spoons A demitasse (/ˈdɛmɪtæs/; French: half cup), demi-tasse,[1] or espresso cup is a small cup used to serve espresso. It may also refer to the coffee served in such a cup, though that usage had disappeared in France by the early 20th century.[1] A demitasse typically has a capacity of approximately 60–90 millilitres (2–3 US&...

 

Hunab Ku

Hunab Ku (Mayan pronunciation: [huˈnaɓ kʼu], standard Yucatec Mayan orthography: Junab K'uj) is a colonial period Yucatec Maya reducido term meaning The One God. It is used in colonial, and more particularly in doctrinal texts, to refer to the Christian God. Since the word is found frequently in the Chilam Balam of Chumayel, a syncretistic document heavily influenced by Christianity, it refers specifically to the Christian God as a translation into Maya of the Christian concept of ...

國立嘉義高級工業職業學校

本條目存在以下問題，請協助改善本條目或在討論頁針對議題發表看法。 此條目已列出參考資料，但文內引註不足，部分內容的來源仍然不明。 (2023年3月13日)请加上合适的文內引註加以改善。 此條目或其章節极大或完全地依赖于某个单一的来源。 (2023年3月13日)请协助補充多方面可靠来源以改善这篇条目。致使用者：请搜索一下条目的标题（来源搜索：國立嘉義高級工業職�...

 

Cyprus Police

This article is about the police service of the Republic of Cyprus. For the police service in Northern Cyprus, see Directorate General for Police. Law enforcement agency Cyprus PoliceGreek: Αστυνομία ΚύπρουTurkish: Kıbrıs PolisCyprus police logoMottoΑνθρώπινη και Υπερήφανη(Humane and Proud)Agency overviewFormed1960Jurisdictional structureNational agencyCYOperations jurisdictionCYAbove: Northern part of the island currently not policed by the Republic of ...

 

توين ليكس

  لمعانٍ أخرى، طالع توين ليكس (توضيح). توين ليكس   الإحداثيات 43°33′35″N 93°25′23″W / 43.559722222222°N 93.423055555556°W / 43.559722222222; -93.423055555556   [1] تقسيم إداري  البلد الولايات المتحدة[2]  التقسيم الأعلى مقاطعة فريبورن  خصائص جغرافية  المساحة 1.326447 كيلومتر م...

خط صيني عربي

  هذه المقالة عن الخط الصيني، وهو أحد الخطوط العربية. لخط صيني (توضيح)، طالع خط صيني عربي (توضيح). جزء من سلسلة مقالات حولفن الخط عربي كوفي شرق آسيا ياباني صيني عربي كوري مغولي [الإنجليزية] تبيتي [الإنجليزية] فيتنامي [الإنجليزية] هندي [الإنجليزية] فارسي [الإنجليزية] جورجي �...

 

Shmuel Dayan

A questa voce o sezione va aggiunto il template sinottico {{Carica pubblica}} Puoi aggiungere e riempire il template secondo le istruzioni e poi rimuovere questo avviso. Se non sei in grado di riempirlo in buona parte, non fare nulla; non inserire template vuoti. Shmuel Dayan Shmuel Dayan (Žaškiv, 8 agosto 1891 – Nahalal, 11 agosto 1968) è stato un politico israeliano. Biografia Nato nell'attuale Ucraina - all'epoca parte dell'Impero russo - aderì da ragazzo al movi...

 

Piermarco Cannarsa

Piermarco Cannarsa (Roma, 21 febbraio 1957) è un matematico italiano. I suoi interessi scientifici comprendono l'analisi funzionale, le equazioni alle derivate parziali e la teoria dei controlli. Insieme a Carlo Sinestrari ha scritto il primo testo che si è occupato sistematicamente ed esaurientemente delle funzioni semiconcave.[1] Indice 1 Biografia 1.1 Incarichi 2 Opere 3 Note 4 Collegamenti esterni Biografia Si è laureato in Matematica nel 1979 presso l'Università di Pisa essen...

伏明霞

伏明霞个人资料出生 (1978-08-16) 1978年8月16日（45歲） 中国湖北省武汉市居住地 香港身高1.68米（5英尺6英寸）体重70公斤（154英磅）配偶梁錦松（2002年7月15日)运动国家／地区 中国运动跳水项目10米跳台 → 3米跳板前任搭档郭晶晶教练于芬退役1996年（1998年復出）2000年 奖牌记录 代表 中国 女子跳水 夏季奧林匹克運動會 1992年巴塞隆納 10米跳台 1996年亞特蘭大 10米...

 

Kōzuke

Questa voce o sezione sull'argomento Giappone non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Mappa delle province giapponesi con la provincia di Kozuke evidenziata. Kozuke, formalmente scritta come Kozuke no Kuni (giapponese: 上野国) fu una provincia del Giappone nella regione di Tosando, che oggi fa ...