INTLAB
|
Read other articles:

Akademi Musik Franz LisztLiszt Ferenc Zeneművészeti EgyetemJenisNegeriDidirikan1875RektorAndrea VighAlamat8 Liszt Ferenc tér Budapest, Hungaria 1061WarnaEmas dan biru langit Situs webzeneakademia.hu, lfze.hu Akademi Musik Franz Liszt (Hongaria: Liszt Ferenc Zeneművészeti Egyetemcode: hu is deprecated ) adalah universitas musik dan gedung konser di Budapest, Hungaria, didirikan pada 14 November 1875. Ini adalah rumah bagi Koleksi Liszt, yang menampilkan beberapa buku dan manus...

Lambang nasional Arab Saudi (Arab: شعار السعوديةcode: ar is deprecated ) digunakan tahun 1950.[1] Sesuai Konstitusi Saudi[2] lambang ini terdiri dari dua pedang yang bersilangan dengan sebatang pohon Kurma di ruang terbuka di antara pedang-pedang tersebut. Pedang-pedang melambangkan dua daerah, Hijaz dan Nejd yang disatukan di bawah Ibn Saud pada tahun 1926.[3] Catatan kaki ^ Flags of the World, Saudi Arabia page ^ Saudi Basic Law of Government, Article 4....

العلاقات الإسرائيلية الدومينيكانية إسرائيل جمهورية الدومينيكان إسرائيل جمهورية الدومينيكان تعديل مصدري - تعديل العلاقات الإسرائيلية الدومينيكانية هي العلاقات الثنائية التي تجمع بين إسرائيل وجمهورية الدومينيكان.[1][2][3][4][5] مقارنة ب...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (mars 2024). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références » En pratique : Quelles sources sont attendues ? Comme...
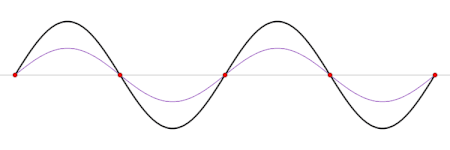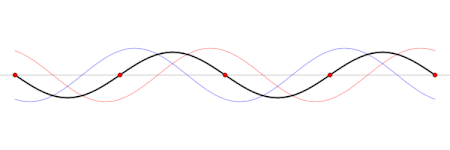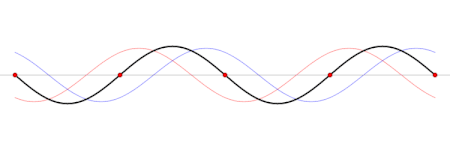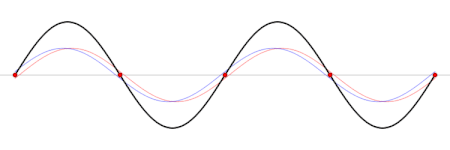
Gelombang berdiri (hitam) yang digambarkan sebagai penjumlahan dua gelombang yang merambat dengan arah yang saling berlawanan (biru dan merah). Seiche (/ˈseɪʃ/ SAYSH) adalah gelombang berdiri dalam sebuah perairan yang tertutup, baik terutup sepenuhnya maupun sebagian. Fenomena akibat seiche dapat terjadi di danau, waduk, kolam renang, teluk, pelabuhan, dan laut. Syarat utama terbentuknya seiche adalah adanya perairan yang setidaknya tertutup sebagian sehingga dapat menjadi tempat terbentu...

Species of cactus Sclerocactus whipplei Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Order: Caryophyllales Family: Cactaceae Subfamily: Cactoideae Genus: Sclerocactus Species: S. whipplei Binomial name Sclerocactus whipplei(Engelm. & J.M.Bigelow) Britton & Rose Sclerocactus whipplei, or Whipple's fishhook cactus,[1] is a cactus (family Cactaceae) found in the Colorado Plateau and Canyonlands region of the southwestern ...

Antireligious campaign in China Rep. Ileana Ros-Lehtinen, who co-sponsored a Congressional resolution condemning organ harvesting from Falun Gong adherents, speaks at a rally in Washington, D.C. Freedom of religion Concepts Laicism Religious discrimination Religious censorship Religious liberty Religious pluralism Secularism Separation of church and state Anti-clericalism School prayer Catholic priests in public office Confessionalism Theocracy State religion Secular state Confessional state ...

1950 British forced resettlement plan during the Malayan Emergency Photograph of a model new village, designed as part of the Briggs Plan to separate the largely Chinese Malaysian rural populace from communist guerrillas. Part of the Independence of Malaya Events Early Malay nationalism Kesatuan Melayu Muda • Defenders of the Homeland Japanese occupation of Malaya British Military Administration Malayan Union All-Malaya Council of Joint Action Federation of Malaya Sungai Sipu...

العلاقات الأردنية الناوروية الأردن ناورو الأردن ناورو تعديل مصدري - تعديل العلاقات الأردنية الناوروية هي العلاقات الثنائية التي تجمع بين الأردن وناورو.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة الأر�...

Shopping mall in Georgia, United States This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (September 2022) (Learn how and when to remove this template message) Plaza Fiesta vendor space, May 2013 Reli...

Звукорежиссёр за микшерным пультом во время перезаписи фонограммы Озву́чивание[1], озву́чение[2][3] (не «озвуча́ние»[4] и не «озвуче́ние»[4])[* 1] фильма — процесс записи звукового сопровождения фильма, осуществляемый отдельно от съёмки изображ...

2011 American documentary film Magic TripPromotional release posterDirected by Alex Gibney Alison Ellwood Produced by Alex Gibney Gareth Wiley Starring Ken Kesey Neal Cassady The Grateful Dead Jack Kerouac Allen Ginsberg The Merry Band of Pranksters Larry McMurtry Ken Babbs Timothy Leary Narrated byStanley TucciProductioncompanyHistory Channel FilmsDistributed byMagnolia PicturesRelease date August 5, 2011 (2011-08-05) Running time90 minutesCountryUnited StatesLanguageEnglish M...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Latin letter U with acute accent For the cuneiform sign, see Ú (cuneiform).Latin letter U with acute Ú, ú (u-acute) is a Latin letter used in the Czech, Faroese, Hungarian, Icelandic, Karakalpak and Slovak writing systems. This letter also appears in Dutch, Frisian, Irish, Occitan, Catalan, Pinyin, Portuguese, Spanish, Italian, Galician, and Vietnamese as a variant of the letter U.[1] Usage in various languages Czech Ú/ú is the 34th letter of the Czech alphabet and represents a /...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Band GeeksEpisode SpongeBob SquarePantsKartu judulNomor episodeMusim 2Episode 35SutradaraAaron SpringerPenulisC.H. GreenblattAaron SpringerMerriwether WilliamsMusikSweet VictoryTanggal siar7 September 2001Bintang tamu David Glen Eisley sebagai SpongeBob ketika menyanyikan lagu Sweet Victory Kronologi episode ← SebelumnyaThe Secret Box Selanjutnya →Graveyard Shift Daftar episode SpongeBob SquarePants Band Geeks adalah episode dari seri animasi SpongeBob SquarePants. Ia merup...

Christianity by country Africa Algeria Angola Benin Botswana Burkina Faso Burundi Cameroon Cape Verde Central African Republic Chad Comoros Democratic Republic of the Congo Republic of the Congo Djibouti Egypt Equatorial Guinea Eritrea Eswatini Ethiopia Gabon Gambia Ghana Guinea Guinea-Bissau Ivory Coast Kenya Lesotho Liberia Libya Madagascar Malawi Mali Mauritania Mauritius Morocco Mozambique Namibia Niger Nigeria Rwanda São Tomé and Príncipe Senegal Seychelles Sierra Leone Somalia South...

Artikel ini mungkin terdampak dengan peristiwa terkini: Invasi Rusia ke Ukraina 2022. Informasi di halaman ini bisa berubah setiap saat. Angkatan Bersenjata UkrainaЗбройні сили УкраїниZbroini syly UkrainyLambang Angkatan Bersenjata UkrainaBendera Angkatan Bersenjata UkrainaDidirikan29 Maret 1917Formasi terkini6 Desember 1991Angkatan Angkatan Darat Angkatan Udara Angkatan Laut Korps Marinir Pasukan Serangan Udara Pasukan Operasi Khusus Pasukan Pertahanan TeritorialMarkas besa...

Confection of sugar, honey and almond flour Marchpane redirects here. For other uses of marzipan and marchpane, see Marzipan (disambiguation). MarzipanPlain marzipan being rolled flatAlternative namesMarzapane, marchpaneTypeConfectioneryMain ingredientsAlmond meal, sugarVariationsPersipan, frutta martorana Media: Marzipan Marzipan is a confection consisting primarily of sugar and almond meal (ground almonds), sometimes augmented with almond oil or extract. It is often made into swee...

هذا الصندوق: اعرضناقشعدل اعرضناقشعدل لجميع البلدات (الحجم 7 أو أكبر) والمواقع الاستراتيجية مثل المطارات، والمعابر الحدودية، والموانئ، والسدود، والقواعد العسكرية، وحقول النفط. لجميع القرى (الحجم 6 أو أقل) ومواقع تفصيلية مثل التلال، والمصانع، والأحياء، ونقاط التفتيش. تنقس�...