Gregorijanski kalendar
|
Read other articles:

Hutan bakau Paparan SundaTaman Nasional Bako, Sarawak, MalaysiaTeritori kawasan ekologi (warna ungu)EkologiWilayahIndomalayaBiomaHutan bakauGeografiArea37,529 km2 (14,490 sq mi)NegaraMalaysia and IndonesiaKonservasiDilindungi13.16%[1]Hutan bakau Paparan Sunda adalah sebuah kawasan ekologi yang berada di bioma hutan bakau di pesisir pulau-pulau di Kalimantan dan Sumatera timur, di Malaysia dan Indonesia. Mereka menjadi tempat tinggal bekantan. Hutan bakau ini ber...

Hari Martir IntelektualMemorial Martir Intelektual di Rayerbazar, DhakaNama resmibahasa Bengali: শহীদ বুদ্ধিজীবি দিবস Shaheed Buddhijibi Dibôsh'Dirayakan olehBangladeshMaknaperingatan eksekusi intelektual BengaliTanggal14 DesemberSelanjutnyaKesalahan ekspresi: Operator < tak terdugaFrekuensiannual Hari Martir Intelektual (bahasa Bengali: শহীদ বুদ্ধিজীবি দিবস Shaheed Buddhijibi Dibôsh) mengamati pada tanggal 1...

BraciglianoKomuneComune di BraciglianoLokasi Bracigliano di Provinsi SalernoNegara ItaliaWilayah CampaniaProvinsiSalerno (SA)Luas[1] • Total14,41 km2 (5,56 sq mi)Ketinggian[2]327 m (1,073 ft)Populasi (2016)[3] • Total5.439 • Kepadatan380/km2 (980/sq mi)Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos84082Kode area telepon081Situs webhttp://www.comune.bracigliano.sa.it B...

Sulawesi BaratProvinsiTranskripsi bahasa Mandar • Aksara Lontaraᨔᨘᨒᨓᨙᨔᨗ ᨅᨑDari atas ke bawah: Rumah adat Mandar, Pantai Dato Majene, Rumah adat Mamasa, tradisi Mangngaro di Mamasa, Pelabuhan Mamuju, Pantai Palippis, dan Tari Tondok BenderaLambangMotto: Mellete diatonganan(Mandar) Meniti pada kebenaranPetaNegara IndonesiaDasar hukum pendirianUU No. 26 Tahun 2004Hari jadi22 September 2004[1]Ibu kotaMamujuJumlah satuan pemerintahan Daftar Kabu...

العلاقات السويسرية المالية سويسرا مالي سويسرا مالي تعديل مصدري - تعديل العلاقات السويسرية المالية هي العلاقات الثنائية التي تجمع بين سويسرا ومالي.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة سويسرا مال...

Model to classify people in society This article is about the social class model. For the magnetism model, see magnetic moment. For telecommunications, see Gilbert–Elliot model. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be chall...

Carole Bayer SagerLahirCarole Bayer8 Maret 1947 (umur 77)Manhattan, New York City, Amerika SerikatTempat tinggalLos Angeles, CaliforniaPendidikanNew York UniversityPekerjaanPenulis lirik, penyanyi, penulis lagu, pelukis, penulisSuami/istriAndrew Sager (m. 1970–1978)Burt Bacharach (m. 1982–1991)Robert A. Daly (m. 1996)AnakCristopher Elton Bacharach Carole Bayer Sager (lahir 8 Maret 1947) adalah seorang penulis lirik, penyanyi, penulis lagu dan pelukis Amerika serta penulis best-selle...

Cave and archaeological site in Spain Cave of BacineteNative name Spanish: Cueva de BacineteLocationLos Barrios, SpainCoordinates36°11′53″N 5°33′25″W / 36.197997°N 5.556817°W / 36.197997; -5.556817 Spanish Cultural HeritageOfficial nameCave of BacineteTypeNon-movableCriteriaMonumentDesignated1985Reference no.RI-51-0011420 Location of Cave of Bacinete in Spain The Cave of Bacinete (Spanish: Cueva de Bacinete) is a cave located in Los Alcornocales Natura...

Halaman ini berisi artikel tentang wahana Mars India. Untuk pengorbit Mars lainnya, lihat Daftar misi ke Mars. Mars Orbiter MissionGambaran MOM saat mengorbit MarsJenis misiPengorbit MarsOperatorISROCOSPAR ID2013-060ASATCAT no.39370Situs webwww.isro.org/mars/home.aspxDurasi misi300 hari Properti wahanaBusI-1K[1]ProdusenISACMassa luncur1,337 kg (2,95 pon)[2]Massa kering500 kg (1.100 pon)[3]Massa muatan15 kg (33 pon)[4]Dimensi15...

Suicide bombing on 11 December 2016 inside a Coptic church in Cairo, Egypt Botroseya Church bombingChurch of SS. Peter and Paul in 2010LocationAbbassia, Cairo, EgyptDate11 December 2016 (2016-12-11) 10:00 (UTC+02:00)TargetCoptic ChristiansAttack typeBombingWeaponsSuicide vestDeaths189[1][2]Injured400+Perpetrators Islamic State - Sinai Province[3][4]AssailantMahmoud Shafiq Mohammed Mustafa[3] Martyrs of Botroseya ChurchMartyrsDied11 Decemb...

Parlemen Estonia RiigikoguJenisJenisUnikameral PimpinanPresidenJüri Ratas, EK sejak 18 Maret 2021 Wakil Presiden PertamaHanno Pevkur, RE sejak 8 Februari 2021 Wakil Presiden KeduaMartin Helme, EKRE sejak 18 Maret 2021 KomposisiAnggota101Partai & kursiPemerintah (34) R (34) Oposisi(67) EK (24) EKRE (19) Isamaa (12) SDE (9) Independen (3) PemilihanPemilihan terakhir1 March 2015Tempat bersidangKastil Toompea, TallinnSitus webwww.riigikog...

この記事には参考文献や外部リンクの一覧が含まれていますが、脚注による参照が不十分であるため、情報源が依然不明確です。 適切な位置に脚注を追加して、記事の信頼性向上にご協力ください。(2021年12月) 左からヘンリー・ラスボーン少佐、クララ・ハリス、メアリー・トッド・リンカーン、エイブラハム・リンカーン、ジョン・ウィルクス・ブース リンカー�...

Central Asian Persianate Turco-Mongol empire (1370–1507) Iran and Turanایران و توران1370–1507Motto: Persian:راستى رستىRāstī rustīIn rectitude lies salvationMap of the Timurid Empire at its greatest extent under Timur, vassals are not shownStatusEmirateCapital Samarkand (1370–1405) Herat (1405–1507) Common languages Persian (official, court language, high literature, lingua franca, administration)[1] Chagatai Turkic (dynastic, literature)[2&...
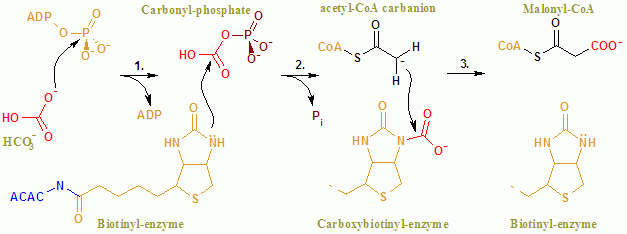
Acetyl-CoA carboxylase識別子EC番号 6.4.1.2CAS登録番号 9023-93-2 データベースIntEnz IntEnz viewBRENDA BRENDA entryExPASy NiceZyme viewKEGG KEGG entryMetaCyc metabolic pathwayPRIAM profilePDB構造 RCSB PDB PDBj PDBe PDBsum遺伝子オントロジー AmiGO / QuickGO 検索PMC articlesPubMed articlesNCBI proteinsテンプレートを表示 Acetyl-CoA carboxylase alpha識別子略号 ACACA他の略号 ACAC, ACC1, ACCAEntrez(英語版) 31HUGO 84OMIM 601557RefSeq NM_198839UniProt...
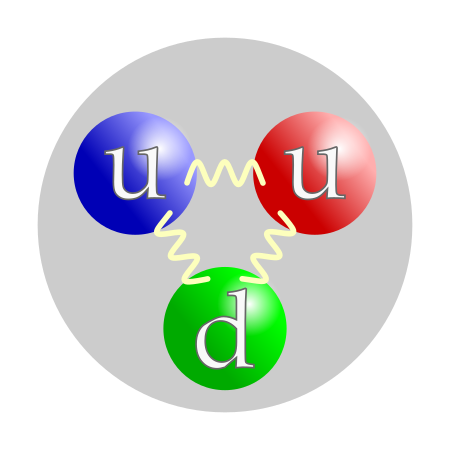
Particle smaller than an atom A composite particle proton is made of two up quarks and one down quark, which are elementary particles. In physics, a subatomic particle is a particle smaller than an atom.[1] According to the Standard Model of particle physics, a subatomic particle can be either a composite particle, which is composed of other particles (for example, a baryon, like a proton or a neutron, composed of three quarks; or a meson, composed of two quarks), or an elementary par...

Three transport rail systems in Las Vegas, Nevada Harry Reid International Airport Automated People MoversAutomated people mover at Harry ReidOverviewLocaleHarry Reid International Airport serving Las VegasStations4ServiceTypePeople moverServices3Operator(s)Clark County Department of AviationRolling stock16 Bombardier Innovia APM 100 vehiclesHistoryOpenedGreen Line: 1985Blue Line: 1998Red Line: 2012TechnicalLine length1.15 mi (1.85 km)Track length.27 mi (0.43 km) (Green Li...

Cet article concerne la Croix-Rouge française. Pour les autres Croix-Rouge, voir Liste des associations des Croix-Rouges et des Croissants-Rouges. Pour les articles homonymes, voir CRF. Croix-Rouge françaiseHistoireFondation 25 mai 1864CadreSigles CRF, CRfZone d'activité International (en)Type Association caritative, société nationale du Mouvement international de la Croix-Rouge et du Croissant-Rouge, organisation d'assistanceForme juridique Association reconnue d'utilité publique ...

イギリス海軍の「アーガス」。全通飛行甲板を採用した最初の飛行機母艦。イギリス海軍のクイーン・エリザベス級空母。アイランドを2つ設けた最初の航空母艦。 航空母艦(こうくうぼかん、英: aircraft carrier)は、航空機を多数搭載し、海上での航空基地の役割を果たす軍艦[1]。略称は空母(くうぼ)。 第一次世界大戦で登場し、その当時は飛行機母艦の名�...

Sir Richard Hoghton, 1st Baronet (28 September 1570 – 1630) was a politician who sat in the House of Commons between 1601 and 1611. Hoghton Tower. He was born the eldest son of Thomas Hoghton of Hoghton Tower, Lancashire by Anne, the daughter of Henry Keighley of Keighley, Yorkshire. Thomas was killed in family feud in 1589.[1] He was appointed High Sheriff of Lancashire for 1599 and was knighted in January 1600.[2] In 1601 he was elected Member of Parliament (MP) for Lanca...

Location of torri in Corsica[1] The Torrean civilization was a Bronze Age megalithic civilization that developed in Southern Corsica, mostly concentrated south of Ajaccio, during the second half of the second millennium BC. Part of a series on the History of Corsica Prehistory (c. 9000–566 BC) Arzachena culture Ozieri culture Torrean civilization Antiquity (566 BC – AD 455) Ancient tribes Aléria Lava Treasure Roman province of Sardinia and Corsica Medieval (455–1347) Battle of ...


