Честное равновесие
|
Read other articles:

SK Planet Co., Ltd. 에스케이 플래닛JenisAnak perusahaanIndustriInternetDidirikan1 Oktober 2011KantorpusatPangyo, Provinsi Gyeonggi, Korea SelatanTokohkunciSungWon Suh (CEO)ProdukE-CommerceOnline-to-OfflinePemasaran digitalPerdagangan seluler11st.co.krOK CashbagSyrupShopkickKaryawan2.283IndukSK TelecomSitus webwww.skplanet.com Artikel ini berisi konten yang ditulis dengan gaya sebuah iklan. Bantulah memperbaiki artikel ini dengan menghapus konten yang dianggap sebagai spam dan pranala l...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Halaman ini berisi artikel tentang deskripsi stereotipe. Untuk istilah Inggris angry young man, lihat Angry young man (disambiguasi). Berkas:愤青.jpgfenqing 愤青 Fenqing (Hanzi sederhana: 愤青; Hanzi tradisional: 憤青; Pinyin: Fènq...

Finnish boxer Sten SuvioSuvio in 1943Personal informationBorn25 November 1911Hannila, Viipuri Province, Imperial RussiaDied19 October 1988 (aged 76)Helsinki, FinlandHeight170 cm (5 ft 7 in)Weight65–68 kg (143–150 lb)SportSportBoxing Medal record Representing Finland Olympic Games 1936 Berlin Welterweight Sten Stepa Suvio (born Schuschin, 25 November 1911 – 19 October 1988) was a Finnish boxer who won the welterweight contest at the 1936 Summer Olympics. ...

Untuk pengertian lain, lihat Cenrana (disambiguasi). Sungai Cenranaᨔᨘᨂᨕᨗ ᨌᨛᨋᨊ Versi Indonesia ᨔᨒᨚ ᨌᨛᨋᨊ Versi BugisSalo Cenrana, Cenrana RiverEtimologidari Bahasa Bugis Salo berarti Sungai dan Cenrana merupakan nama daerahLokasiNegara IndonesiaProvinsiSulawesi SelatanKabupatenMaros & BoneCiri-ciri fisikHulu sungai - lokasiDesa Laiya, Kecamatan Cenrana, Kabupaten Maros Muara sungai - lokasiDesa Swadaya, Kecamatan Libureng,...

Hannah FergusonFerguson pada Februari 2015Lahir12 Oktober 1992 (umur 31)San Angelo, Texas, A.S.[1]PekerjaanModelTahun aktif2014–sekarangInformasi modelingTinggi177 m (580 ft 8+1⁄2 in)[2]Warna rambutPirang[2]Warna mataBiru[2]Manajer IMG Models (Worldwide) VIVA Model Management (Barcelona) Kim Dawson Agency (Dallas)[3] Hannah Emily Rose Ferguson[4] (lahir 12 Oktober 1992)[5] adalah seorang model asal Ameri...

Voce principale: Watford Football Club. Watford Football ClubStagione 2016-2017Sport calcio Squadra Watford Allenatore Walter Mazzarri Presidente Raffaele Riva Premier League17° FA CupQuarto turno Football League CupSecondo turno Maggiori presenzeCampionato: Heurelho Gomes (38)Totale: Troy Deeney (40) Miglior marcatoreCampionato: Troy Deeney (10)Totale: Troy Deeney (10) StadioVicarage Road Maggior numero di spettatori21,118 vs Manchester United (18 Settembre 2016) Minor numero di spett...

Bishop of London and saint (c. 620 – 664) For the Hong Kong government department, see Civil Engineering and Development Department. CeddBishop of LondonModern icon image of CeddInstalledc. 654Term ended664PredecessorMellitusSuccessorWinePersonal detailsBornc. 620Kingdom of NorthumbriaDied(664-10-26)26 October 664LastinghamSainthoodFeast day26 October, 7 January (Orthodox Church)Venerated inCatholic Church; Orthodox Church; AnglicanismTitle as SaintEvangelist of the Middle Angles and East S...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Dutch cyclist Maarten DucrotDucrot at the 2009 Tour de FrancePersonal informationFull nameMaarten DucrotBorn (1958-04-08) 8 April 1958 (age 66)Vlissingen, the NetherlandsTeam informationCurrent teamRetiredDisciplineRoadRoleRiderAmateur team1984Driessen–Transvemij–Colnago Professional teams1985–1988Kwantum–Decosol–Yoko1989Domex–Weinmann1990–1991TVM Major winsGrand Tours Tour de France 1 individual stage (1985) Combativity award (1985) Maarten Ducrot (born 8 April 1...

Northeastern Turkic language DukhaTsaatanтyъһа тыл Tuha tılNative toMongoliaRegionKhövsgöl ProvinceEthnicityDukhaNative speakers(undated figure of 500)[1]Language familyTurkic Common TurkicSiberian TurkicSouth SiberianSayan TurkicTaiga Sayan Turkic[1]DukhaLanguage codesISO 639-3None (mis)Glottologdukh1234ELPDukha Dukha or Dukhan is an endangered Turkic variety spoken by approximately five hundred people of the Dukhan (a.k.a. Tsaatan) people in the Tsagaan-Nuur c...
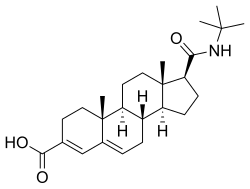
Chemical compound EpristerideClinical dataTrade namesAipuliete, ChuanliuOther namesONO-9302; SKF-105657; 17β-(tert-Butylcarbamoyl)androsta-3,5-diene-3-carboxylic acidRoutes ofadministrationBy mouth[1]Drug class5α-Reductase inhibitorATC codeNoneLegal statusLegal status In general: ℞ (Prescription only) Pharmacokinetic dataBioavailability93%[2]Elimination half-life26 hours[2]Identifiers IUPAC name (8S,9S,10R,13S,14S,17S)-17-(tert-butylcarbamoyl)-10,13-dimet...

Not to be confused with Reamker. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Riemke Bochum – news · newspapers · books · scholar · JSTOR (October 2023) (Learn how and when to remove this message) A view from the Tippelsberg Riemke is a major district of the city of Bochum, Ruhr area, North Rhine-Wes...

American tax forms Form 1042-S, 2016. Forms 1042, 1042-S and 1042-T are United States Internal Revenue Service tax forms dealing with payments to foreign persons, including nonresident aliens, foreign partnerships, foreign corporations, foreign estates, and foreign trusts.[1] Every withholding agent or intermediary, whether US or foreign, who has control, receipt, custody, disposal or payment of any fixed or determinable, annual or periodic US source income over foreign persons, must ...

Marisa PavanPavan pada 1965LahirMaria Luisa Pierangeli(1932-06-19)19 Juni 1932Cagliari, Sardinia, Kerajaan ItaliaMeninggal6 Desember 2023(2023-12-06) (umur 91)Gassin, PrancisPekerjaanAktrisTahun aktif1952–1992Suami/istriJean-Pierre Aumont (m. 1956; kematiannya 2001)Anak2 Marisa Pavan (lahir Maria Luisa Pierangeli; 19 Juni 1932 – 6 Desember 2023) adalah seorang pemeran kelahiran Italia. Ia mula-mula dikenal sebaga...

3rd president of Egypt from 1970 to 1981 His ExcellencyAnwar Sadatأنور الساداتSadat in 19803rd President of EgyptIn office15 October 1970 – 6 October 1981Acting: 28 September – 15 October 1970Prime Minister See list Mahmoud Fawzi (1970–1972) Aziz Sedki (1972–1973) Himself (1973–1974) Abdel Aziz Mohamed Hegazy (1974–1975) Mamdouh Salem (1975–1978) Mustafa Khalil (1978–1980) Himself (1980–1981) Vice President See list Hussein el-Shafei (1970–1973) Ali...

Halaman ini berisi artikel tentang Republik Federal Jerman pada tahun 1949 hingga 1990. Untuk Republik Federal Jerman setelah penyatuan kembali, lihat Jerman. Untuk Republik Federal Jerman pada 1919 hingga 1933, lihat Republik Weimar. Republik Federal JermanBundesrepublik Deutschland1949–1990 Bendera Lambang Semboyan: Einigkeit und Recht und Freiheit Persatuan dan keadilan dan kebebasanLagu kebangsaan: Ich hab' mich ergeben(Saya menyerah atas kelakuannya diri sendiri)(1949–1952)...

В Википедии есть статьи о других людях с такой фамилией, см. Алексеев; Алексеев, Александр; Алексеев, Александр Александрович. Александр Алексеев Позиция защитник Рост 193 см Вес 91 кг Хват левый Страна Россия Дата рождения 15 ноября 1999(1999-11-15) (24 года) Место рождения Санк...

الحقبة الحديثة المتأخرةمعلومات عامةالبداية القرن 18 التأثيراتفرع من العصر الحديث تفرع عنها التاريخ المعاصرالحرب العالمية الأولىالحرب العالمية الثانية الحقبة الحديثة المبكرة تعديل - تعديل مصدري - تعديل ويكي بيانات جزء من سلسلةتاريخ البشريةالحقبة البشرية ↑ ما قبل التاري�...

Pour les autres articles nationaux ou selon les autres juridictions, voir code civil. Code civil Données clés Autre(s) nom(s) Burgerlijk Wetboek (nl) Publication d'avant la numérotation des articles, avec pour chaque séance les discours des orateurs du gouvernement et les réponses. Présentation Langue(s) officielle(s) français, néerlandais Adoption et entrée en vigueur Adoption 21 mars 1804 Abrogation 1er novembre 2020 Lire en ligne http://www.droitbelge.be/codes.asp#civ Code civil ...

JB30 JM10 Stasiun Nishi-Funabashi西船橋駅Pintu masuk utara pada bulan September 2019Lokasi4-27-7 Nishifuna, Funabashi-shi, Chiba-kenJepangOperator JR East (manajer) Tokyo Metro Tōyō Rapid Railway Jalur JB Jalur Chūō-Sōbu JM Jalur Musashino JE Jalur Keiyo Jalur Tokyo Metro Tōzai Jalur Tōyō Rapid Railway Informasi lainKode stasiun JB30 (Chūō-Sōbu Line) JM10 (Musashino Line, Keiyō Line) T-23 (Tozai Line) TR01 (Toyo Rapid Railway Line) SejarahDibuka10 November 1958Operasi layanan ...








![{\displaystyle {\boldsymbol {\pi }}_{j}^{fair}(b_{j})={\frac {1}{2}}*[{\boldsymbol {\pi }}_{j}^{max}(b_{j})+{\boldsymbol {\pi }}_{j}^{min}(b_{j})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9940323775c89a6c4c52d280fe0bab74c53081f1)







![{\displaystyle U(a_{i},b_{j},c_{i})={\boldsymbol {\pi }}_{i}(a_{i},b_{j})+{\widetilde {f}}(b_{i},c_{i})[1+f(a_{i},b_{j})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8be3a246bd2c27271a978027d16c13544dbe86f5)
![{\displaystyle {\widetilde {f}}(b_{i},c_{i})[1+f(a_{i},b_{j})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5eb79e20217eb0d13e5013af68d7f33fe4834567)



