Уравнение Льенара

Уравнение Льенара — дифференциальное уравнение, часто использующееся в теории колебаний и динамических систем. Названо в честь французского физика А. Льенара.

Определение

Пусть $f$ и $g$ — две вещественные непрерывно-дифференцируемые функции, причём $g$ — нечётная функция, а $f$ — чётная. Тогда уравнение вида

{d^{2}x \over dt^{2}}+f(x){dx \over dt}+g(x)=0

называется уравнением Льенара.^[1]

Кроме того, уравнение Льенара можно^[2]^[3] свести к дифференциальному уравнению первого порядка, сделав замену $v={dx \over dt}$ . Тогда уравнение Льенара преобразуется в уравнение Абеля второго типа: $v{dv \over dx}+f(x)v+g(x)=0$

Примеры

Осциллятор Ван дер Поля ${d^{2}x \over dt^{2}}-\mu (1-x^{2}){dx \over dt}+x=0$ имеет вид уравнения Льенара при $\left\{{\begin{matrix}f(x)=\mu (1-x^{2})\\g(x)=x\end{matrix}}\right.$ .

Связанные определения

Система Льенара

Уравнение Льенара может быть преобразовано в систему дифференциальных уравнений.

Пусть

F(x):=\int _{0}^{x}f(\xi )d\xi

;

x_{1}:=x

;

x_{2}:={dx \over dt}+F(x)

Тогда система вида

{\begin{bmatrix}{\dot {x}}_{1}\\{\dot {x}}_{2}\end{bmatrix}}=\mathbf {h} (x_{1},x_{2}):={\begin{bmatrix}x_{2}-F(x_{1})\\-g(x_{1})\end{bmatrix}}

называется системой Льенара.

Теорема Льенара

Система Льенара имеет единственный и устойчивый предельный цикл около начала координат, если система удовлетворяет следующим трём свойствам:

$g(x)>0$ для всех $x>0$ ;
$\lim _{x\to \infty }F(x):=\lim _{x\to \infty }\int _{0}^{x}f(\xi )d\xi \ =\infty ;$
$F(x)$ имеет только один положительный корень при некотором значении параметра $p$ , причём

F(x)<0

при

0<x<p

F(x)>0

и монотонна при

x>p

См. также

Осциллятор

Примечания

↑ Liénard, A. (1928) "Etude des oscillations entretenues, " Revue générale de l'électricité 23, pp. 901—912 and 946—954.
↑ Liénard equation Архивная копия от 2 июня 2012 на Wayback Machine at eqworld.
↑ Abel equation of the second kind Архивная копия от 2 июня 2012 на Wayback Machine at eqworld.

Read other articles:

Sendang Tirto Kamandanu

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2018. Sendang Tirto Kamandanu adalah salah satu tempat wisata edukasi dan merupakan warisan budaya yang masih tetap dilestarikan yang berlokasi di Dusun Menang RT 03 RW 03 Desa Menang, Kecamatan Pagu, Kabupaten Kediri, Provinsi Jawa Timur. Sendang Tirto Kam...

Lawrence Ati-Zigi

Lawrence Ati-Zigi Ati-Zigi pada tahun 2017Informasi pribadiNama lengkap Lawrence Ati-Zigi[1]Tanggal lahir 29 November 1996 (umur 27)Tempat lahir Tamale, GhanaTinggi 188 m (616 ft 10 in)[2]Posisi bermain Penjaga gawangInformasi klubKlub saat ini St. GallenNomor 1Karier junior0000–2015 Red Bull GhanaKarier senior*Tahun Tim Tampil (Gol)2015–2017 Red Bull Salzburg 0 (0)2015–2017 → FC Liefering (dipinjam) 33 (0)2017–2020 Sochaux 23 (0)2020– St. Gall...

Ida Bagus Made

Ida Bagus MadeLahir1915Tebesaya, Ubud, Bali, Hindia BelandaMeninggal1999Ubud, Bali, IndonesiaKebangsaanIndonesiaDikenal atasPelukis Ida Bagus Made (lahir di Tebesaya, Peliatan, Ubud, Bali tahun 1915) alias Ida Bagus Made Poleng adalah seorang pelukis yang sering dianggap sebagai 'orang gila'.[1] Dalam kesehariannya, Ida Bagus Made tidak mengenakan pakaian, dia hanya mengenakan sarung yang dililitkan di pinggang. Ia yang tak pernah mengenyam pendidikan formal membuatnya, hanya bisa me...

List of Beowulf characters

Main articles: lists of figures in Germanic heroic legend and Beowulf This is a list of Beowulf characters. Beowulf is an Old English heroic epic poem. Its creation dates to between the 8th[1] and the 11th centuries, the only surviving manuscript dating to circa 1010.[2] At 3183 lines, it is notable for its length. It has reached national epic status in England (although its setting is Scandinavia, not the British Isles).[3] There are a great many characters in Beowul...

دوري أبطال أوروبا 2009–10

دوري أبطال أوروبا 2009–2010ملعب سانتياغو بيرنابيو المُستضيف للنهائي.تفاصيل المسابقةالتواريخ30 يونيو 2009 - 22 مايو 2010الفرق32 (دور المجموعات) (من 52 اتحاد)المراكز النهائيةالبطل إنتر ميلانالوصيف بايرن ميونخإحصائيات المسابقةالمباريات الملعوبة125الأهداف المسجلة318 (2٫54 لكل مب�...

Jordi Bolòs

Jordi BolòsBiographieNaissance 17 avril 1955 (68 ans)BarceloneNationalité espagnoleActivités Historien, professeur d'université, écrivainPère Oriol Bolos Capdevilla (en)Autres informationsA travaillé pour Université de LéridaSite web www.blogger.com/profile/13040949313306395284Œuvres principales Repertori d'Antropònims Catalans (d)modifier - modifier le code - modifier Wikidata Jordi Bolòs, né à Barcelone en 1955, est un historien médiéviste catalan, professeur de l'Unive...

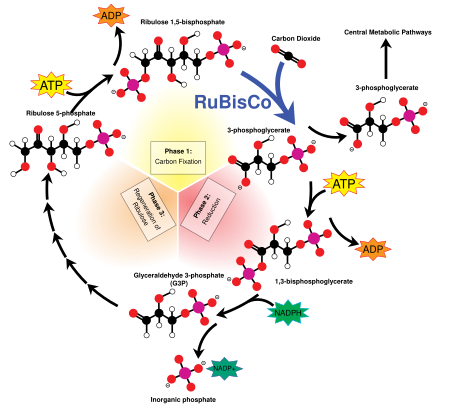
Ribulose 1,5-bisphosphate

Ribulose 1,5-bisphosphate The acid form of the RuBP anion Names IUPAC name 1,5-Di-O-phosphono-D-ribulose Other names Ribulose 1,5-diphosphate Identifiers CAS Number 2002-28-0 Y 3D model (JSmol) Interactive image ChEBI CHEBI:16710 Y ChemSpider 110238 Y KEGG C01182 PubChem CID 123658 UNII BR374X7NAH CompTox Dashboard (EPA) DTXSID30173837 InChI InChI=1S/C5H12O11P2/c6-3(1-15-17(9,10)11)5(8)4(7)2-16-18(12,13)14/h3,5-6,8H,1-2H2,(H2,9,10,11)(H2,12,13,14)/t3-,5-/m1/s1 YKey: ...

1960 United States presidential election in Virginia

Election in Virginia Main article: 1960 United States presidential election 1960 United States presidential election in Virginia ← 1956 November 8, 1960 1964 → Nominee Richard Nixon John F. Kennedy Party Republican Democratic Home state California Massachusetts Running mate Henry Cabot Lodge Jr. Lyndon B. Johnson Electoral vote 12 0 Popular vote 404,521 362,327 Percentage 52.44% 46.97% County and Independent City Results Nixon 40-50...

Belval, Vosges

Peta infrastruktur dan tata guna lahan di Komune Belval. = Kawasan perkotaan = Lahan subur = Padang rumput = Lahan pertanaman campuran = Hutan = Vegetasi perdu = Lahan basah = Anak sungaiBelval merupakan sebuah komune di departemen Vosges yang terletak pada sebelah timur laut Prancis. Lihat pula Komune di departemen Vosges Referensi INSEE lbsKomune di departemen Vosges Les Ableuvenettes Ahéville Aingeville Ainvelle Allarmont Ambacourt Ameuvelle...

Shaun Murphy (giocatore di snooker)

Shaun Murphy Nazionalità Inghilterra Biliardo Specialità Snooker Carriera Carriera professionistica Stagioni 1998-1999, 2001- Soprannome The Magician Ranking 7° (31 gennaio 2022) Miglior Ranking 3° (Maggio 2007-Maggio 2010, Aprile-Maggio 2016) Risultati nei tornei della Tripla Corona UK Championship V (2008) Masters V (2015) Campionato mondiale V (2005) Titoli Ranking 9 Titoli Non-Ranking 11 Century break 573 Miglior break 147 (6) Maggior vincita £250000Campionato mondiale 2005 St...

哥伦布 (密西西比州)

密西西比州哥伦布城市綽號：Possum Town哥伦布位于密西西比州的位置坐标：33°30′06″N 88°24′54″W / 33.501666666667°N 88.415°W / 33.501666666667; -88.415国家美國州密西西比州县朗兹县始建于1821年政府 • 市长罗伯特·史密斯 (民主党)面积 • 总计22.3 平方英里（57.8 平方公里） • 陸地21.4 平方英里（55.5 平方公里） • ...

哈萨克斯坦总统

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言，清晰概述条目所有重點。请在条目的讨论页讨论此问题。哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日（哈薩克蘇維埃社會主義共和國總統）哈萨克斯坦哈萨克斯坦政府...

Diálogo

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada. Busca fuentes: «Diálogo» – noticias · libros · académico · imágenesEste aviso fue puesto el 13 de marzo de 2015. Para otros usos de este término, véase Diálogo (desambiguación). Diálogo entre Goethe y Schiller. El diálogo es una manera de comunicación verbal o escrita en la que se comunican dos o más personas en un intercambio de información, alternándose el pap...

ديتكتيف بيكاتشو

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يناير 2018) ديتكتيف بيكاتشو Detective Pikachu الغلاف الفني الأوروبي للعبة المطور كرايتشرز إنك الناشر ذا بوكيمون كومباني الموزع نينتندو إي شوب المخرج ناوكي مياشيتا المبرمج �...

Campo di spezzamento

In algebra, un campo di spezzamento (o campo di riducibilità completa) di un polinomio p ( x ) {\displaystyle p(x)} , definito su un campo K {\displaystyle K} , è la più piccola estensione di K {\displaystyle K} che contiene tutte le radici di p ( x ) {\displaystyle p(x)} . Indice 1 Definizione 2 Costruzione 3 Unicità 4 Esempi 5 Bibliografia 6 Collegamenti esterni Definizione Sia K {\displaystyle K} un campo e p ( x ) {\displaystyle p(x)} un polinomio a coefficienti in K {\displaystyle K}...

Monterey Furniture

Mason Monterey A-frame chair from the Oregon Caves National Monument Chateau Monterey Furniture refers to several furniture lines made from 1930 to the mid-1940s in California. Uniquely western, the line derived its character from Spanish and Dutch Colonial styles, California Mission architecture and furnishings, ranch furnishings, and cowboy accoutrements such as might be found in a barn (lariats and branding irons). Mason Manufacturing Company, founded by Frank Mason and his son, George, ar...

Christian Munsee

Group of Lenape Indians For the Old Slavic tribe, see Moravians (tribe). For the Christian Indians in New England, see Praying Indians. The power of the Gospel: Zeisberger preaching to the Indians by Christian Schussele (1862) The Christian Munsee are a group of Lenape (also known as Delaware), an Indigenous people in the United States, that primarily speak Munsee and have converted to Christianity, following the teachings of Moravian missionaries. The Christian Munsee are also known as the M...

Iowa Alcoholic Beverages Division

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Iowa Alcoholic Beverages Division – news · newspapers · books · scholar · JSTOR (August 2019) (Learn how and when to remove this message) The Iowa Alcoholic Beverages Division is the alcoholic beverage control authority for the U.S. state of Iowa. Since March 8, 1934, it has regulated the traffic in, and m...

Chrysler PowerTech engine

This article is about the V6 and V8 engines. For other uses, see Chrysler PowerTech engine (disambiguation). Reciprocating internal combustion engine Powertech engineOverviewManufacturerDaimlerChrysler AG (1999–2007)Chrysler LLC (2007–2009)Chrysler Group LLC (2009-2013)Also calledNext Generation MagnumProduction1999–April 9, 2013[1]LayoutConfigurationNaturally aspirated 90° V6/V8Displacement3.7–4.7 L; 225.8–286.7 cu in (3,701–4,698 cc)Cylinder bore3.66...

قانون الأسرة في اليابان

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (ديسمبر 2016) قانون الأسرة في اليابانمعلومات عامةصنف فرعي من قانون الأسرةlaw of Japan (en) البداية 5 ديسمبر 1947 البلد اليابان الاختصاص اليابان الموضوع الرئيس كوسكي لغة العمل أو �...

PROFILPELAJAR.COM