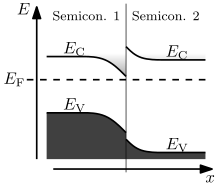
ะขัะตัะณะพะปัะฝะฐั ะบะฒะฐะฝัะพะฒะฐั ัะผะฐ
|
Read other articles:

Joint Meritorious Unit Award Pita untuk Angkatan Darat (atas)Pita untuk Angkatan Laut, Angkatan Udara, dan Astronot(bawah) Jenis Medali pita Persyaratan penerima Pasukan militer Status Masih berlaku Statistik Ditetapkan pada 4 Juni 1981; 42 tahun lalu (1981-06-04) Tingkatan Lebih tinggi Presidential Unit Citation Lebih rendah Valorous Unit Award StreamerBentuk Pita medali Joint Meritorious Unit Award atau Bintang Jasa Bersama adalah bintang penghargaan yang dianugerahkan kepad...

2020 American musical comedy drama streaming television series Julie and the PhantomsGenre Musical Comedy drama Created byDan Cross and David HogeBased onJulie e os Fantasmasby Paula Knudsen, Tiago Mello, and Fabio DanesiStarring Madison Reyes Charlie Gillespie Owen Patrick Joyner Jeremy Shada Jadah Marie Sacha Carlson Savannah May Music byDavid LawrenceCountry of originUnited StatesCanadaOriginal languageEnglishNo. of seasons1No. of episodes9ProductionExecutive producers Kenny Ortega Dan Cro...

The physiological basis for decompression theory and practice Scuba diver decompressing at a planned stop during ascent from a dive Not to be confused with Human physiology of underwater diving or Decompression sickness. The physiology of decompression is the aspect of physiology which is affected by exposure to large changes in ambient pressure. It involves a complex interaction of gas solubility, partial pressures and concentration gradients, diffusion, bulk transport and bubble mechanics ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ion Dincฤ โ news ยท newspapers ยท books ยท scholar ยท JSTOR (February 2013) (Learn how and when to remove this message) Ion Dincฤ Ion Dincฤ (November 3, 1928 โ January 9, 2007) was a Romanian communist politician and Army general who served as Deputy Prime Min...

Former political party in Luxembourg Politics of Luxembourg Constitution Law Monarchy Grand Duke (list) Henri Hereditary Grand Duke Prince Guillaume Executive Government: Frieden-Bettel Prime Minister: Luc Frieden Deputy Prime Minister: Xavier Bettel Legislature Chamber of Deputies President: Claude Wiseler Current members Council of State Elections Chamber circonscriptions Recent elections General: 201320182023 European: 201420192024 Communal: 200520112017 Political parties Administrative di...

Army service component command (ASCC)/theater army of the United States United States Army SouthUnited States Army South shoulder sleeve insigniaActive1986โpresentCountryUnited StatesBranchU.S. ArmyTypeArmy Service Component CommandRoleTheater ArmyPart ofUnited States Southern CommandGarrison/HQFort Sam Houston/Joint Base San AntonioMotto(s)Defense and FraternityEngagementsWorld War II Operation Just Cause Operation Uphold Democracy Operation Unified ResponseDecorationsMeritorious Unit...

Title for Mary, mother of Jesus For other uses, see Our Lady of Fรกtima (disambiguation). Our Lady of FรกtimaOur Lady of the Holy Rosary of FรกtimaThe canonically crowned image enshrined within the Chapel of the ApparitionsLocationFรกtima, PortugalDate13 May to 13 October 1917WitnessLรบcia dos Santos; Francisco and Jacinta MartoTypeMarian apparitionApproval13 October 1930: Josรฉ Alves Correia da Silva, Bishop of Leiria[1][2]25 April 1946: Pontifical decree of coronation by Pop...
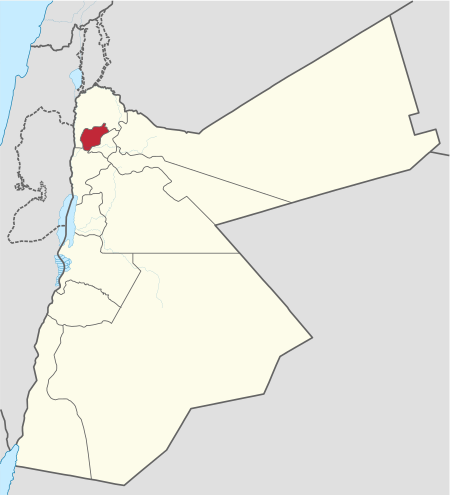
Governatorati della Giordania I governatorati della Giordania, o province (muhafazat, singolare: muhafazah) sono la suddivisione territoriale di primo livello del Paese e sono pari a 12. Lista Localizzazione Governatorato Nome in arabo Capoluogo Popolazione(2012) Superficie(kmยฒ) Governatorato di Ajlun ุนุฌููู Ajlun 146 900 420 Governatorato di Amman ุงูุนุงุตู ุฉ Amman 2 473 400 7 579 Governatorato di Aqaba ุงูุนูุจุฉ Aqaba 139 200 6 905 Governatorato di B...

็งๅ ่ไบยทๆฉๅพทๅบ็1958ๅนด10ๆ25ๆฅ ๏ผ65ๆญฒ๏ผ่ทๆฅญๆธธๆณณ่ฟๅจๅ ็งๅ ่ไบยทๆฉๅพท๏ผๅพท่ช๏ผKornelia Ender๏ผ1958ๅนด10ๆ25ๆฅโ๏ผ๏ผๅพทๅฝๅฅณๅญๆธธๆณณ่ฟๅจๅใๅฅนๆพไปฃ่กจไธๅพทๅๅ 1972ๅนดๅ1976ๅนดๅคๅญฃๅฅฅๆๅนๅ ่ฟๅจไผๆธธๆณณๆฏ่ต๏ผ่ทๅพๅๆ้็ๅๅๆ้ถ็ใ[1] ๅ่่ตๆ ^ Kornelia ENDER. International Olympic Committee. [2022-01-23]. ๏ผๅๅงๅ ๅฎนๅญๆกฃไบ2022-02-01๏ผ. ๆฅ่ฎบ็ผ ๅฅฅๆๅนๅ ่ฟๅจไผๆธธๆณณๆฏ๏ฟฝ...

ูุฐู ุงูู ูุงูุฉ ูุชูู ุฉ ุฅุฐ ุชุตู ุฅูููุง ู ูุงูุงุช ุฃุฎุฑู ููููุฉ ุฌุฏูุง. ูุถููุงุ ุณุงุนุฏ ุจุฅุถุงูุฉ ูุตูุฉ ุฅูููุง ูู ู ูุงูุงุช ู ุชุนููุฉ ุจูุง. (ููููู 2021) ูุซููุฉ ุฅุนูุงู ุงุณุชููุงู ุฌุงู ุงููุง ุญุตูุช ู ุณุชุนู ุฑุฉ ุฌุงู ุงููุง ุนูู ุงุณุชููุงููุง ู ู ุงูู ู ููุฉ ุงูู ุชุญุฏุฉ ูู 6 ุฃุบุณุทุณ 1962. ููุญุชูู ุจูุฐุง ุงูุชุงุฑูุฎ ูู ุฌุงู ุงููุง ุชุญุช ุงุณู ููู ุงูุงุณุชููุงูุ ููู ูู...

Protein-coding gene in the species Homo sapiens IFITM1IdentifiersAliasesIFITM1, 9-27, CD225, DSPA2a, IFI17, LEU13, interferon induced transmembrane protein 1External IDsOMIM: 604456; HomoloGene: 74501; GeneCards: IFITM1; OMA:IFITM1 - orthologsGene location (Human)Chr.Chromosome 11 (human)[1]Band11p15.5Start310,041 bp[1]End315,272 bp[1]RNA expression patternBgeeHumanMouse (ortholog)Top expressed inright ovarygranulocytecanal of the cervixleft uterine tubeleft ovaryright...

Castle in South Khorasan Province, Iran Babuk castleููุนู ุจุงุจฺูฉGeneral informationTypeCastleTown or cityBirjand CountyCountry IranBabuk castle (Persian: ููุนู ุจุงุจฺูฉ) is a historical castle located in Birjand County in South Khorasan Province; the longevity of this fortress dates back to the Qajar dynasty.[1][2] References ^ Encyclopaedia of the Iranian Architectural History. Cultural Heritage, Handicrafts and Tourism Organization of Iran. 15 February 2021. Arch...

Ethnikis Antistaseos Square, view from Maizonos Street. Ethnikis Antistaseos Square (Greek: ฮ ฮปฮฑฯฮตฮฏฮฑ ฮฮธฮฝฮนฮบฮฎฯ ฮฮฝฯฮนฯฯฮฌฯฮตฯฯ) is a central square in the city of Patras, Greece. Location and history The square is defined by the Aratou Street in the northeast, Maizonos Street in the southeast, Kolokotroni Street in the southwest and Riga Feraiou Street in the northwest. Originally the square was intended as a market, but it was planted with trees and became a public square k...

Serbian basketball player Nikola DragoviฤDragoviฤ with Spartak in March 2011.Free agentPositionPower forwardPersonal informationBorn (1987-12-20) December 20, 1987 (age 36)Titograd, SR Montenegro, SFR YugoslaviaNationalitySerbianListed height2.06 m (6 ft 9 in)Listed weight105 kg (231 lb)Career informationCollegeUCLA (2006โ2010)NBA draft2010: undraftedPlaying career2005โpresentCareer history2005โ2006Mega Ishrana2010โ2012Spartak Saint Petersburg2012โ201...

Nicol ร Leaรกin, Bishop of Kilmacduagh 1358โ1393. ร Leaรกin (O'Leane, Lane, Linnane) is associated with the Oranmore-Clarenbridge are of County Galway. ร Leaรกin was appointed 16 November 1358 and consecrated in 1360. He died before October 1393.[citation needed] See also Mauricius ร Leaรกin, Bishop of Kilmacduagh, 1254โ1284. Gregorius ร Leaรกin, Bishop of Kilmacduagh, 1394โ1397. Noel Lane (born 1954), retired Galway Gaelic Athletic Association (GAA) manager. Sylvie Linnan...

ูู ุนุงูู ุฃุฎุฑูุ ุทุงูุน ุจูุงูู (ุชูุถูุญ). ุจูููู ุนูู ุงูุฅุญุฏุงุซูุงุช 33ยฐ03โฒN 96ยฐ45โฒW / 33.05ยฐN 96.75ยฐW / 33.05; -96.75 [1] ุชุงุฑูุฎ ุงูุชุฃุณูุณ 1873 ุชูุณูู ุฅุฏุงุฑู ุงูุจูุฏ ุงูููุงูุงุช ุงูู ุชุญุฏุฉ[2][3] ุงูุชูุณูู ุงูุฃุนูู ู ูุงุทุนุฉ ูููููู ูุงุทุนุฉ ุฏููุชูู ุฎุตุงุฆุต ุฌุบุฑุงููุฉ ุงูู ุณุงุญุฉ 1...

American tennis player Hunter ReeseCountry (sports) United StatesResidenceKennesaw, Georgia, United StatesBorn (1993-01-11) January 11, 1993 (age 31)Atlanta, United StatesHeight1.80 m (5 ft 11 in)PlaysRight Handed (Double Handed Backhand)Prize money$283,148SinglesCareer record0โ0Career titles0DoublesCareer record18โ27Career titles0Highest rankingNo. 73 (27 June 2022)Current rankingNo. 182 (16 September 2024)Grand Slam doubles res...

Class of Taiwanese submarines ROCS Hai Lung (SS-793) Class overview NameChien Lung or Hai Lung BuildersWilton-Fijenoord Operators Republic of China Navy Succeeded byHai Kun class Built1982โ1986 In commission1987โpresent Planned2 Completed2 Active2 General characteristics TypeDiesel-electric attack submarine Displacement 2376 t (surfaced) 2660 t (submerged) Length66.9 m (219 ft 6 in) Beam8.4 m (27 ft 7 in) Draught6.7 m (22 ft 0 in) Pro...

Type of mammal For other uses, see Ibex (disambiguation). Male Alpine ibex An ibex (pl.: ibex, ibexes or ibices) is any of several species of wild goat (genus Capra), distinguished by the male's large recurved horns, which are transversely ridged in front. Ibex are found in Eurasia, North Africa and East Africa. Taxonomy The name ibex comes from Latin, borrowed from Iberian or Aquitanian, akin to Old Spanish bezerro, 'bull', modern Spanish becerro, 'yearling'. Ranging in height from 70 t...

Queen of Scotland from 1070 to 1093 This article is about the Scottish saint Margaret. For other saints named Margaret, see Saint Margaret (disambiguation). Saint MargaretSt Margaret from a medieval family tree, 13th centuryQueen consort of Alba (Scotland)Tenure1070 โ 13 November 1093Bornc. 1045Kingdom of HungaryDied(1093-11-16)16 November 1093 (aged 47โ48)Edinburgh Castle, Edinburgh, Kingdom of ScotlandBurialEl Escorial monastery, Madrid; formerly Dunfermline AbbeySpouseMalcolm III...
















































![{\displaystyle a_{n}\approx \left[{\frac {3\pi }{2}}\,\left(n-{\frac {1}{4}}\right)\right]^{2/3}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f9b6953905b1b92329d56373e64bce86c87fa26)


![{\displaystyle {\begin{aligned}&C_{n}^{2}{{\alpha }^{-1}}\int \limits _{-{{a}_{n}}}^{\infty }{d\xi }\mathrm {Ai} ^{2}\left(\xi \right)=\\&C_{n}^{2}{{\alpha }^{-1}}\left[\xi \mathrm {Ai} ^{2}\left(\xi \right)-{{\left(\mathrm {Ai} '\left(\xi \right)\right)}^{2}}\right]_{\xi =-{{a}_{n}}}^{\infty }=\\&C_{n}^{2}{{\alpha }^{-1}}{{\left(\mathrm {Ai} '\left(-{{a}_{n}}\right)\right)}^{2}}=1,\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b369734e7305ffa9cad46faf91ebc688827d4a66)




![{\displaystyle {\begin{aligned}&{{C}_{n}}{{C}_{m}}\int \limits _{0}^{\infty }{dx}\mathrm {Ai} \left(\alpha x-{{a}_{n}}\right)\mathrm {Ai} \left(\alpha x-{{a}_{m}}\right)=\\&{\frac {{{C}_{n}}{{C}_{m}}}{\alpha \left({{a}_{m}}-{{a}_{n}}\right)}}\left[\mathrm {Ai} '\left(\alpha x-{{a}_{n}}\right)\mathrm {Ai} \left(\alpha x-{{a}_{m}}\right)-\right.\\&\left.\mathrm {Ai} \left(\alpha x-{{a}_{n}}\right)\mathrm {Ai} '\left(\alpha x-{{a}_{m}}\right)\right]_{x=0}^{\infty }=0.\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53e571f7f9576d104c33c73536e2b8d8caa29a90)