–Δ–Β–Ψ―Ä–Β–Φ–Α –®―²–Β–Ι–Ϋ–Β―Ä–Α βÄî –ü–Ψ–Ϋ―¹–Β–Μ–Β
|
Read other articles:

Artikel ini perlu dikembangkan dari artikel terkait di Wikipedia bahasa Inggris. (Desember 2023) klik [tampil] untuk melihat petunjuk sebelum menerjemahkan. Lihat versi terjemahan mesin dari artikel bahasa Inggris. Terjemahan mesin Google adalah titik awal yang berguna untuk terjemahan, tapi penerjemah harus merevisi kesalahan yang diperlukan dan meyakinkan bahwa hasil terjemahan tersebut akurat, bukan hanya salin-tempel teks hasil terjemahan mesin ke dalam Wikipedia bahasa Indonesia. Ja...

Faces of Fear Paperback editionAuthorJohn SaulCountry United StatesLanguageEnglishGenreNovelPublisherBallantine BooksPublication dateAugust 12, 2008Media typePrint (hardcover & paperback)Pages324ISBN978-0-345-48705-6Preceded byThe Devil's Labyrinth Followed byHouse of Reckoning Faces of Fear is a thriller horror novel by John Saul, published by Ballantine Books on August 12, 2008. The novel follows the story of teenage Alison Shaw, who finds a shocking backg...

RantepaoKecamatanNegara IndonesiaProvinsiSulawesi SelatanKabupatenToraja UtaraPemerintahan βÄΔ CamatRonny Kala'suso, SEPopulasi βÄΔ Total26,811 (2.016)[1] jiwaKode Kemendagri73.26.01 Kode BPS7326090 Luas10,29 km¬≤Desa/kelurahan2 lembang9 kelurahan Jalan utama Rantepao pada tahun 1948 Rantepao (α®ëα®àα®ôα®³α®ïα®ö) adalah sebuah kecamatan di Kabupaten Toraja Utara, Sulawesi Selatan, Indonesia. Sebelum menjadi bagian dari Kabupaten Toraja Utara, Kecamatan Rantepa...

Neighbourhood in North 24 Parganas, West Bengal, IndiaRajarhatNeighbourhoodSkyline of RajarhatRajarhatLocation in West Bengal, IndiaShow map of West BengalRajarhatRajarhat (India)Show map of IndiaCoordinates: 22¬Α37βÄ≤0βÄ≥N 88¬Α31βÄ≤0βÄ≥E / 22.61667¬ΑN 88.51667¬ΑE / 22.61667; 88.51667Country IndiaStateWest BengalDistrictNorth 24 ParganasRegionGreater KolkataGovernment βÄΔ TypeMunicipal Corporation βÄΔ BodyBidhannagar Municipal CorporationArea&...

Ukrainian footballer Ivan Petriak Petriak in 2017Personal informationFull name Ivan Yevhenovych PetryakDate of birth (1994-03-13) 13 March 1994 (age 30)Place of birth Smila, UkraineHeight 1.71 m (5 ft 7 in)[1]Position(s) MidfielderTeam informationCurrent team Polissya Zhytomyr (on loan from Shakhtar Donetsk)Number 10Youth career2005βÄ™2007 Sports School #15 Kyiv2007βÄ™2008 Olympic Reserve School Kyiv2008βÄ™2010 Knyazha Shchaslyve2010βÄ™2011 RVUFK KyivSenior career*...

Cet article fournit diverses informations sur la psychanalyse en France. Chronologie 1900 : Parution en langue originale de L'InterprΟ©tation du rΟΣve (Die Traumdeutung) de Sigmund Freud. 1912 : correspondance d'Angelo Hesnard avec Freud. 1913 : RenΟ© Laforgue dΟ©couvre l'ouvrage de Freud sur les rΟΣves, il fait sa thΟ®se sur la schizophrΟ©nie du point de vue psychanalytique, puis fait une brΟ®ve analyse avec EugΟ©nie Sokolnicka. 1913 : Angelo Hesnard et Emmanuel RΟ©gis pu...

Les versions LX et LD de la Dodge Charger comporte les modΟ®les de 2006 Ο† 2023, soit la sixiΟ®me et la septiΟ®me gΟ©nΟ©ration de la Charger. Histoire La premiΟ®re Charger Ο©tait une voiture d'exposition de 1964 basΟ©e sur la Dodge Polara et Ο©quipΟ©e d'un moteur V8 Wedge 426. La premiΟ®re Charger de production, basΟ©e sur la Dodge Coronet, a Ο©tΟ© prΟ©sentΟ©e comme un modΟ®le de 1966. Il y avait plusieurs vΟ©hicules diffΟ©rents portant la plaque signalΟ©tique Charger, construites sur trois p...

Swedish politician Anna WallentheimAnna Wallentheim on 8 April 2016Member of the RiksdagIn office2014βÄ™2018ConstituencySkΟΞne Northern and Eastern Personal detailsBorn (1985-01-16) January 16, 1985 (age 39)Tynnered, Gothenburg, VΟΛstra GΟΕtaland, SwedenPolitical partySocial DemocratsOccupationTeacher Anna Wallentheim is a Swedish teacher and politician who serves in the Riksdag with the Social Democrats since 2014.[1][2][3][4] References ^ Anna Walle...

2017 U.S.-Saudi diplomatic meeting Riyadh Summit 2017King Salman, Presidents Trump and el-Sisi inaugurate the Global Center for Combating Extremism by touching an illuminated globe of the Earth.Host countrySaudi ArabiaDateMay 20, 2017 (2017-05-20) βÄ™ May 21, 2017 (2017-05-21)MottoTogether, We PrevailVenue(s)The Ritz-Carlton, RiyadhKing Abdulaziz International Conference CenterCities Riyadh, Saudi ArabiaParticipantsSee belowChairKing Salman of Saudi ArabiaWebsite...

For the early 20th century political party of similar name, see Independence Party (United States). For an ongoing minor party of similar name, see American Independent Party. Political party in United States Independence Party of America ChairmanFrank MacKayFoundedSeptember 23, 2007; 16 years ago (2007-09-23)DissolvedApril 2013 (2013-04)IdeologyNon-partisan democracyPopulismPolitics of United StatesPolitical partiesElections The Independence Party of America (...

Lower house of Indonesia's parliament House of Representatives Dewan Perwakilan Rakyat2019βÄ™2024TypeTypeLower house of the People's Consultative Assembly Term limitsNoneLeadershipSpeakerPuan Maharani (PDI-P) since 1 October 2019 Deputy SpeakerLodewijk Freidrich Paulus (Golkar) since 30 September 2021 Deputy SpeakerSufmi Dasco Ahmad (Gerindra) since 1 October 2019 Deputy SpeakerRachmad Gobel (NasDem) since 1 October 2019 Deputy SpeakerMuhaimin Iskandar (PKB) since 1 Octobe...

ΌÜΊßΊ·Όä Ί®ΌÜΊßΊΓ ΊßΌ³Ί§Ί≤ΊßΊΠΊ± ΊΣΊΘΊ≥Ί≥ ΊΙΊßΌÖ 1968 ΊßΌ³ΌÖΌ³ΊΙΊ® ΌÖΌ³ΊΙΊ® ΊΙΌÖΊ± Ί≠ΌÖΊßΊ·Όä ΊßΌ³Ί®Ό³Ί· ΊßΌ³Ί§Ί≤ΊßΊΠΊ± ΊßΌ³Ί·ΌàΊ±Όä ΊßΌ³Ί±ΊßΊ®ΊΖΊ© ΊßΌ³Ί§Ί≤ΊßΊΠΊ±ΌäΊ© ΊßΌ³ΌÖΊ≠ΊΣΊ±Ό¹Ί© ΊßΌ³ΊΘΌàΌ³Όâ ΊΣΊΙΊ·ΌäΌ³ ΌÖΊΒΊ·Ί±Όä - ΊΣΊΙΊ·ΌäΌ³ ΌÜΊßΊ·Όä Ί·ΌäΌÜΊßΌÖΌäΌÉΌäΊ© Ί®ΌÜΊßΊΓ ΊßΌ³Ί§Ί≤ΊßΊΠΊ± ΊΘΌà Ί·ΌäΌÜΊßΌÖΌäΌÉΌäΊ© Ί®ΌÜΊßΊΓ ΊßΌ³Ί§Ί≤ΊßΊΠΊ± Ό΅Όà ΌÜΊßΊ·Όç Ί§Ί≤ΊßΊΠΊ±Όä Ί≥ΊßΊ®Ό² Ό³ΌÉΊ±Ί© ΊßΌ³Ό²Ί·ΌÖ ΌÉΊßΌÜ ΌÖΌ²Ί±Ό΅ Ό¹Όä ΊßΌ³Ί§Ί≤ΊßΊΠΊ± ΊßΌ³ΊΙΊßΊΒΌÖΊ©. ΊΣΊΘΊ≥Ί≥ ΊßΌ³ΌÜΊßΊ·Όä Ί®οΩΫ...

American asset management and financial planning company Waddell & ReedCompany typeSubsidiaryFounded1937; 87 years ago (1937)Defunct2021FateAcquiredHeadquartersKansas City, Missouri, U.S.AUMUS$48 Billion (5th May 2021)[1]Websitewaddell.com Waddell & Reed Financial, Inc. was an American asset management and financial planning company founded in 1937 in Kansas City, Missouri. It was a publicly traded company from 1998 to 2021, and briefly had its headquarters i...
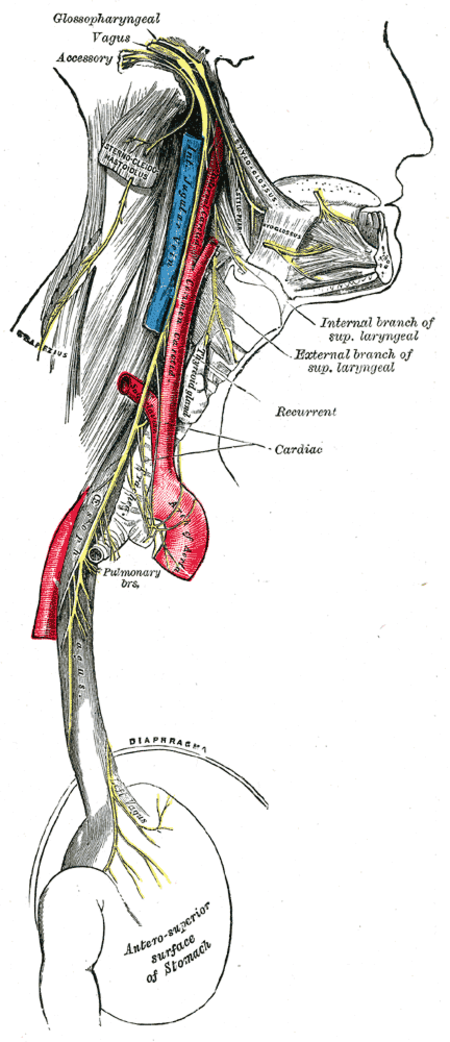
Saraf vagusDistribusi saraf glosofaringeal, vagus, dan aksesorius.RincianPersarafanLevator veli palatini, Salpingopharyngeus, Palatoglossus, Palatopharyngeus, Constrictor pharyngis superior, Constrictor pharyngis medius, Constrictor pharyngis inferior, viseraPengidentifikasiBahasa Latinnervus vagusMeSHD014630NeuroNames702TA98A14.2.01.153TA26332FMA5731Daftar istilah neuroanatomi[sunting di Wikidata] Saraf Kranial CN I βÄ™ Olfaktorius CN II βÄ™ Optikus CN III βÄ™ Okulomotor CN IV βÄ™ Trokle...

Seaside resort settlement in Devon, England This article is about the village. For the nearby nature reserve, see Dawlish Warren National Nature Reserve. Human settlement in EnglandDawlish WarrenDawlish WarrenLocation within DevonOS grid referenceSX979786Civil parishDawlishDistrictTeignbridgeShire countyDevonRegionSouth WestCountryEnglandSovereign stateUnited KingdomPost townDAWLISHPostcode districtEX7Dialling code01626PoliceDevon and CornwallFireDevon and Somers...

1991 American filmWizards of the Demon SwordVHS cover artDirected byFred Olen RayScreenplay byDan GoldenErnest FarinProduced byGrant Austin WaldmanFred Olen RayStarringRuss TamblynCinematographyGary GraverDistributed byTromaRelease date 1991 (1991) CountryUnited StatesLanguageEnglish Wizards of the Demon Sword is a 1991 film directed by Fred Olen Ray and starring Russ Tamblyn.[1][2] Premise Ulric's (Russ Tamblyn) daughter unites with warrior Thane (Blake Bahner) against e...

Expressway in Poland connecting Upper Silesia and Bielsko-Bia≈²a with Czechia Expressway S1Droga ekspresowa S1Route informationPart of E75 Maintained by GDDKiALength93.1 km (57.8 mi)132.81 km (82.52 mi) plannedMajor junctionsFrom A1 near Katowice International Airport in PyrzowiceMajor intersections 86 near Podwarpie 94 in DΡÖbrowa GΟ≥rnicza 79 in Mys≈²owice A4 near Mys≈²owice 86 near Tychy S52 near Bielsko-Bia≈²aTo D3 motorway, border with Slovakia LocationCountryPol...
Pour les articles homonymes, voir Hidalgo. Michel Hidalgo Michel Hidalgo en 1981. Biographie Nom Michel FranΟßois Hidalgo NationalitΟ© FranΟßaise Naissance 22 mars 1933 Leffrinckoucke (France) DΟ©cΟ®s 26 mars 2020 (Ο† 87 ans) Marseille 8e (France) Taille 1,68 m (5βÄ≤ 6βÄ≥) PΟ©riode pro. 1952 βÄ™ 1966 Poste Milieu de terrain puis entraΟ°neur Parcours junior AnnΟ©es Club 1946-1952 US Normande Parcours senior1 AnnΟ©esClub 0M.0(B.) {{parcours pro SΟ©lections en Ο©quipe nationale2 ...

Christian festival before Lent This article is about the Christian festival before Lent. Not to be confused with Traveling carnival or Carnival Cruise Line. For other uses, see Carnival (disambiguation). Carnival in Rome, c. 1650 Rio's Carnival is the largest in the world according to Guinness World Records.[1] Carnival or Shrovetide is a festive season that occurs at the close of the Christian pre-Lenten period,[2] consisting of Quinquagesima or Shrove Sunday, Shrove Mo...

2023 single by El Alfa and Prince RoyceLe Doy 20 MilSingle by El Alfa and Prince Roycefrom the album Llamada Perdida LanguageSpanishEnglish titleI give her 20 thousandReleasedFebruary 9, 2023GenreLatin urbanLength3:02LabelSony LatinSmiling Prince Music, Inc.El Alfa singles chronology Rulay & Pica Pollo (2023) Le Doy 20 Mil (2023) Doggy Doggy (2023) Prince Royce singles chronology Otra Vez(2022) Le Doy 20 Mil(2023) Me EnRD(2023) Music videoLe Doy 20 Mil on YouTube Le Doy 20 Mil is ...




