–°—Ö–Ķ–ľ–į –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź (Elgamal) ‚ÄĒ –ļ—Ä–ł–Ņ—ā–ĺ—Ā–ł—Ā—ā–Ķ–ľ–į —Ā –ĺ—ā–ļ—Ä—č—ā—č–ľ –ļ–Ľ—é—á–ĺ–ľ, –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–Ĺ–į—Ź –Ĺ–į —ā—Ä—É–ī–Ĺ–ĺ—Ā—ā–ł –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź –ī–ł—Ā–ļ—Ä–Ķ—ā–Ĺ—č—Ö –Ľ–ĺ–≥–į—Ä–ł—Ą–ľ–ĺ–≤ –≤ –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–ľ –Ņ–ĺ–Ľ–Ķ. –ö—Ä–ł–Ņ—ā–ĺ—Ā–ł—Ā—ā–Ķ–ľ–į –≤–ļ–Ľ—é—á–į–Ķ—ā –≤ —Ā–Ķ–Ī—Ź –į–Ľ–≥–ĺ—Ä–ł—ā–ľ —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź –ł –į–Ľ–≥–ĺ—Ä–ł—ā–ľ —Ü–ł—Ą—Ä–ĺ–≤–ĺ–Ļ –Ņ–ĺ–ī–Ņ–ł—Ā–ł. –°—Ö–Ķ–ľ–į –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź –Ľ–Ķ–∂–ł—ā –≤ –ĺ—Ā–Ĺ–ĺ–≤–Ķ –Ī—č–≤—ą–ł—Ö —Ā—ā–į–Ĺ–ī–į—Ä—ā–ĺ–≤ —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–Ĺ–ĺ–Ļ —Ü–ł—Ą—Ä–ĺ–≤–ĺ–Ļ –Ņ–ĺ–ī–Ņ–ł—Ā–ł –≤ –°–®–ź (DSA) –ł –†–ĺ—Ā—Ā–ł–ł (–ď–ě–°–Ę –† 34.10-94).
–°—Ö–Ķ–ľ–į –Ī—č–Ľ–į –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–Ķ–Ĺ–į –Ę–į—Ö–Ķ—Ä–ĺ–ľ –≠–Ľ—Ć-–ď–į–ľ–į–Ľ–Ķ–ľ –≤ 1985 –≥–ĺ–ī—É[1]. –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ć —Ä–į–∑—Ä–į–Ī–ĺ—ā–į–Ľ –ĺ–ī–ł–Ĺ –ł–∑ –≤–į—Ä–ł–į–Ĺ—ā–ĺ–≤ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–į –Ē–ł—Ą—Ą–ł-–•–Ķ–Ľ–Ľ–ľ–į–Ĺ–į. –ě–Ĺ —É—Ā–ĺ–≤–Ķ—Ä—ą–Ķ–Ĺ—Ā—ā–≤–ĺ–≤–į–Ľ —Ā–ł—Ā—ā–Ķ–ľ—É –Ē–ł—Ą—Ą–ł-–•–Ķ–Ľ–Ľ–ľ–į–Ĺ–į –ł –Ņ–ĺ–Ľ—É—á–ł–Ľ –ī–≤–į –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–į, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ľ–ł—Ā—Ć –ī–Ľ—Ź —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź –ł –ī–Ľ—Ź –ĺ–Ī–Ķ—Ā–Ņ–Ķ—á–Ķ–Ĺ–ł—Ź –į—É—ā–Ķ–Ĺ—ā–ł—Ą–ł–ļ–į—Ü–ł–ł. –í –ĺ—ā–Ľ–ł—á–ł–Ķ –ĺ—ā RSA, –į–Ľ–≥–ĺ—Ä–ł—ā–ľ –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź –Ĺ–Ķ –Ī—č–Ľ –∑–į–Ņ–į—ā–Ķ–Ĺ—ā–ĺ–≤–į–Ĺ –ł –Ņ–ĺ—ć—ā–ĺ–ľ—É —Ā—ā–į–Ľ –Ī–ĺ–Ľ–Ķ–Ķ –ī–Ķ—ą—Ď–≤–ĺ–Ļ –į–Ľ—Ć—ā–Ķ—Ä–Ĺ–į—ā–ł–≤–ĺ–Ļ, —ā–į–ļ –ļ–į–ļ –Ĺ–Ķ —ā—Ä–Ķ–Ī–ĺ–≤–į–Ľ–ĺ—Ā—Ć –ĺ–Ņ–Ľ–į—ā—č –≤–∑–Ĺ–ĺ—Ā–ĺ–≤ –∑–į –Ľ–ł—Ü–Ķ–Ĺ–∑–ł—é. –°—á–ł—ā–į–Ķ—ā—Ā—Ź, —á—ā–ĺ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ –Ņ–ĺ–Ņ–į–ī–į–Ķ—ā –Ņ–ĺ–ī –ī–Ķ–Ļ—Ā—ā–≤–ł–Ķ –Ņ–į—ā–Ķ–Ĺ—ā–į –Ē–ł—Ą—Ą–ł-–•–Ķ–Ľ–Ľ–ľ–į–Ĺ–į.
–ď–Ķ–Ĺ–Ķ—Ä–į—Ü–ł—Ź –ļ–Ľ—é—á–Ķ–Ļ
- –ď–Ķ–Ĺ–Ķ—Ä–ł—Ä—É–Ķ—ā—Ā—Ź —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā–ĺ–Ķ —á–ł—Ā–Ľ–ĺ
 .
.
- –í—č–Ī–ł—Ä–į–Ķ—ā—Ā—Ź —Ü–Ķ–Ľ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ
 ‚ÄĒ –Ņ–Ķ—Ä–≤–ĺ–ĺ–Ī—Ä–į–∑–Ĺ—č–Ļ –ļ–ĺ—Ä–Ķ–Ĺ—Ć
‚ÄĒ –Ņ–Ķ—Ä–≤–ĺ–ĺ–Ī—Ä–į–∑–Ĺ—č–Ļ –ļ–ĺ—Ä–Ķ–Ĺ—Ć  .
.
- –í—č–Ī–ł—Ä–į–Ķ—ā—Ā—Ź —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ķ —Ü–Ķ–Ľ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ
 —ā–į–ļ–ĺ–Ķ, —á—ā–ĺ
—ā–į–ļ–ĺ–Ķ, —á—ā–ĺ  .
.
- –í—č—á–ł—Ā–Ľ—Ź–Ķ—ā—Ā—Ź
 .
.
- –ě—ā–ļ—Ä—č—ā—č–ľ –ļ–Ľ—é—á–ĺ–ľ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź
 , –∑–į–ļ—Ä—č—ā—č–ľ –ļ–Ľ—é—á–ĺ–ľ ‚ÄĒ —á–ł—Ā–Ľ–ĺ
, –∑–į–ļ—Ä—č—ā—č–ľ –ļ–Ľ—é—á–ĺ–ľ ‚ÄĒ —á–ł—Ā–Ľ–ĺ  .
.
–†–į–Ī–ĺ—ā–į –≤ —Ä–Ķ–∂–ł–ľ–Ķ —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź
–®–ł—Ą—Ä–ĺ—Ā–ł—Ā—ā–Ķ–ľ–į –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ą–į–ļ—ā–ł—á–Ķ—Ā–ļ–ł –ĺ–ī–Ĺ–ł–ľ –ł–∑ —Ā–Ņ–ĺ—Ā–ĺ–Ī–ĺ–≤ –≤—č—Ä–į–Ī–ĺ—ā–ļ–ł –ĺ—ā–ļ—Ä—č—ā—č—Ö –ļ–Ľ—é—á–Ķ–Ļ –Ē–ł—Ą—Ą–ł ‚ÄĒ –•–Ķ–Ľ–Ľ–ľ–į–Ĺ–į.[–ł—Ā—ā–ĺ—á–Ĺ–ł–ļ –Ĺ–Ķ —É–ļ–į–∑–į–Ĺ 1107 –ī–Ĺ–Ķ–Ļ] –®–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł–Ķ –Ņ–ĺ —Ā—Ö–Ķ–ľ–Ķ –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź –Ĺ–Ķ —Ā–Ľ–Ķ–ī—É–Ķ—ā –Ņ—É—ā–į—ā—Ć —Ā –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–ĺ–ľ —Ü–ł—Ą—Ä–ĺ–≤–ĺ–Ļ –Ņ–ĺ–ī–Ņ–ł—Ā–ł –Ņ–ĺ —Ā—Ö–Ķ–ľ–Ķ –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź.
–®–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł–Ķ
–°–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ  –ī–ĺ–Ľ–∂–Ĺ–ĺ –Ī—č—ā—Ć –ľ–Ķ–Ĺ—Ć—ą–Ķ —á–ł—Ā–Ľ–į
–ī–ĺ–Ľ–∂–Ĺ–ĺ –Ī—č—ā—Ć –ľ–Ķ–Ĺ—Ć—ą–Ķ —á–ł—Ā–Ľ–į  . –°–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ —ą–ł—Ą—Ä—É–Ķ—ā—Ā—Ź —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ:
. –°–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ —ą–ł—Ą—Ä—É–Ķ—ā—Ā—Ź —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ:
- –í—č–Ī–ł—Ä–į–Ķ—ā—Ā—Ź —Ā–Ķ—Ā—Ā–ł–ĺ–Ĺ–Ĺ—č–Ļ –ļ–Ľ—é—á ‚ÄĒ —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ķ —Ü–Ķ–Ľ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ,
 —ā–į–ļ–ĺ–Ķ, —á—ā–ĺ
—ā–į–ļ–ĺ–Ķ, —á—ā–ĺ  .
.
- –í—č—á–ł—Ā–Ľ—Ź—é—ā—Ā—Ź —á–ł—Ā–Ľ–į
 –ł
–ł  .
.
- –ü–į—Ä–į —á–ł—Ā–Ķ–Ľ
 —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ą–ł—Ą—Ä–ĺ—ā–Ķ–ļ—Ā—ā–ĺ–ľ.
—Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ą–ł—Ą—Ä–ĺ—ā–Ķ–ļ—Ā—ā–ĺ–ľ.
–Ě–Ķ—ā—Ä—É–ī–Ĺ–ĺ –∑–į–ľ–Ķ—ā–ł—ā—Ć, —á—ā–ĺ –ī–Ľ–ł–Ĺ–į —ą–ł—Ą—Ä–ĺ—ā–Ķ–ļ—Ā—ā–į –≤ —Ā—Ö–Ķ–ľ–Ķ –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź –≤–ī–≤–ĺ–Ķ –Ī–ĺ–Ľ—Ć—ą–Ķ –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–≥–ĺ —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź  .
.
–†–į—Ā—ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł–Ķ
–ó–Ĺ–į—Ź –∑–į–ļ—Ä—č—ā—č–Ļ –ļ–Ľ—é—á  , –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–Ķ —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ –ľ–ĺ–∂–Ĺ–ĺ –≤—č—á–ł—Ā–Ľ–ł—ā—Ć –ł–∑ —ą–ł—Ą—Ä–ĺ—ā–Ķ–ļ—Ā—ā–į
, –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–Ķ —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ –ľ–ĺ–∂–Ĺ–ĺ –≤—č—á–ł—Ā–Ľ–ł—ā—Ć –ł–∑ —ą–ł—Ą—Ä–ĺ—ā–Ķ–ļ—Ā—ā–į  –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ:
–Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ:

–ü—Ä–ł —ć—ā–ĺ–ľ –Ĺ–Ķ—ā—Ä—É–ī–Ĺ–ĺ –Ņ—Ä–ĺ–≤–Ķ—Ä–ł—ā—Ć, —á—ā–ĺ

–ł –Ņ–ĺ—ć—ā–ĺ–ľ—É
- –Ě–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ —Ä–į–∑–ĺ–Ī—Ä–į—ā—Ć –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ (SVG (MathML –ľ–ĺ–∂–Ĺ–ĺ –≤–ļ–Ľ—é—á–ł—ā—Ć —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é –Ņ–Ľ–į–≥–ł–Ĺ–į –ī–Ľ—Ź –Ī—Ä–į—É–∑–Ķ—Ä–į): –Ě–Ķ–ī–ĺ–Ņ—É—Ā—ā–ł–ľ—č–Ļ –ĺ—ā–≤–Ķ—ā (¬ęMath extension cannot connect to Restbase.¬Ľ) –ĺ—ā —Ā–Ķ—Ä–≤–Ķ—Ä–į ¬ęhttp://localhost:6011/ru.wikipedia.org/v1/¬Ľ:): {\displaystyle b(a^x)^{-1} = (y^kM)g^{-xk}\equiv (g^{xk}M) g^{-xk}\equiv M \pmod{p}}
.
–Ē–Ľ—Ź –Ņ—Ä–į–ļ—ā–ł—á–Ķ—Ā–ļ–ł—Ö –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł–Ļ –Ī–ĺ–Ľ—Ć—ą–Ķ –Ņ–ĺ–ī—Ö–ĺ–ī–ł—ā —Ā–Ľ–Ķ–ī—É—é—Č–į—Ź —Ą–ĺ—Ä–ľ—É–Ľ–į:

–°—Ö–Ķ–ľ–į —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź
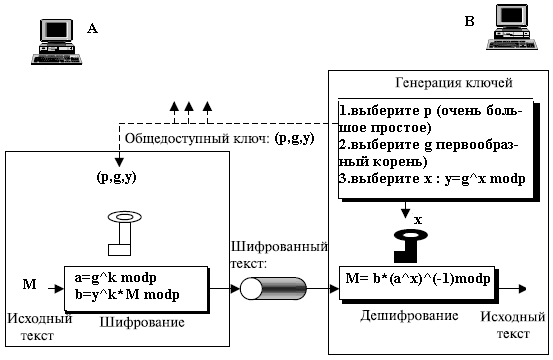
–ü—Ä–ł–ľ–Ķ—Ä
- –®–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł–Ķ
- –Ē–ĺ–Ņ—É—Ā—ā–ł–ľ, —á—ā–ĺ –Ĺ—É–∂–Ĺ–ĺ –∑–į—ą–ł—Ą—Ä–ĺ–≤–į—ā—Ć —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ
 .
.
- –ü—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–ľ –≥–Ķ–Ĺ–Ķ—Ä–į—Ü–ł—é –ļ–Ľ—é—á–Ķ–Ļ:
- –ü—É—Ā—ā—Ć
 . –í—č–Ī–Ķ—Ä–Ķ–ľ
. –í—č–Ī–Ķ—Ä–Ķ–ľ  ‚ÄĒ —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ķ —Ü–Ķ–Ľ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ
‚ÄĒ —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ķ —Ü–Ķ–Ľ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ  —ā–į–ļ–ĺ–Ķ, —á—ā–ĺ
—ā–į–ļ–ĺ–Ķ, —á—ā–ĺ  .
.
- –í—č—á–ł—Ā–Ľ–ł–ľ
 .
.
- –ė—ā–į–ļ, –ĺ—ā–ļ—Ä—č—ā—č–ľ –ļ–Ľ—é—á–ĺ–ľ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ā—Ä–ĺ–Ļ–ļ–į
 ,–į –∑–į–ļ—Ä—č—ā—č–ľ –ļ–Ľ—é—á–ĺ–ľ ‚ÄĒ —á–ł—Ā–Ľ–ĺ
,–į –∑–į–ļ—Ä—č—ā—č–ľ –ļ–Ľ—é—á–ĺ–ľ ‚ÄĒ —á–ł—Ā–Ľ–ĺ  .
.
- –í—č–Ī–ł—Ä–į–Ķ–ľ —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ķ —Ü–Ķ–Ľ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ
 —ā–į–ļ–ĺ–Ķ, —á—ā–ĺ 1 < k < (p ‚ąí 1). –ü—É—Ā—ā—Ć
—ā–į–ļ–ĺ–Ķ, —á—ā–ĺ 1 < k < (p ‚ąí 1). –ü—É—Ā—ā—Ć  .
.
- –í—č—á–ł—Ā–Ľ—Ź–Ķ–ľ —á–ł—Ā–Ľ–ĺ
 .
.
- –í—č—á–ł—Ā–Ľ—Ź–Ķ–ľ —á–ł—Ā–Ľ–ĺ
 .
.
- –ü–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–į—Ź –Ņ–į—Ä–į
 —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ą–ł—Ą—Ä–ĺ—ā–Ķ–ļ—Ā—ā–ĺ–ľ.
—Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ą–ł—Ą—Ä–ĺ—ā–Ķ–ļ—Ā—ā–ĺ–ľ.
- –†–į—Ā—ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł–Ķ
- –Ě–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –Ņ–ĺ–Ľ—É—á–ł—ā—Ć —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ
 –Ņ–ĺ –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ–ľ—É —ą–ł—Ą—Ä–ĺ—ā–Ķ–ļ—Ā—ā—É
–Ņ–ĺ –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ–ľ—É —ą–ł—Ą—Ä–ĺ—ā–Ķ–ļ—Ā—ā—É  –ł –∑–į–ļ—Ä—č—ā–ĺ–ľ—É –ļ–Ľ—é—á—É
–ł –∑–į–ļ—Ä—č—ā–ĺ–ľ—É –ļ–Ľ—é—á—É  .
.
- –í—č—á–ł—Ā–Ľ—Ź–Ķ–ľ M –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ:

- –ü–ĺ–Ľ—É—á–ł–Ľ–ł –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–Ķ —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ
 .
.
–Ę–į–ļ –ļ–į–ļ –≤ —Ā—Ö–Ķ–ľ—É –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź –≤–≤–ĺ–ī–ł—ā—Ā—Ź —Ā–Ľ—É—á–į–Ļ–Ĺ–į—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–į  ,—ā–ĺ —ą–ł—Ą—Ä –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź –ľ–ĺ–∂–Ĺ–ĺ –Ĺ–į–∑–≤–į—ā—Ć —ą–ł—Ą—Ä–ĺ–ľ –ľ–Ĺ–ĺ–≥–ĺ–∑–Ĺ–į—á–Ĺ–ĺ–Ļ –∑–į–ľ–Ķ–Ĺ—č. –ė–∑-–∑–į —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ—Ā—ā–ł –≤—č–Ī–ĺ—Ä–į —á–ł—Ā–Ľ–į
,—ā–ĺ —ą–ł—Ą—Ä –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź –ľ–ĺ–∂–Ĺ–ĺ –Ĺ–į–∑–≤–į—ā—Ć —ą–ł—Ą—Ä–ĺ–ľ –ľ–Ĺ–ĺ–≥–ĺ–∑–Ĺ–į—á–Ĺ–ĺ–Ļ –∑–į–ľ–Ķ–Ĺ—č. –ė–∑-–∑–į —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ—Ā—ā–ł –≤—č–Ī–ĺ—Ä–į —á–ł—Ā–Ľ–į  —ā–į–ļ—É—é —Ā—Ö–Ķ–ľ—É –Ķ—Č—Ď –Ĺ–į–∑—č–≤–į—é—ā —Ā—Ö–Ķ–ľ–ĺ–Ļ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–Ĺ–ĺ–≥–ĺ —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź. –í–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–Ĺ—č–Ļ —Ö–į—Ä–į–ļ—ā–Ķ—Ä —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ—Ä–Ķ–ł–ľ—É—Č–Ķ—Ā—ā–≤–ĺ–ľ –ī–Ľ—Ź —Ā—Ö–Ķ–ľ—č –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź, —ā–į–ļ –ļ–į–ļ —É —Ā—Ö–Ķ–ľ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–Ĺ–ĺ–≥–ĺ —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź –Ĺ–į–Ī–Ľ—é–ī–į–Ķ—ā—Ā—Ź –Ī–ĺ–Ľ—Ć—ą–į—Ź —Ā—ā–ĺ–Ļ–ļ–ĺ—Ā—ā—Ć –Ņ–ĺ —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—é —Ā–ĺ —Ā—Ö–Ķ–ľ–į–ľ–ł —Ā –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—č–ľ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–ľ —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź. –Ě–Ķ–ī–ĺ—Ā—ā–į—ā–ļ–ĺ–ľ —Ā—Ö–Ķ–ľ—č —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —É–ī–≤–ĺ–Ķ–Ĺ–ł–Ķ –ī–Ľ–ł–Ĺ—č –∑–į—ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–≥–ĺ —ā–Ķ–ļ—Ā—ā–į –Ņ–ĺ —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—é —Ā –Ĺ–į—á–į–Ľ—Ć–Ĺ—č–ľ —ā–Ķ–ļ—Ā—ā–ĺ–ľ. –Ē–Ľ—Ź —Ā—Ö–Ķ–ľ—č –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–Ĺ–ĺ–≥–ĺ —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź —Ā–į–ľ–ĺ —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ
—ā–į–ļ—É—é —Ā—Ö–Ķ–ľ—É –Ķ—Č—Ď –Ĺ–į–∑—č–≤–į—é—ā —Ā—Ö–Ķ–ľ–ĺ–Ļ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–Ĺ–ĺ–≥–ĺ —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź. –í–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–Ĺ—č–Ļ —Ö–į—Ä–į–ļ—ā–Ķ—Ä —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ—Ä–Ķ–ł–ľ—É—Č–Ķ—Ā—ā–≤–ĺ–ľ –ī–Ľ—Ź —Ā—Ö–Ķ–ľ—č –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź, —ā–į–ļ –ļ–į–ļ —É —Ā—Ö–Ķ–ľ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–Ĺ–ĺ–≥–ĺ —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź –Ĺ–į–Ī–Ľ—é–ī–į–Ķ—ā—Ā—Ź –Ī–ĺ–Ľ—Ć—ą–į—Ź —Ā—ā–ĺ–Ļ–ļ–ĺ—Ā—ā—Ć –Ņ–ĺ —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—é —Ā–ĺ —Ā—Ö–Ķ–ľ–į–ľ–ł —Ā –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—č–ľ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–ľ —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź. –Ě–Ķ–ī–ĺ—Ā—ā–į—ā–ļ–ĺ–ľ —Ā—Ö–Ķ–ľ—č —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —É–ī–≤–ĺ–Ķ–Ĺ–ł–Ķ –ī–Ľ–ł–Ĺ—č –∑–į—ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–≥–ĺ —ā–Ķ–ļ—Ā—ā–į –Ņ–ĺ —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—é —Ā –Ĺ–į—á–į–Ľ—Ć–Ĺ—č–ľ —ā–Ķ–ļ—Ā—ā–ĺ–ľ. –Ē–Ľ—Ź —Ā—Ö–Ķ–ľ—č –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–Ĺ–ĺ–≥–ĺ —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź —Ā–į–ľ–ĺ —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ  –ł –ļ–Ľ—é—á –Ĺ–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—ā —ą–ł—Ą—Ä–ĺ—ā–Ķ–ļ—Ā—ā –ĺ–ī–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ–ĺ. –í —Ā—Ö–Ķ–ľ–Ķ –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć —Ä–į–∑–Ľ–ł—á–Ĺ—č–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č
–ł –ļ–Ľ—é—á –Ĺ–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—ā —ą–ł—Ą—Ä–ĺ—ā–Ķ–ļ—Ā—ā –ĺ–ī–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ–ĺ. –í —Ā—Ö–Ķ–ľ–Ķ –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć —Ä–į–∑–Ľ–ł—á–Ĺ—č–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č  –ī–Ľ—Ź —ą–ł—Ą—Ä–ĺ–≤–ļ–ł —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ļ
–ī–Ľ—Ź —ą–ł—Ą—Ä–ĺ–≤–ļ–ł —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ļ  –ł
–ł  . –ē—Ā–Ľ–ł –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤—č–Ķ
. –ē—Ā–Ľ–ł –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤—č–Ķ  , —ā–ĺ –ī–Ľ—Ź —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł—Ö —ą–ł—Ą—Ä–ĺ—ā–Ķ–ļ—Ā—ā–ĺ–≤
, —ā–ĺ –ī–Ľ—Ź —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł—Ö —ą–ł—Ą—Ä–ĺ—ā–Ķ–ļ—Ā—ā–ĺ–≤  –ł
–ł  –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź–Ķ—ā—Ā—Ź —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ
–≤—č–Ņ–ĺ–Ľ–Ĺ—Ź–Ķ—ā—Ā—Ź —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ  . –ė–∑ —ć—ā–ĺ–≥–ĺ –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź –ľ–ĺ–∂–Ĺ–ĺ –Ľ–Ķ–≥–ļ–ĺ –≤—č—á–ł—Ā–Ľ–ł—ā—Ć
. –ė–∑ —ć—ā–ĺ–≥–ĺ –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź –ľ–ĺ–∂–Ĺ–ĺ –Ľ–Ķ–≥–ļ–ĺ –≤—č—á–ł—Ā–Ľ–ł—ā—Ć  , –Ķ—Ā–Ľ–ł –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ
, –Ķ—Ā–Ľ–ł –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ  .
.
–†–į–Ī–ĺ—ā–į –≤ —Ä–Ķ–∂–ł–ľ–Ķ –Ņ–ĺ–ī–Ņ–ł—Ā–ł
–¶–ł—Ą—Ä–ĺ–≤–į—Ź –Ņ–ĺ–ī–Ņ–ł—Ā—Ć —Ā–Ľ—É–∂–ł—ā –ī–Ľ—Ź —ā–ĺ–≥–ĺ —á—ā–ĺ–Ī—č –ľ–ĺ–∂–Ĺ–ĺ –Ī—č–Ľ–ĺ —É—Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ć –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –ī–į–Ĺ–Ĺ—č—Ö –ł —á—ā–ĺ–Ī—č —É—Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ć –Ņ–ĺ–ī–Ľ–ł–Ĺ–Ĺ–ĺ—Ā—ā—Ć –Ņ–ĺ–ī–Ņ–ł—Ā–į–≤—ą–Ķ–Ļ—Ā—Ź —Ā—ā–ĺ—Ä–ĺ–Ĺ—č. –ü–ĺ–Ľ—É—á–į—ā–Ķ–Ľ—Ć –Ņ–ĺ–ī–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–≥–ĺ —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź –ľ–ĺ–∂–Ķ—ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć —Ü–ł—Ą—Ä–ĺ–≤—É—é –Ņ–ĺ–ī–Ņ–ł—Ā—Ć –ī–Ľ—Ź –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–į —ā—Ä–Ķ—ā—Ć–Ķ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ —ā–ĺ–≥–ĺ, —á—ā–ĺ –Ņ–ĺ–ī–Ņ–ł—Ā—Ć –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ —Ā–ī–Ķ–Ľ–į–Ĺ–į –ĺ—ā–Ņ—Ä–į–≤–Ľ—Ź—é—Č–Ķ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ–ĺ–Ļ. –ü—Ä–ł —Ä–į–Ī–ĺ—ā–Ķ –≤ —Ä–Ķ–∂–ł–ľ–Ķ –Ņ–ĺ–ī–Ņ–ł—Ā–ł –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–į–≥–į–Ķ—ā—Ā—Ź –Ĺ–į–Ľ–ł—á–ł–Ķ —Ą–ł–ļ—Ā–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ļ —Ö–Ķ—ą-—Ą—É–Ĺ–ļ—Ü–ł–ł  , –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –Ľ–Ķ–∂–į—ā –≤ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–Ķ
, –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –Ľ–Ķ–∂–į—ā –≤ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–Ķ  .
.
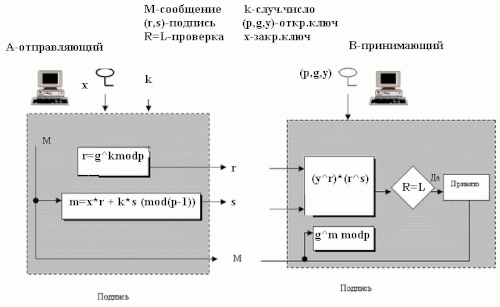 –¶–ł—Ą—Ä–ĺ–≤–į—Ź –Ņ–ĺ–ī–Ņ–ł—Ā—Ć –Ņ–ĺ —Ā—Ö–Ķ–ľ–Ķ –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź
–¶–ł—Ą—Ä–ĺ–≤–į—Ź –Ņ–ĺ–ī–Ņ–ł—Ā—Ć –Ņ–ĺ —Ā—Ö–Ķ–ľ–Ķ –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź
–ü–ĺ–ī–Ņ–ł—Ā—Ć —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ļ
–Ē–Ľ—Ź –Ņ–ĺ–ī–Ņ–ł—Ā–ł —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź  –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź—é—ā—Ā—Ź —Ā–Ľ–Ķ–ī—É—é—Č–ł–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł:
–≤—č–Ņ–ĺ–Ľ–Ĺ—Ź—é—ā—Ā—Ź —Ā–Ľ–Ķ–ī—É—é—Č–ł–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł:
- –í—č—á–ł—Ā–Ľ—Ź–Ķ—ā—Ā—Ź –ī–į–Ļ–ī–∂–Ķ—Ā—ā —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź
 :
:  (–•–Ķ—ą —Ą—É–Ĺ–ļ—Ü–ł—Ź –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ľ—é–Ī–į—Ź).
(–•–Ķ—ą —Ą—É–Ĺ–ļ—Ü–ł—Ź –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ľ—é–Ī–į—Ź).
- –í—č–Ī–ł—Ä–į–Ķ—ā—Ā—Ź —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ
 –≤–∑–į–ł–ľ–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā–ĺ–Ķ —Ā
–≤–∑–į–ł–ľ–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā–ĺ–Ķ —Ā  –ł –≤—č—á–ł—Ā–Ľ—Ź–Ķ—ā—Ā—Ź
–ł –≤—č—á–ł—Ā–Ľ—Ź–Ķ—ā—Ā—Ź 
- –í—č—á–ł—Ā–Ľ—Ź–Ķ—ā—Ā—Ź —á–ł—Ā–Ľ–ĺ
 , –≥–ī–Ķ
, –≥–ī–Ķ  —ć—ā–ĺ –ľ—É–Ľ—Ć—ā–ł–Ņ–Ľ–ł–ļ–į—ā–ł–≤–Ĺ–ĺ–Ķ –ĺ–Ī—Ä–į—ā–Ĺ–ĺ–Ķ
—ć—ā–ĺ –ľ—É–Ľ—Ć—ā–ł–Ņ–Ľ–ł–ļ–į—ā–ł–≤–Ĺ–ĺ–Ķ –ĺ–Ī—Ä–į—ā–Ĺ–ĺ–Ķ  –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é
–Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é  , –ļ–ĺ—ā–ĺ—Ä–ĺ–Ķ –ľ–ĺ–∂–Ĺ–ĺ –Ĺ–į–Ļ—ā–ł, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é —Ä–į—Ā—ą–ł—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–į –ē–≤–ļ–Ľ–ł–ī–į.
, –ļ–ĺ—ā–ĺ—Ä–ĺ–Ķ –ľ–ĺ–∂–Ĺ–ĺ –Ĺ–į–Ļ—ā–ł, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é —Ä–į—Ā—ą–ł—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–į –ē–≤–ļ–Ľ–ł–ī–į.
- –ü–ĺ–ī–Ņ–ł—Ā—Ć—é —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź
 —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–į—Ä–į
—Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–į—Ä–į  .
.
–ü—Ä–ĺ–≤–Ķ—Ä–ļ–į –Ņ–ĺ–ī–Ņ–ł—Ā–ł
–ó–Ĺ–į—Ź –ĺ—ā–ļ—Ä—č—ā—č–Ļ –ļ–Ľ—é—á  , –Ņ–ĺ–ī–Ņ–ł—Ā—Ć
, –Ņ–ĺ–ī–Ņ–ł—Ā—Ć  —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź
—Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź  –Ņ—Ä–ĺ–≤–Ķ—Ä—Ź–Ķ—ā—Ā—Ź —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ:
–Ņ—Ä–ĺ–≤–Ķ—Ä—Ź–Ķ—ā—Ā—Ź —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ:
- –ü—Ä–ĺ–≤–Ķ—Ä—Ź–Ķ—ā—Ā—Ź –≤—č–Ņ–ĺ–Ľ–Ĺ–ł–ľ–ĺ—Ā—ā—Ć —É—Ā–Ľ–ĺ–≤–ł–Ļ:
 –ł
–ł  .
.
- –ē—Ā–Ľ–ł —Ö–ĺ—ā—Ź –Ī—č –ĺ–ī–Ĺ–ĺ –ł–∑ –Ĺ–ł—Ö –Ĺ–Ķ –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź–Ķ—ā—Ā—Ź, —ā–ĺ –Ņ–ĺ–ī–Ņ–ł—Ā—Ć —Ā—á–ł—ā–į–Ķ—ā—Ā—Ź –Ĺ–Ķ–≤–Ķ—Ä–Ĺ–ĺ–Ļ.
- –í—č—á–ł—Ā–Ľ—Ź–Ķ—ā—Ā—Ź –ī–į–Ļ–ī–∂–Ķ—Ā—ā

- –ü–ĺ–ī–Ņ–ł—Ā—Ć —Ā—á–ł—ā–į–Ķ—ā—Ā—Ź –≤–Ķ—Ä–Ĺ–ĺ–Ļ, –Ķ—Ā–Ľ–ł –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź–Ķ—ā—Ā—Ź —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ:

–ö–ĺ—Ä—Ä–Ķ–ļ—ā–Ĺ–ĺ—Ā—ā—Ć –Ņ—Ä–ĺ–≤–Ķ—Ä–ļ–ł
–†–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ–ľ—č–Ļ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ –ļ–ĺ—Ä—Ä–Ķ–ļ—ā–Ķ–Ĺ –≤ —ā–ĺ–ľ —Ā–ľ—č—Ā–Ľ–Ķ, —á—ā–ĺ –Ņ–ĺ–ī–Ņ–ł—Ā—Ć, –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ–į—Ź –Ņ–ĺ —É–ļ–į–∑–į–Ĺ–Ĺ—č–ľ –≤—č—ą–Ķ –Ņ—Ä–į–≤–ł–Ľ–į–ľ, –Ī—É–ī–Ķ—ā –Ņ—Ä–ł–Ĺ—Ź—ā–į –Ņ—Ä–ł –Ķ—Ď –Ņ—Ä–ĺ–≤–Ķ—Ä–ļ–Ķ.
–ü—Ä–Ķ–ĺ–Ī—Ä–į–∑—É—Ź –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ  , –ł–ľ–Ķ–Ķ–ľ
, –ł–ľ–Ķ–Ķ–ľ

–Ē–į–Ľ–Ķ–Ķ, –ł–∑ –ú–į–Ľ–ĺ–Ļ —ā–Ķ–ĺ—Ä–Ķ–ľ—č –§–Ķ—Ä–ľ–į —Ā–Ľ–Ķ–ī—É–Ķ—ā, —á—ā–ĺ

–ü—Ä–ł–ľ–Ķ—Ä
- –ü–ĺ–ī–Ņ–ł—Ā—Ć —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź.
- –Ē–ĺ–Ņ—É—Ā—ā–ł–ľ, —á—ā–ĺ –Ĺ—É–∂–Ĺ–ĺ –Ņ–ĺ–ī–Ņ–ł—Ā–į—ā—Ć —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ
 .
.
- –ü—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–ľ –≥–Ķ–Ĺ–Ķ—Ä–į—Ü–ł—é –ļ–Ľ—é—á–Ķ–Ļ:
- –ü—É—Ā—ā—Ć

 –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–Ķ, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ł–∑–≤–Ķ—Ā—ā–Ĺ—č –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–ľ—É —Ā–ĺ–ĺ–Ī—Č–Ķ—Ā—ā–≤—É.
–Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–Ķ, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ł–∑–≤–Ķ—Ā—ā–Ĺ—č –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–ľ—É —Ā–ĺ–ĺ–Ī—Č–Ķ—Ā—ā–≤—É.
- –°–Ķ–ļ—Ä–Ķ—ā–Ĺ—č–Ļ –ļ–Ľ—é—á
 ‚ÄĒ —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ķ —Ü–Ķ–Ľ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ
‚ÄĒ —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ķ —Ü–Ķ–Ľ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ  —ā–į–ļ–ĺ–Ķ, —á—ā–ĺ
—ā–į–ļ–ĺ–Ķ, —á—ā–ĺ  .
.
- –í—č—á–ł—Ā–Ľ—Ź–Ķ–ľ –ĺ—ā–ļ—Ä—č—ā—č–Ļ –ļ–Ľ—é—á
 :
:  .
.
- –ė—ā–į–ļ, –ĺ—ā–ļ—Ä—č—ā—č–ľ –ļ–Ľ—é—á–ĺ–ľ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ā—Ä–ĺ–Ļ–ļ–į
 .
.
- –Ę–Ķ–Ņ–Ķ—Ä—Ć –≤—č—á–ł—Ā–Ľ—Ź–Ķ–ľ —Ö–Ķ—ą-—Ą—É–Ĺ–ļ—Ü–ł—é:
 .
.
- –í—č–Ī–Ķ—Ä–Ķ–ľ —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ķ —Ü–Ķ–Ľ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ
 —ā–į–ļ–ĺ–Ķ, —á—ā–ĺ –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź–Ķ—ā—Ā—Ź —É—Ā–Ľ–ĺ–≤–ł–Ķ
—ā–į–ļ–ĺ–Ķ, —á—ā–ĺ –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź–Ķ—ā—Ā—Ź —É—Ā–Ľ–ĺ–≤–ł–Ķ  . –ü—É—Ā—ā—Ć
. –ü—É—Ā—ā—Ć  .
.
- –í—č—á–ł—Ā–Ľ—Ź–Ķ–ľ
 .
.
- –Ě–į—Ö–ĺ–ī–ł–ľ
 . –Ę–į–ļ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā, —ā–į–ļ –ļ–į–ļ –Ě–ě–Ē
. –Ę–į–ļ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā, —ā–į–ļ –ļ–į–ļ –Ě–ě–Ē . –ē–≥–ĺ –ľ–ĺ–∂–Ĺ–ĺ –Ĺ–į–Ļ—ā–ł —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é —Ä–į—Ā—ą–ł—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–į –ē–≤–ļ–Ľ–ł–ī–į. –ü–ĺ–Ľ—É—á–ł–ľ
. –ē–≥–ĺ –ľ–ĺ–∂–Ĺ–ĺ –Ĺ–į–Ļ—ā–ł —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é —Ä–į—Ā—ą–ł—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–į –ē–≤–ļ–Ľ–ł–ī–į. –ü–ĺ–Ľ—É—á–ł–ľ 
- –Ě–į—Ö–ĺ–ī–ł–ľ —á–ł—Ā–Ľ–ĺ
 . –ü–ĺ–Ľ—É—á–ł–ľ
. –ü–ĺ–Ľ—É—á–ł–ľ  , —ā–į–ļ –ļ–į–ļ
, —ā–į–ļ –ļ–į–ļ 
- –ė—ā–į–ļ, –ľ—č –Ņ–ĺ–ī–Ņ–ł—Ā–į–Ľ–ł —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ:
 .
.
- –ü—Ä–ĺ–≤–Ķ—Ä–ļ–į –Ņ–ĺ–ī–Ľ–ł–Ĺ–Ĺ–ĺ—Ā—ā–ł –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź.
- –í—č—á–ł—Ā–Ľ—Ź–Ķ–ľ —Ö–Ķ—ą-—Ą—É–Ĺ–ļ—Ü–ł—é:
 .
.
- –ü—Ä–ĺ–≤–Ķ—Ä—Ź–Ķ–ľ —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ
 .
.
- –í—č—á–ł—Ā–Ľ–ł–ľ –Ľ–Ķ–≤—É—é —á–į—Ā—ā—Ć –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é 23:
 .
.
- –í—č—á–ł—Ā–Ľ–ł–ľ –Ņ—Ä–į–≤—É—é —á–į—Ā—ā—Ć –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é 23:
 .
.
- –Ę–į–ļ –ļ–į–ļ –Ņ—Ä–į–≤–į—Ź –ł –Ľ–Ķ–≤–į—Ź —á–į—Ā—ā–ł —Ä–į–≤–Ĺ—č, —ā–ĺ —ć—ā–ĺ –ĺ–∑–Ĺ–į—á–į–Ķ—ā —á—ā–ĺ –Ņ–ĺ–ī–Ņ–ł—Ā—Ć –≤–Ķ—Ä–Ĺ–į.
- –ď–Ľ–į–≤–Ĺ—č–ľ –Ņ—Ä–Ķ–ł–ľ—É—Č–Ķ—Ā—ā–≤–ĺ–ľ —Ā—Ö–Ķ–ľ—č —Ü–ł—Ą—Ä–ĺ–≤–ĺ–Ļ –Ņ–ĺ–ī–Ņ–ł—Ā–ł –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć –≤—č—Ä–į–Ī–į—ā—č–≤–į—ā—Ć —Ü–ł—Ą—Ä–ĺ–≤—č–Ķ –Ņ–ĺ–ī–Ņ–ł—Ā–ł –ī–Ľ—Ź –Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ —á–ł—Ā–Ľ–į —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ļ —Ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ–ľ —ā–ĺ–Ľ—Ć–ļ–ĺ –ĺ–ī–Ĺ–ĺ–≥–ĺ —Ā–Ķ–ļ—Ä–Ķ—ā–Ĺ–ĺ–≥–ĺ –ļ–Ľ—é—á–į. –ß—ā–ĺ–Ī—č –∑–Ľ–ĺ—É–ľ—č—ą–Ľ–Ķ–Ĺ–Ĺ–ł–ļ—É –Ņ–ĺ–ī–ī–Ķ–Ľ–į—ā—Ć –Ņ–ĺ–ī–Ņ–ł—Ā—Ć, –Ķ–ľ—É –Ĺ—É–∂–Ĺ–ĺ —Ä–Ķ—ą–ł—ā—Ć —Ā–Ľ–ĺ–∂–Ĺ—č–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–Ķ –∑–į–ī–į—á–ł —Ā –Ĺ–į—Ö–ĺ–∂–ī–Ķ–Ĺ–ł–Ķ–ľ –Ľ–ĺ–≥–į—Ä–ł—Ą–ľ–į –≤ –Ņ–ĺ–Ľ–Ķ
 . –°–Ľ–Ķ–ī—É–Ķ—ā —Ā–ī–Ķ–Ľ–į—ā—Ć –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –ļ–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–Ķ–≤:
. –°–Ľ–Ķ–ī—É–Ķ—ā —Ā–ī–Ķ–Ľ–į—ā—Ć –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –ļ–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–Ķ–≤:
- –°–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ
 –ī–ĺ–Ľ–∂–Ĺ–ĺ —Ā—Ä–į–∑—É –Ņ–ĺ—Ā–Ľ–Ķ –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź –Ņ–ĺ–ī–Ņ–ł—Ā–ł —É–Ĺ–ł—á—ā–ĺ–∂–į—ā—Ć—Ā—Ź, —ā–į–ļ –ļ–į–ļ –Ķ—Ā–Ľ–ł –∑–Ľ–ĺ—É–ľ—č—ą–Ľ–Ķ–Ĺ–Ĺ–ł–ļ –∑–Ĺ–į–Ķ—ā —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ
–ī–ĺ–Ľ–∂–Ĺ–ĺ —Ā—Ä–į–∑—É –Ņ–ĺ—Ā–Ľ–Ķ –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź –Ņ–ĺ–ī–Ņ–ł—Ā–ł —É–Ĺ–ł—á—ā–ĺ–∂–į—ā—Ć—Ā—Ź, —ā–į–ļ –ļ–į–ļ –Ķ—Ā–Ľ–ł –∑–Ľ–ĺ—É–ľ—č—ą–Ľ–Ķ–Ĺ–Ĺ–ł–ļ –∑–Ĺ–į–Ķ—ā —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ  –ł —Ā–į–ľ—É –Ņ–ĺ–ī–Ņ–ł—Ā—Ć, —ā–ĺ –ĺ–Ĺ –Ľ–Ķ–≥–ļ–ĺ –ľ–ĺ–∂–Ķ—ā –Ĺ–į–Ļ—ā–ł —Ā–Ķ–ļ—Ä–Ķ—ā–Ĺ—č–Ļ –ļ–Ľ—é—á –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ:
–ł —Ā–į–ľ—É –Ņ–ĺ–ī–Ņ–ł—Ā—Ć, —ā–ĺ –ĺ–Ĺ –Ľ–Ķ–≥–ļ–ĺ –ľ–ĺ–∂–Ķ—ā –Ĺ–į–Ļ—ā–ł —Ā–Ķ–ļ—Ä–Ķ—ā–Ĺ—č–Ļ –ļ–Ľ—é—á –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ:  –ł –Ņ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—Ć—é –Ņ–ĺ–ī–ī–Ķ–Ľ–į—ā—Ć –Ņ–ĺ–ī–Ņ–ł—Ā—Ć.
–ł –Ņ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—Ć—é –Ņ–ĺ–ī–ī–Ķ–Ľ–į—ā—Ć –Ņ–ĺ–ī–Ņ–ł—Ā—Ć.
–ß–ł—Ā–Ľ–ĺ  –ī–ĺ–Ľ–∂–Ĺ–ĺ –Ī—č—ā—Ć —Ā–Ľ—É—á–į–Ļ–Ĺ—č–ľ –ł –Ĺ–Ķ –ī–ĺ–Ľ–∂–Ĺ–ĺ –ī—É–Ī–Ľ–ł—Ä–ĺ–≤–į—ā—Ć—Ā—Ź –ī–Ľ—Ź —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö –Ņ–ĺ–ī–Ņ–ł—Ā–Ķ–Ļ, –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ—č—Ö –Ņ—Ä–ł –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤–ĺ–ľ –∑–Ĺ–į—á–Ķ–Ĺ–ł–ł —Ā–Ķ–ļ—Ä–Ķ—ā–Ĺ–ĺ–≥–ĺ –ļ–Ľ—é—á–į.
–ī–ĺ–Ľ–∂–Ĺ–ĺ –Ī—č—ā—Ć —Ā–Ľ—É—á–į–Ļ–Ĺ—č–ľ –ł –Ĺ–Ķ –ī–ĺ–Ľ–∂–Ĺ–ĺ –ī—É–Ī–Ľ–ł—Ä–ĺ–≤–į—ā—Ć—Ā—Ź –ī–Ľ—Ź —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö –Ņ–ĺ–ī–Ņ–ł—Ā–Ķ–Ļ, –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ—č—Ö –Ņ—Ä–ł –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤–ĺ–ľ –∑–Ĺ–į—á–Ķ–Ĺ–ł–ł —Ā–Ķ–ļ—Ä–Ķ—ā–Ĺ–ĺ–≥–ĺ –ļ–Ľ—é—á–į.
- –ė—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ —Ā–≤–Ķ—Ä—ā–ļ–ł
 –ĺ–Ī—ä—Ź—Ā–Ĺ—Ź–Ķ—ā—Ā—Ź —ā–Ķ–ľ, —á—ā–ĺ —ć—ā–ĺ –∑–į—Č–ł—Č–į–Ķ—ā –Ņ–ĺ–ī–Ņ–ł—Ā—Ć –ĺ—ā –Ņ–Ķ—Ä–Ķ–Ī–ĺ—Ä–į —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ļ –Ņ–ĺ –ł–∑–≤–Ķ—Ā—ā–Ĺ—č–ľ –∑–Ľ–ĺ—É–ľ—č—ą–Ľ–Ķ–Ĺ–Ĺ–ł–ļ—É –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź–ľ –Ņ–ĺ–ī–Ņ–ł—Ā–ł. –ü—Ä–ł–ľ–Ķ—Ä: –Ķ—Ā–Ľ–ł –≤—č–Ī—Ä–į—ā—Ć —Ā–Ľ—É—á–į–Ļ–Ĺ—č–Ķ —á–ł—Ā–Ľ–į
–ĺ–Ī—ä—Ź—Ā–Ĺ—Ź–Ķ—ā—Ā—Ź —ā–Ķ–ľ, —á—ā–ĺ —ć—ā–ĺ –∑–į—Č–ł—Č–į–Ķ—ā –Ņ–ĺ–ī–Ņ–ł—Ā—Ć –ĺ—ā –Ņ–Ķ—Ä–Ķ–Ī–ĺ—Ä–į —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ļ –Ņ–ĺ –ł–∑–≤–Ķ—Ā—ā–Ĺ—č–ľ –∑–Ľ–ĺ—É–ľ—č—ą–Ľ–Ķ–Ĺ–Ĺ–ł–ļ—É –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź–ľ –Ņ–ĺ–ī–Ņ–ł—Ā–ł. –ü—Ä–ł–ľ–Ķ—Ä: –Ķ—Ā–Ľ–ł –≤—č–Ī—Ä–į—ā—Ć —Ā–Ľ—É—á–į–Ļ–Ĺ—č–Ķ —á–ł—Ā–Ľ–į  ,—É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź—é—Č–ł–Ķ —É—Ā–Ľ–ĺ–≤–ł—Ź–ľ
,—É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź—é—Č–ł–Ķ —É—Ā–Ľ–ĺ–≤–ł—Ź–ľ  , –Ě–ě–Ē(j, p-1)=1 –ł –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–ł—ā—Ć —á—ā–ĺ
, –Ě–ě–Ē(j, p-1)=1 –ł –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–ł—ā—Ć —á—ā–ĺ



—ā–ĺ –Ľ–Ķ–≥–ļ–ĺ —É–ī–ĺ—Ā—ā–ĺ–≤–Ķ—Ä–ł—ā—Ć—Ā—Ź –≤ —ā–ĺ–ľ, —á—ā–ĺ –Ņ–į—Ä–į  —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≤–Ķ—Ä–Ĺ–ĺ–Ļ —Ü–ł—Ą—Ä–ĺ–≤–ĺ–Ļ –Ņ–ĺ–ī–Ņ–ł—Ā—Ć—é –ī–Ľ—Ź —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź
—Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≤–Ķ—Ä–Ĺ–ĺ–Ļ —Ü–ł—Ą—Ä–ĺ–≤–ĺ–Ļ –Ņ–ĺ–ī–Ņ–ł—Ā—Ć—é –ī–Ľ—Ź —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź  .
.
- –¶–ł—Ą—Ä–ĺ–≤–į—Ź –Ņ–ĺ–ī–Ņ–ł—Ā—Ć –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź —Ā—ā–į–Ľ–į –Ņ—Ä–ł–ľ–Ķ—Ä–ĺ–ľ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –ī—Ä—É–≥–ł—Ö –Ņ–ĺ–ī–Ņ–ł—Ā–Ķ–Ļ, —Ā—Ö–ĺ–∂–ł—Ö –Ņ–ĺ —Ā–≤–ĺ–ł–ľ —Ā–≤–ĺ–Ļ—Ā—ā–≤–į–ľ. –í –ł—Ö –ĺ—Ā–Ĺ–ĺ–≤–Ķ –Ľ–Ķ–∂–ł—ā –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł–Ķ —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź:
 , –≤ –ļ–ĺ—ā–ĺ—Ä–ĺ–ľ —ā—Ä–ĺ–Ļ–ļ–į
, –≤ –ļ–ĺ—ā–ĺ—Ä–ĺ–ľ —ā—Ä–ĺ–Ļ–ļ–į  –Ņ—Ä–ł–Ĺ–ł–ľ–į–Ķ—ā –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –ĺ–ī–Ĺ–ĺ–Ļ –ł–∑ –Ņ–Ķ—Ä–Ķ—Ā—ā–į–Ĺ–ĺ–≤–ĺ–ļ ¬Īr, ¬Īs –ł ¬Īm –Ņ—Ä–ł –ļ–į–ļ–ĺ–ľ-—ā–ĺ –≤—č–Ī–ĺ—Ä–Ķ –∑–Ĺ–į–ļ–ĺ–≤. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –ł—Ā—Ö–ĺ–ī–Ĺ–į—Ź —Ā—Ö–Ķ–ľ–į –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź –Ņ–ĺ–Ľ—É—á–į–Ķ—ā—Ā—Ź –Ņ—Ä–ł
–Ņ—Ä–ł–Ĺ–ł–ľ–į–Ķ—ā –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –ĺ–ī–Ĺ–ĺ–Ļ –ł–∑ –Ņ–Ķ—Ä–Ķ—Ā—ā–į–Ĺ–ĺ–≤–ĺ–ļ ¬Īr, ¬Īs –ł ¬Īm –Ņ—Ä–ł –ļ–į–ļ–ĺ–ľ-—ā–ĺ –≤—č–Ī–ĺ—Ä–Ķ –∑–Ĺ–į–ļ–ĺ–≤. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –ł—Ā—Ö–ĺ–ī–Ĺ–į—Ź —Ā—Ö–Ķ–ľ–į –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź –Ņ–ĺ–Ľ—É—á–į–Ķ—ā—Ā—Ź –Ņ—Ä–ł  ,
,  ,
,  .–Ě–į —ā–į–ļ–ĺ–ľ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –Ņ–ĺ–ī–Ņ–ł—Ā–ł —Ā–ī–Ķ–Ľ–į–Ĺ—č —Ā—ā–į–Ĺ–ī–į—Ä—ā—č —Ü–ł—Ą—Ä–ĺ–≤–ĺ–Ļ –Ņ–ĺ–ī–Ņ–ł—Ā–ł –°–®–ź –ł –†–ĺ—Ā—Ā–ł–ł. –í –į–ľ–Ķ—Ä–ł–ļ–į–Ĺ—Ā–ļ–ĺ–ľ —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ķ DSS (Digital Signature Standard), –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź
.–Ě–į —ā–į–ļ–ĺ–ľ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –Ņ–ĺ–ī–Ņ–ł—Ā–ł —Ā–ī–Ķ–Ľ–į–Ĺ—č —Ā—ā–į–Ĺ–ī–į—Ä—ā—č —Ü–ł—Ą—Ä–ĺ–≤–ĺ–Ļ –Ņ–ĺ–ī–Ņ–ł—Ā–ł –°–®–ź –ł –†–ĺ—Ā—Ā–ł–ł. –í –į–ľ–Ķ—Ä–ł–ļ–į–Ĺ—Ā–ļ–ĺ–ľ —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ķ DSS (Digital Signature Standard), –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź  ,
,  ,
,  , –į –≤ –†–ĺ—Ā—Ā–ł–Ļ—Ā–ļ–ĺ–ľ —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ķ:
, –į –≤ –†–ĺ—Ā—Ā–ł–Ļ—Ā–ļ–ĺ–ľ —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ķ:  ,
,  ,
,  .
.
- –ē—Č—Ď –ĺ–ī–Ĺ–ł–ľ –ł–∑ –Ņ—Ä–Ķ–ł–ľ—É—Č–Ķ—Ā—ā–≤ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć —É–ľ–Ķ–Ĺ—Ć—ą–Ķ–Ĺ–ł—Ź –ī–Ľ–ł–Ĺ—č –Ņ–ĺ–ī–Ņ–ł—Ā–ł —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é –∑–į–ľ–Ķ–Ĺ—č –Ņ–į—Ä—č —á–ł—Ā–Ķ–Ľ
 –Ĺ–į –Ņ–į—Ä—É —á–ł—Ā–Ķ–Ľ
–Ĺ–į –Ņ–į—Ä—É —á–ł—Ā–Ķ–Ľ  ), –≥–ī–Ķ
), –≥–ī–Ķ  —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ļ–į–ļ–ł–ľ-—ā–ĺ –Ņ—Ä–ĺ—Ā—ā—č–ľ –ī–Ķ–Ľ–ł—ā–Ķ–Ľ–Ķ–ľ —á–ł—Ā–Ľ–į
—Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ļ–į–ļ–ł–ľ-—ā–ĺ –Ņ—Ä–ĺ—Ā—ā—č–ľ –ī–Ķ–Ľ–ł—ā–Ķ–Ľ–Ķ–ľ —á–ł—Ā–Ľ–į  . –ü—Ä–ł —ć—ā–ĺ–ľ —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –ī–Ľ—Ź –Ņ—Ä–ĺ–≤–Ķ—Ä–ļ–ł –Ņ–ĺ–ī–Ņ–ł—Ā–ł –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é
. –ü—Ä–ł —ć—ā–ĺ–ľ —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –ī–Ľ—Ź –Ņ—Ä–ĺ–≤–Ķ—Ä–ļ–ł –Ņ–ĺ–ī–Ņ–ł—Ā–ł –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é  –Ĺ—É–∂–Ĺ–ĺ –∑–į–ľ–Ķ–Ĺ–ł—ā—Ć –Ĺ–į –Ĺ–ĺ–≤–ĺ–Ķ —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é
–Ĺ—É–∂–Ĺ–ĺ –∑–į–ľ–Ķ–Ĺ–ł—ā—Ć –Ĺ–į –Ĺ–ĺ–≤–ĺ–Ķ —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é  :
:  . –Ę–į–ļ —Ā–ī–Ķ–Ľ–į–Ĺ–ĺ –≤ –į–ľ–Ķ—Ä–ł–ļ–į–Ĺ—Ā–ļ–ĺ–ľ —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ķ DSS (Digital Signature Standard).
. –Ę–į–ļ —Ā–ī–Ķ–Ľ–į–Ĺ–ĺ –≤ –į–ľ–Ķ—Ä–ł–ļ–į–Ĺ—Ā–ļ–ĺ–ľ —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ķ DSS (Digital Signature Standard).
–ö—Ä–ł–Ņ—ā–ĺ—Ā—ā–ĺ–Ļ–ļ–ĺ—Ā—ā—Ć –ł –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–ł
–í –Ĺ–į—Ā—ā–ĺ—Ź—Č–Ķ–Ķ –≤—Ä–Ķ–ľ—Ź –ļ—Ä–ł–Ņ—ā–ĺ—Ā–ł—Ā—ā–Ķ–ľ—č —Ā –ĺ—ā–ļ—Ä—č—ā—č–ľ –ļ–Ľ—é—á–ĺ–ľ —Ā—á–ł—ā–į—é—ā—Ā—Ź –Ĺ–į–ł–Ī–ĺ–Ľ–Ķ–Ķ –Ņ–Ķ—Ä—Ā–Ņ–Ķ–ļ—ā–ł–≤–Ĺ—č–ľ–ł. –ö –Ĺ–ł–ľ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā—Ā—Ź –ł —Ā—Ö–Ķ–ľ–į –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź, –ļ—Ä–ł–Ņ—ā–ĺ—Ā—ā–ĺ–Ļ–ļ–ĺ—Ā—ā—Ć –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–į –Ĺ–į –≤—č—á–ł—Ā–Ľ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —Ā–Ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ—č –ī–ł—Ā–ļ—Ä–Ķ—ā–Ĺ–ĺ–≥–ĺ –Ľ–ĺ–≥–į—Ä–ł—Ą–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź, –≥–ī–Ķ –Ņ–ĺ –ł–∑–≤–Ķ—Ā—ā–Ĺ—č–ľ p, g –ł y —ā—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź –≤—č—á–ł—Ā–Ľ–ł—ā—Ć x, —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź—é—Č–ł–Ļ —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—é:

–ď–ě–°–Ę –†34.10-1994, –Ņ—Ä–ł–Ĺ—Ź—ā—č–Ļ –≤ 1994 –≥–ĺ–ī—É –≤ –†–ĺ—Ā—Ā–ł–Ļ—Ā–ļ–ĺ–Ļ –§–Ķ–ī–Ķ—Ä–į—Ü–ł–ł, —Ä–Ķ–≥–Ľ–į–ľ–Ķ–Ĺ—ā–ł—Ä–ĺ–≤–į–≤—ą–ł–Ļ –Ņ—Ä–ĺ—Ü–Ķ–ī—É—Ä—č —Ą–ĺ—Ä–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –ł –Ņ—Ä–ĺ–≤–Ķ—Ä–ļ–ł —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–Ĺ–ĺ–Ļ —Ü–ł—Ą—Ä–ĺ–≤–ĺ–Ļ –Ņ–ĺ–ī–Ņ–ł—Ā–ł, –Ī—č–Ľ –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ –Ĺ–į —Ā—Ö–Ķ–ľ–Ķ –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź. –° 2001 –≥–ĺ–ī–į –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –Ĺ–ĺ–≤—č–Ļ –ď–ě–°–Ę –† 34.10-2001, –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—Č–ł–Ļ –į—Ä–ł—Ą–ľ–Ķ—ā–ł–ļ—É —ć–Ľ–Ľ–ł–Ņ—ā–ł—á–Ķ—Ā–ļ–ł—Ö –ļ—Ä–ł–≤—č—Ö, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—č—Ö –Ĺ–į–ī –Ņ—Ä–ĺ—Ā—ā—č–ľ–ł –Ņ–ĺ–Ľ—Ź–ľ–ł –ď–į–Ľ—É–į. –°—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –Ī–ĺ–Ľ—Ć—ą–ĺ–Ķ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–ĺ–≤, –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–Ĺ—č—Ö –Ĺ–į —Ā—Ö–Ķ–ľ–Ķ –≠–Ľ—Ć-–ď–į–ľ–į–Ľ—Ź: —ć—ā–ĺ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ—č DSA, ECDSA, KCDSA, —Ā—Ö–Ķ–ľ–į –®–Ĺ–ĺ—Ä—Ä–į.
–°—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č—Ö –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–ĺ–≤:
| –ź–Ľ–≥–ĺ—Ä–ł—ā–ľ
|
–ö–Ľ—é—á
|
–Ě–į–∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ
|
–ö—Ä–ł–Ņ—ā–ĺ—Ā—ā–ĺ–Ļ–ļ–ĺ—Ā—ā—Ć, MIPS
|
–ü—Ä–ł–ľ–Ķ—á–į–Ĺ–ł—Ź
|
| RSA
|
–Ē–ĺ 4096 –Ī–ł—ā
|
–®–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł–Ķ –ł –Ņ–ĺ–ī–Ņ–ł—Ā—Ć
|
2,7‚ÄĘ1028 –ī–Ľ—Ź –ļ–Ľ—é—á–į 1300 –Ī–ł—ā
|
–ě—Ā–Ĺ–ĺ–≤–į–Ĺ –Ĺ–į —ā—Ä—É–ī–Ĺ–ĺ—Ā—ā–ł –∑–į–ī–į—á–ł —Ą–į–ļ—ā–ĺ—Ä–ł–∑–į—Ü–ł–ł –Ī–ĺ–Ľ—Ć—ą–ł—Ö —á–ł—Ā–Ķ–Ľ; –ĺ–ī–ł–Ĺ –ł–∑ –Ņ–Ķ—Ä–≤—č—Ö –į—Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ—č—Ö –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–ĺ–≤. –í–ļ–Ľ—é—á–Ķ–Ĺ –≤–ĺ –ľ–Ĺ–ĺ–≥–ł–Ķ —Ā—ā–į–Ĺ–ī–į—Ä—ā—č
|
| ElGamal
|
–Ē–ĺ 4096 –Ī–ł—ā
|
–®–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł–Ķ –ł –Ņ–ĺ–ī–Ņ–ł—Ā—Ć
|
–ü—Ä–ł –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤–ĺ–Ļ –ī–Ľ–ł–Ĺ–Ķ –ļ–Ľ—é—á–į –ļ—Ä–ł–Ņ—ā–ĺ—Ā—ā–ĺ–Ļ–ļ–ĺ—Ā—ā—Ć —Ä–į–≤–Ĺ–į—Ź RSA, —ā.–Ķ. 2,7‚ÄĘ1028 –ī–Ľ—Ź –ļ–Ľ—é—á–į 1300 –Ī–ł—ā
|
–ě—Ā–Ĺ–ĺ–≤–į–Ĺ –Ĺ–į —ā—Ä—É–ī–Ĺ–ĺ–Ļ –∑–į–ī–į—á–Ķ –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź –ī–ł—Ā–ļ—Ä–Ķ—ā–Ĺ—č—Ö –Ľ–ĺ–≥–į—Ä–ł—Ą–ľ–ĺ–≤ –≤ –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–ľ –Ņ–ĺ–Ľ–Ķ; –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā –Ī—č—Ā—ā—Ä–ĺ –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–ĺ–≤–į—ā—Ć –ļ–Ľ—é—á–ł –Ī–Ķ–∑ —Ā–Ĺ–ł–∂–Ķ–Ĺ–ł—Ź —Ā—ā–ĺ–Ļ–ļ–ĺ—Ā—ā–ł. –ė—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –≤ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–Ķ —Ü–ł—Ą—Ä–ĺ–≤–ĺ–Ļ –Ņ–ĺ–ī–Ņ–ł—Ā–ł DSA-—Ā—ā–į–Ĺ–ī–į—Ä—ā–į DSS
|
| DSA
|
–Ē–ĺ 1024 –Ī–ł—ā
|
–Ę–ĺ–Ľ—Ć–ļ–ĺ –Ņ–ĺ–ī–Ņ–ł—Ā—Ć
|
|
–ě—Ā–Ĺ–ĺ–≤–į–Ĺ –Ĺ–į —ā—Ä—É–ī–Ĺ–ĺ—Ā—ā–ł –∑–į–ī–į—á–ł –ī–ł—Ā–ļ—Ä–Ķ—ā–Ĺ–ĺ–≥–ĺ –Ľ–ĺ–≥–į—Ä–ł—Ą–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –≤ –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–ľ –Ņ–ĺ–Ľ–Ķ; –Ņ—Ä–ł–Ĺ—Ź—ā –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –≥–ĺ—Ā. —Ā—ā–į–Ĺ–ī–į—Ä—ā–į –°–®–ź; –Ņ—Ä–ł–ľ–Ķ–Ĺ—Ź–Ķ—ā—Ā—Ź –ī–Ľ—Ź —Ā–Ķ–ļ—Ä–Ķ—ā–Ĺ—č—Ö –ł –Ĺ–Ķ—Ā–Ķ–ļ—Ä–Ķ—ā–Ĺ—č—Ö –ļ–ĺ–ľ–ľ—É–Ĺ–ł–ļ–į—Ü–ł–Ļ; —Ä–į–∑—Ä–į–Ī–ĺ—ā—á–ł–ļ–ĺ–ľ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ź–Ě–Ď.
|
| ECDSA
|
–Ē–ĺ 4096 –Ī–ł—ā
|
–®–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł–Ķ –ł –Ņ–ĺ–ī–Ņ–ł—Ā—Ć
|
–ö—Ä–ł–Ņ—ā–ĺ—Ā—ā–ĺ–Ļ–ļ–ĺ—Ā—ā—Ć –ł —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—Ć —Ä–į–Ī–ĺ—ā—č –≤—č—ą–Ķ, —á–Ķ–ľ —É RSA
|
–°–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ķ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–Ķ. –†–į–∑—Ä–į–Ī–į—ā—č–≤–į–Ķ—ā—Ā—Ź –ľ–Ĺ–ĺ–≥–ł–ľ–ł –≤–Ķ–ī—É—Č–ł–ľ–ł –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į–ľ–ł
|
–ü—Ä–ł–ľ–Ķ—á–į–Ĺ–ł—Ź
–õ–ł—ā–Ķ—Ä–į—ā—É—Ä–į
 |
|---|
| –ź–Ľ–≥–ĺ—Ä–ł—ā–ľ—č | |
|---|
| –Ę–Ķ–ĺ—Ä–ł—Ź | |
|---|
| –°—ā–į–Ĺ–ī–į—Ä—ā—č | |
|---|
| –Ę–Ķ–ľ—č | |
|---|