PROFILPELAJAR.COM

Следующие таблицы — списки 78 кубик первой классификации Ньютона^[1]^[2].

Класс I. Гиперболическая гипербола

Здесь описан класс I гиперболических гипербол, $a>0.$ (англ. Class I. Redundant Hyperbolas^[2]).^[3]

Гиперболическая гипербола

xy^{2}+ey=ax^{3}+bx^{2}+cx+d,\quad

a>0,

имеет три обыкновенные асимптоты

x=0,\quad

y=\pm {\sqrt {a}}\left(x+{\frac {b}{2a}}\right),

пересекающиеся в вершинах следующего асимптотического треугольника^[4]:

\left(0,\;{\frac {b}{2{\sqrt {a}}}}\right),

\left(0,\;-{\frac {b}{2{\sqrt {a}}}}\right),

\left(-{\frac {b}{2a}},\;0\right).

Гиперболическая гипербола пересекает три свои асимптоты на конечном расстоянии в следующих трёх точках (у Смогоржевского и Столовой опечатка: в ординате не хватает множителя $\mp {\sqrt {a}}$ )^[5], лежащих на одной прямой^[6]:

\left(0,\;{\frac {d}{e}}\right),\;\left({\frac {4ad\pm 2be{\sqrt {a}}}{b^{2}-4ac\mp 4ae{\sqrt {a}}}},\;\mp {\sqrt {a}}{\frac {8a^{2}d+b^{3}-4abc}{2a(b^{2}-4ac\mp 4ae{\sqrt {a}})}}\right).

Род 1. Адиаметралъная гиперболическая гипербола

Здесь представлена таблица со списком рода 1 адиаметралъных гиперболических гипербол, $e\neq 0$ . Будем также полагать, что $b\neq 0$ (англ. Genus 1. Adiametral Redundant Hyperbolas^[2])^[7].

Адиаметралъная гиперболическая гипербола (без диаметров) имеет характеристическое уравнение

ax^{4}+bx^{3}+cx^{2}+dx+{\frac {1}{4}}e^{2}=0,\quad

e\neq 0,

а также $b\neq 0,$ и пусть $x_{1},\;x_{2},\;x_{3},\;x_{4}$ — его корни^[4].

Рассматривая уравнение гиперболической гиперболы как квадратное относительно $y,$ получаем:

y={\frac {-e\pm 2{\sqrt {ax^{4}+bx^{3}+cx^{2}+dx+{\frac {1}{4}}e^{2}}}}{2x}}=

={\frac {-e\pm 2{\sqrt {a(x-x_{1})(x-x_{2})(x-x_{3})(x-x_{4})}}}{2x}},

где действительное или мнимое значение переменной $y$ определяет знак подкоренного выражения, то есть знак левой части уравнения гиперболической гиперболы^[4].

Отметим следующую гиперболу и её свойства^[5]:

y=-{\frac {e}{2x}}:

эта гипербола делит пополам каждую хорду адиаметралъной гиперболической гиперболы, перпендикулярную к оси абсцисс;
эта гипербола пересекает адиаметралъную гиперболическу гиперболу в следующих точках и только в них:

(x_{1},\;-{\frac {e}{2x_{1}}}),(x_{2},\;-{\frac {e}{2x_{2}}}),(x_{3},\;-{\frac {e}{2x_{3}}}),(x_{4},\;-{\frac {e}{2x_{3}}}).

Существует девять разных адиаметралъных гиперболических гипербол, описанных в следующей таблице^[8].

Адиаметралъные гиперболические гиперболы, $e\neq 0$ , $b\neq 0$
№	Описание^[7]	Изображение, $e>0$
1	1. Все корни характеристического уравнения — различные действительные одного знака, например, $0<x_{1}<x_{2}<x_{3}<x_{4}$ На графике овал находится внутри асимптотического треугольника.
2	2. Все корни характеристического уравнения — действительные и различные, два положительны, два отрицательны, например, $x_{1}<x_{2}<0<x_{3}<x_{4}.$
3	3. Все корни характеристического уравнения — действительные, два равны и больше или меньше остальных разных корней с другим знаком, например, $x_{1}=x_{2}<0<x_{3}<x_{4}.$
4	4. Все корни характеристического уравнения — действительные одного знака, два равны и больше или меньше остальных разных корней, например, $0<x_{1}<x_{2}<x_{3}=x_{4}.$ На графике точка самопересечения лежит внутри асимптотического треугольника.
5	5. Все корни характеристического уравнения — действительные одного знака, два равны и больше одного и меньше другого остальных разных корней, например, $0<x_{1}<x_{2}=x_{3}<x_{4}.$ На графике изолированная точка $\left(x_{2},-{\frac {e}{2x_{2}}}\right)$ лежит внутри асимптотического треугольника.
6	6. Все корни характеристического уравнения — действительные, три равны, например, $x_{1}=x_{2}=x_{3}<x_{4}.$ На графике касп $\left(x_{1},-{\frac {e}{2x_{1}}}\right)$ лежит внутри асимптотического треугольника.
7	7. Все корни характеристического уравнения — разные, два действительных, два комплексно сопряжённых, например, $x_{1}>x_{2},\;x_{3,\;4}=\alpha \pm \beta i.$ Имеем: $y={\frac {-e\pm 2{\sqrt {a(x-x_{1})(x-x_{2})((x-\alpha )^{2}+\beta ^{2})}}}{2x}}.$
8	8. Два корня характеристического уравнения — равные действительные, два комплексно сопряжённых, например, $x_{1}=x_{2},\;x_{3,\;4}=\alpha \pm \beta i.$
9	9. Все корни характеристического уравнения — комплексные попарно сопряжённые, например, $x_{1,\;2}=\alpha _{1}\pm \beta _{1}i,\;x_{3,\;4}=\alpha _{2}\pm \beta _{2}i.$

Род 2. Монодиаметралъная гиперболическая гипербола

Здесь представлена таблица со списком рода 2 монодиаметралъных гиперболических гипербол, $e=0$ , $b\neq 0$ , $b^{2}\neq 4ac$ (англ. Genus 2. Monodiametral Redundant Hyperbolas^[2])^[9].

Монодиаметралъная гиперболическая гипербола имеет один диаметр

y=0

и характеристическое уравнение

ax^{4}+bx^{3}+cx^{2}+dx=0,\quad

b\neq 0,\quad

b^{2}\neq 4ac

и пусть $x_{1},\;x_{2},\;x_{3},\;x_{4}$ — его корни^[4].

Ньютон относит к этому роду двенадцать разных монодиаметралъных гиперболических гипербол, описанных в следующей таблице^[8].

Монодиаметралъные гиперболические гиперболы, $b\neq 0,$ $b^{2}\neq 4ac$
№	Описание^[9]	Изображение, $b<0$
10	1. Все корни характеристического уравнения — различные действительные одного знака, например, $x_{1}=0<x_{2}<x_{3}<x_{4}.$ На графике овал находится внутри асимптотического треугольника.
11	2. Все корни характеристического уравнения — различные действительные разных знаков и $\|x_{1}\|>x_{3}+x_{4},$ например, $x_{1}<x_{2}=0<x_{3}<x_{4}.$
12	3. Все корни характеристического уравнения — различные действительные разных знаков и $\|x_{1}\|<x_{3}+x_{4},$ например, $x_{1}<x_{2}=0<x_{3}<x_{4}.$
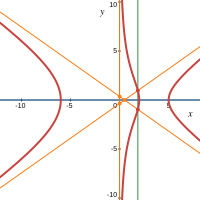
13	4. Два отрицательных корня характеристического уравнения равны, меньше различных неотрицательных и $\|x_{1}\|>0{,}5x_{4},$ например, $x_{1}=x_{2}<x_{3}=0<x_{4}.$
14	5. Два отрицательных корня характеристического уравнения равны, меньше различных неотрицательных и $\|x_{1}\|<0{,}5x_{4},$ например, $x_{1}=x_{2}<x_{3}=0<x_{4}.$
15	6. Все корни характеристического уравнения — действительные одного знака, кратный корень больше третьего и меньше четвёртого, например, $x_{1}=0<x_{2}=x_{3}<x_{4}.$ На графике изолированная точка $(x_{2},\;0)$ лежит внутри асимптотического треугольника.
16	7. Все корни характеристического уравнения — действительные одного знака, кратный корень больше разных остальных, например, $x_{1}=0<x_{2}<x_{3}=x_{4}.$ На графике точка самопересечения $(x_{3},\;0)$ лежит внутри асимптотического треугольника.
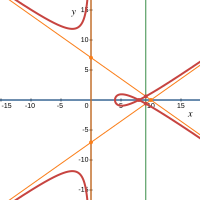
17	8. Все корни характеристического уравнения — действительные, три равны, например, $x_{1}=0<x_{2}=x_{3}=x_{4}.$ На графике касп $(x_{2},0)$ лежит внутри асимптотического треугольника.
18	9. Все корни характеристического уравнения — разные, два действительных, два комплексно сопряжённых, например, $x_{1}=0>x_{2},\;x_{3,\;4}=\alpha \pm \beta i,$ $x_{2}$ и $\alpha$ одинаковых знаков, причём $\|x_{2}\|\leqslant 2\|\alpha \|.$ Имеем: $y={\frac {\pm 2{\sqrt {a(x-x_{1})(x-x_{2})((x-\alpha )^{2}+\beta ^{2})}}}{2x}}.$
19	10. Все корни характеристического уравнения — разные, два действительных, два комплексно сопряжённых, например, $x_{1}=0>x_{2},\;x_{3,\;4}=\alpha \pm \beta i,$ $x_{2}$ и $\alpha$ одинаковых знаков, причём $\|x_{2}\|>2\|\alpha \|.$
20	11. Все корни характеристического уравнения — разные, два действительных, два комплексно сопряжённых, например, $x_{1}=0>x_{2},\;x_{3,\;4}=\alpha \pm \beta i,$ $x_{2}$ и $\alpha$ разных знаков, причём $\|x_{2}\|<2\|\alpha \|$ и $x_{2}(x_{2}-4\alpha )<4\beta ^{2}.$ При $\|x_{2}\|=2\|\alpha \|$ имеем $b=0$ , то есть гиперболическая гипербола имеет род 4.
21	12. Все корни характеристического уравнения — разные, два действительных, два комплексно сопряжённых, например, $x_{1}=0>x_{2},\;x_{3,\;4}=\alpha \pm \beta i,$ $x_{2}$ и $\alpha$ разных знаков, причём $\|x_{2}\|<2\|\alpha \|$ и $x_{2}(x_{2}-4\alpha )>4\beta ^{2}.$

Род 3. Тридиаметралъная гиперболическая гипербола

Здесь представлена таблица со списком рода 3 тридиаметралъных гиперболических гипербол, $e=0$ , $b^{2}=4ac$ (англ. Genus 3. Tridiametral Redundant Hyperbolas^[2])^[10].

Тридиаметралъная гиперболическая гипербола при $b=-2{\sqrt {ac}}$ имеет три диаметра

y=0,\quad

y=-3x{\sqrt {a}}+{\sqrt {c}},\quad

y=3x{\sqrt {a}}-{\sqrt {c}}

и характеристическое уравнение

ax^{4}+bx^{3}+cx^{2}+dx=0,\quad

b^{2}=4ac,

и пусть $x_{1},\;x_{2},\;x_{3},\;x_{4}$ — его корни^[11].

Это характеристическое уравнение имеет комплексные корни. Пусть $x_{1}=r\neq 0,\;$ $x_{2,4}=\alpha \pm \beta i,\;$ $x_{4}=0.$ В этих условиях получаем следующее уравнение гиперболической гиперболы^[11]:

xy^{2}=a(x^{3}-(2\alpha +r)x^{2}+(\alpha ^{2}+\beta ^{2}+2\alpha r)x-(\alpha ^{2}+\beta ^{2})r).

Перепишем условие $b^{2}=4ac:$

(2\alpha +r)^{2}=4(\alpha ^{2}+\beta ^{2}+2\alpha r),\quad

r^{2}-4\alpha r-4\beta ^{2}=0.

откуда получаем следующее выражение для $r$ , решая квадратное уравнение^[11]:

r=2(\alpha \pm {\sqrt {\alpha ^{2}+\beta ^{2}}}).

Ньютон относит к этому роду два вида разных тридиаметралъных гиперболических гипербол, описанных в следующей таблице^[8]^[11]. Для первого вида переменные $r$ и $a$ имеют одинаковые знаки, для второго — разные^[12].

Тридиаметралъные гиперболические гиперболы, $b^{2}=4ac$
№	Описание^[7]	Изображение, $\alpha >0$
22	1. Например, корни характеристического уравнения — $x_{1}=2(\alpha +{\sqrt {\alpha ^{2}+\beta ^{2}}}),\;$ $x_{2,4}=\alpha \pm \beta i,\;$ $x_{4}=0,$ где $\alpha >0.$
23	2. Например, корни характеристического уравнения — $x_{1}=2(\alpha -{\sqrt {\alpha ^{2}+\beta ^{2}}}),\;$ $x_{2,4}=\alpha \pm \beta i,\;$ $x_{4}=0,$ где $\alpha >0.$

Род 4. Гиперболическая гипербола с асимптотами, пересекающимися в одной точке

Здесь представлена таблица со списком рода 4 гиперболических гипербол с асимптотами, пересекающимися в одной точке, $b=0$ (англ. Genus 1. Redundant Hyperbolas with asymptotes concurrent^[2]). Эти кривые получаются стягиванием в точку асимптотического треугольника у адиаметралъных, монодиаметралъных и тридиаметральны гиперболических гипербол, всего девять случаев^[12].

Гиперболические гиперболы с асимптотами, пересекающимися в одной точке, $b=0$
№	Описание^[12]	Изображение
Адиаметралъные гиперболические гиперболы, $e\neq 0$
24	1. Получается из типа 7 рода 1. Все корни характеристического уравнения — разные, два действительных, два комплексно сопряжённых, например, $x_{1}>x_{2},\;x_{3,\;4}=\alpha \pm \beta i.$ Имеем: $y={\frac {-e\pm 2{\sqrt {a(x-x_{1})(x-x_{2})((x-\alpha )^{2}+\beta ^{2})}}}{2x}}.$
25	2. Получается из типа 3 (или 8) рода 1. Все корни характеристического уравнения — действительные, два равны и больше или меньше остальных разных корней с другим знаком, например, $x_{1}=x_{2}<0<x_{3}<x_{4}.$
26	3. Получается из типа 2 (или 9) рода 1. Все корни характеристического уравнения — действительные и различные, два положительны, два отрицательны, например, $x_{1}<x_{2}<0<x_{3}<x_{4}.$ График адиаметралъной гиперболической гиперболы не проходит через точку пересечения асимптот.
27	4. Получается из типа 2 (или 9) рода 1. Все корни характеристического уравнения — действительные и различные, два положительны, два отрицательны, например, $x_{1}<x_{2}<0<x_{3}<x_{4}.$ График адиаметралъной гиперболической гиперболы проходит через точку пересечения асимптот.
Монодиаметралъные гиперболические гиперболы, $e=0,$ $c\neq 0$
Тридиаметралъные гиперболические гиперболы, $e=c=0$

Примечания

↑ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 7—28.
↑ ¹ ² ³ ⁴ ⁵ ⁶ Ball W. W. Rouse Newton's classification of cubic curves, 1891, 38.
↑ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 7—17.
↑ ¹ ² ³ ⁴ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 9.
↑ ¹ ² Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 10.
↑ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 28.
↑ ¹ ² ³ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 9—13.
↑ ¹ ² ³ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 8.
↑ ¹ ² Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 13—16.
↑ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 16—17.
↑ ¹ ² ³ ⁴ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 16.
↑ ¹ ² ³ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 17.

Источники

Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка. М.: Физматлит, 1961. 271 с., ил.
Ball W. W. Rouse^[англ.] Newton's classification of cubic curves, Proc. London Math. Soc. 1891. Vol. 50, Iss. 2. P. 35–40.

[_cb5f5302b720f580-1] Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 7—28.

[_957e5f494fc2a78e-2] ¹ ² ³ ⁴ ⁵ ⁶ Ball W. W. Rouse Newton's classification of cubic curves, 1891, 38.

[_1d3859f9c76ba666-3] Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 7—17.

[_b59a1c0eec9d098e-4] ¹ ² ³ ⁴ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 9.

[_437acd1df01bd006-5] ¹ ² Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 10.

[_c57d01362b90387d-6] Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 28.

[_788621c43da4f020-7] ¹ ² ³ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 9—13.

[_c0c27f0ef3a3d975-8] ¹ ² ³ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 8.

[_3594619ddfe35e68-9] ¹ ² Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 13—16.

[_811e0f0db2f96e96-10] Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 16—17.

[_768d971e0cc92424-11] ¹ ² ³ ⁴ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 16.

[_80f6aa1e132c91eb-12] ¹ ² ³ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 17.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]