Симплектическое пространство
|
Read other articles:

1270–1974 state in the Horn of Africa For the commonly used exonym, see Abyssinia. Ethiopian Empireመንግሥተ ኢትዮጵያ (Ge'ez)Mängəśtä ʾItyop̣p̣yaየኢትዮጵያ ንጉሠ ነገሥት መንግሥት (Amharic)Yäʾityop̣p̣ya Nägusä Nägäst Mängəśt1270–19741936–1941: Government-in-exile Top: Civil FlagBottom: State Flag Coat of arms Motto: ኢትዮጵያ ታበፅዕ እደዊሃ ኀበ እግዚአብሔርItyopia tabetsih edewiha ḫabe I...

NEC Nimègue Généralités Nom complet Nijmegen Eendracht Combinatie Fondation 15 novembre 1900 Couleurs Noir, rouge et vert Stade McDOS Goffertstadion (12 500 places) Siège Stadionplein 1Postbus 65626503 GB Nijmegen Championnat actuel Eredivisie Président Ron van Oijen Entraîneur Rogier Meijer Site web http://www.nec-nijmegen.nl Maillots Domicile Extérieur Actualités Pour la saison en cours, voir : Eredivisie 2023-20240modifier N.E.C., abréviation de Nijmegen Eendracht...

Возможно, эта статья содержит оригинальное исследование. Проверьте соответствие информации приведённым источникам и удалите или исправьте информацию, являющуюся оригинальным исследованием. В случае необходимости подтвердите информацию авторитетными источниками. В �...

Book of Psalms, chapter 51 This article is about the penitential psalm. For the musical settings based on the psalm, see Miserere (disambiguation) § Music. This article is about Psalm 51 in Hebrew (Masoretic) numbering. For Psalm 51 in Greek Septuagint or Latin Vulgate numbering, see Psalm 52. Psalm 51Have mercy upon me, O GodPenitential PsalmLatin text on a holy water font: see verse 9 belowOther name Psalm 50 Miserere mei, Deus LanguageHebrew (original) Psalm 51, one of the penitentia...
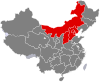
Cet article est une ébauche concernant un aéroport chinois. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Aéroport international de Nanning Wuxu南宁吴圩国际机场 Localisation Pays Chine Province Guangxi Ville Nanning Coordonnées 22° 36′ 30″ nord, 108° 10′ 21″ est Altitude 128 m (420 ft) Informations aéronautiques Code IATA NNG Code OACI ZGNN Type d'aéroport ...

Come leggere il tassoboxArvicola di Fatio Stato di conservazione Rischio minimo Classificazione scientifica Dominio Eukaryota Regno Animalia Phylum Chordata Classe Mammalia Sottoclasse Theria Infraclasse Eutheria Superordine Euarchontoglires (clade) Glires Ordine Rodentia Sottordine Myomorpha Superfamiglia Muroidea Famiglia Cricetidae Sottofamiglia Arvicolinae Genere Microtus Specie M. multiplex Nomenclatura binomiale Microtus multiplexFatio, 1905 L'arvicola di Fatio (Microtus multiplex Fati...

American legislative district Map of Massachusetts House of Representatives' 4th Hampden district, based on the 2010 United States census. Massachusetts House of Representatives' 4th Hampden district in the United States is one of 160 legislative districts included in the lower house of the Massachusetts General Court. It covers the city of Westfield in Hampden County.[1][2] Democrat John Velis of Westfield represented the district from 2014 to 2020.[3] Candidates for ...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

American insurance company For other uses, see Unum (disambiguation). Unum GroupFormerlyUnion Mutual (1848–1986)Unum Corporation (1986–1999)UnumProvident Corporation (1999–2007)Company typePublic companyTraded asNYSE: UNMS&P 400 componentISINUS91529Y1064IndustryEmployee group benefits (disability, dental, life and critical illness insurance)Founded1848; 176 years ago (1848)HeadquartersChattanooga, Tennessee, U.S.Key peopleRick McKenney, President and CEO Kevin...

Cet article est une ébauche concernant les réserves naturelles et autres zones protégées, le bois et la forêt, l’Utah et le Wyoming. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Forêt nationale d'AshleyGéographiePays États-UnisComté comté de SweetwaterComté comté d'UtahComté comté de UintahComté comté de SummitComté comté de DuchesneComté comté de DaggettCoordonnées 40° 20�...

Changes in calendar conventions from Julian to Gregorian dates Old Style and New Style redirect here. For other meanings of the old style, see Old Style (disambiguation). For other meanings of the new style, see The New Style. This article is about the 18th-century changes in calendar conventions used by Great Britain and its colonies, together with a brief explanation of usage of the term in other contexts. For a more general discussion of the equivalent transitions in other countries, see A...

جيك بغ معلومات شخصية اسم الولادة (بالإنجليزية: Jacob Edwin Kennedy Bugg) الميلاد 28 فبراير 1994 (العمر 30 سنة)نوتينغهام مواطنة المملكة المتحدة الطول 170 سنتيمتر الحياة العملية المهنة مغن مؤلف، وعازف قيثارة، وعازف بيانو، وموسيقي اللغة الأم الإنجليزية اللغات الإ...

الحياة في السعودية الثقافة الثقافة المطبخ السينما الأعياد الرياضة الدين التاريخ العَلم المجتمع السكان اللغات الصحة التعليم العالي الإعلام جرائم البدون الحكومة حقوق الإنسان الجيش مجلس الشورى مجلس الوزراء العلاقات الخارجية الدستور القانون السياسة السياسة الإعدام القضا�...

Football match1932 FA Cup finalOfficial programmeEvent1931–32 FA Cup Newcastle United Arsenal 2 1 Date23 April 1932VenueWembley Stadium, LondonRefereeW. P. HarperAttendance92,298← 1931 1933 → The 1932 FA Cup final was contested by Newcastle United and Arsenal at Wembley Stadium in what became known as the Over The Line final. Newcastle won 2–1, both of their goals scored by Jack Allen. Arsenal had led 1–0 with a Bob John goal, but Newcastle's equaliser came after a long bal...

كرة السلة في الألعاب الأولمبية الصيفية 2004معلومات عامةجزء من الألعاب الأولمبية الصيفية 2004 الرياضة كرة السلة البلد اليونان المكان O.A.C.A. Olympic Indoor Hall (en) بتاريخ 2004 تاريخ البدء 15 أغسطس 2004 تاريخ الانتهاء 28 أغسطس 2004 لديه جزء أو أجزاء كرة السلة في الألعاب الأولمبية الصيفية 2004 – منا�...

روبيه شعار الشعار:(باللاتينية: Probitas Industria) الاسم الرسمي (بالفرنسية: Roubaix) الإحداثيات 50°41′24″N 3°10′54″E / 50.69°N 3.1816666666667°E / 50.69; 3.1816666666667 [1] [2] تقسيم إداري البلد فرنسا[3][4] التقسيم الأعلى ليل خصائص جغرافية المساحة 1...

American politician John Gadsdenportrait by Charles Fraser28th Mayor of CharlestonIn office1827–1829Preceded byJoseph JohnsonSucceeded byHenry L. Pinckney Personal detailsBorn(1787-03-04)March 4, 1787Charleston, South CarolinaDiedJanuary 24, 1831(1831-01-24) (aged 43)Charleston, South CarolinaSpouseAnn Margaret EdwardsRelativesChristopher Gadsden (grandfather)Christopher Edwards Gadsden (brother)James Gadsden (brother)ProfessionLawyer John Gadsden (March 4, 1787 – January 24, 1831) w...

Salvadoran writer and politician (1863-1955) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Francisco Gavidia – news · newspapers · books · scholar · JSTOR (April 2007) (Learn how and when to remove this message) In this Spanish name, the first or paternal surname is Gavidia and the second or matern...

This article is about the Mexican state. For that state's capital city, see San Luis Potosí (city). For the Bolivian city, see Potosí. For the football team, see San Luis F.C. State of Mexico State in MexicoSan Luis PotosíStateFree and Sovereign State of San Luis PotosíEstado Libre y Soberano de San Luis Potosí (Spanish)Xikia'ani t'i to'ome teenek San Luis Potosí (Huastec)View of Friar's Hill near Matehuala Coat of armsState of San Luis Potosí within MexicoCoordinates: 22°36′N 100°...

Questa voce sull'argomento cestisti statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Mitchell WattNazionalità Stati Uniti Altezza208 cm Peso107 kg Pallacanestro RuoloCentro Squadra Saragozza CarrieraGiovanili Desert Edge High School2008-2012 Buffalo Bulls Squadre di club 2012-2013 Hap. Gilboa G.E.24 (240)2013-2014 Ironi Nes Ziona29 (408)2014 S.C. Warriors9 (42...









































![{\displaystyle \left\langle u,w\right\rangle =\operatorname {Im} \left[u,w\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aee1719649c391a34c63eaa0f711597dbbc78b1)
![{\displaystyle \left[\cdot ,\cdot \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dbd62035834752b172b9d64026683da05d6eccb)




