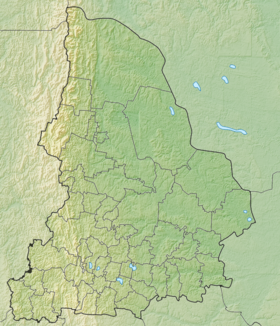
Северский дендросад
| |||||||||||||||||||||||||||
Read other articles:

Ptolemaios I Epigonos [1] (bahasa Yunani: Πτολεμαίος ὁ ἐπίγονος Ptolemaios Epigonos, Epigonos yakni Pewaris,[2] 299/298 SM[3]–Februari 240 SM[4]) adalah seorang Pangeran Yunani dari Asia Kecil, keturunan Makedonia dan Thessalia. Latar belakang keluarga Patung dada Lysimakhos di Museum Arkeologi Efesus (bahasa Turki: Efes Müzesi), Turki. Ptolemaios I adalah putra pertama[5] dari Lysimakhos dan Arsinoe II, memiliki dua oran...

Keuskupan Agung BaghdadArchdioecesis Bagdathensis LatinorumKatedral Santo Yosef, BaghdadLokasiNegara IrakMetropolitTunduk langsung pada Takhta SuciInformasiRitusRitus LatinKepemimpinan kiniPausFransiskusUskupJean Benjamin Sleiman, O.C.D.Keuskupan Agung Baghdad (bahasa Latin: Bagdathen(sis) Latinorum) adalah wilayah keuskupan agung dari Gereja Katolik Ritus Latin.[1][2] Terdiri dari 2.500 paroki di seluruh wilayah Irak dan merupakan satu-satunya keuskupan Ritus La...

Di bawah ini adalah daftar kementerian dan susunan organisasi kementerian negara di Republik Indonesia. Kementerian Kementerian kelompok I Menurut Peraturan Presiden Nomor 7 Tahun 2015 tentang Organisasi Kementerian Negara, kementerian kelompok I adalah kementerian yang menangani urusan pemerintahan yang nomenklatur kementeriannya secara tegas disebutkan dalam UUD 1945.[1] Logo Kementerian / Lembaga Susunan Organisasi Pemimpin Eselon[2] Dasar Hukum Kementerian Dalam Negeri[...

Kementerian Lingkungan Hidup Republik Korea환경부環境部Hwan-gyeong-buInformasi lembagaDibentuk24 Desember 1994[1]Wilayah hukumPemerintah Korea SelatanKantor pusatKompleks Pemerintah Sejong, Kota Sejong, Korea SelatanMenteriKim Eun-kyung, Menteri Lingkungan HidupLee Jung-sup, Wakil MenteriSitus webSitus resmi Kantor pusat di Kota Sejong Kementerian Lingkungan Hidup Republik Korea adalah badan kementerian di bawah naungan pemerintah Korea Selatan yang bertugas memberikan perlindun...

Website about bitcoin and digital currencies, owned by Digital Currency Group CoinDeskType of businessSubsidiaryHeadquartersNew York, NY, U.S.Area servedWorldwideFounder(s)Shakil KhanEditorMarc HochsteinIndustryDigital currencyParentDigital Currency Group (2016–23)Bullish (2023–present)URLcoindesk.comLaunchedMay 2013; 10 years ago (2013-05) CoinDesk is a news site specializing in bitcoin and digital currencies. Founded by Shakil Khan, the firm also provides gui...

Town and borough in West Sussex, England For other uses, see Crawley (disambiguation). Town and non-metropolitan borough in EnglandCrawleyTown and non-metropolitan boroughBorough of CrawleyThe High Street, Queen's Square, Goff's Park House and the Memorial Gardens with the centre in the background Coat of Arms of the Borough CouncilMotto(s): I Grow and I RejoiceLocation of Crawley within West SussexCoordinates: 51°6′33″N 0°11′14″W / 51.10917°N 0.18722°W...

Swedish painter (1662–1727) This copperplate engraving by Alexander Bannerman, printed in Walpole's Anecdotes, is the only known portrait of the portrait painter Boit. Charles Boit (10 August 1662, in Stockholm – 6 February 1727, in Paris) was a Swedish painter in vitreous enamels who mostly worked in England, Austria and France. Biography Boit was born in a Huguenot family in Stockholm, the son of a merchant who was also master of the royal indoor tennis court. He became a goldsmith's ap...

12th/13th century crusades around the Baltic Sea For the film, see Northern Crusades (film). Battle on the Ice on Lake Peipus during the Northern Crusades, miniature from the Illustrated Chronicle of Ivan the Terrible (16th century) vteCrusadesIdeology and institutions Crusading movement In the Holy Land (1095–1291) First 1101 Norwegian Venetian 1129 Second Third 1197 Fourth Fifth Sixth Barons' Seventh 1267 Catalan Eighth Lord Edward's Fall of Outremer Later Crusades (1291–1717) C...

Carlo Ancelotti became the first manager to win nine UEFA competition titles. This is a list of UEFA club competition winning football managers. It includes victories in the European Cup and UEFA Champions League, the UEFA Cup Winners' Cup, the UEFA Cup and Europa League, the UEFA Europa Conference League, the UEFA Intertoto Cup, the UEFA Super Cup and the Intercontinental Cup. Italian Carlo Ancelotti is the most successful manager, claiming 9 titles. Italian managers have won more tournamen...

Правительство Юга России Правительство Юга России. Крым, Севастополь, 1920 Общая информация Страна Россия Дата создания 11 апреля 1920 года Предшественник Южнорусское правительство Дата упразднения 11 ноября 1920 года Заменено на Русский совет Руководство Ответственный минис...

Scuba cave diving incident in South Australia Mount Gambier cave diving accidentDate28 May 1973 (1973-05-28)Time~1:30 pmLocationThe Shaft (sinkhole near Mount Gambier, South Australia)CauseLost exploring caveParticipantsJohn H. Bockerman, Peter S. Burr, Christine M. Millott, Glen Millott, Stephen Millott, Larry Reynolds, Gordon G. Roberts, Robert J. Smith, Joan Harper (did not dive)OutcomeDeaths of Stephen and Christine Millott, Gordon G. Roberts, and John H. Bockerman The 1973...

US record label Scepter RecordsParent companyGusto RecordsFounded1959 (1959)FounderFlorence GreenbergGenrePop, soulCountry of originU.S.LocationNew York City Scepter Records was an American record company founded in 1959 by Florence Greenberg. History Florence Greenberg founded Scepter Records from the $4,000 she received after she sold Tiara Records and the Shirelles to Decca Records. When the Shirelles didn't produce any hits for Decca, they were given back to Greenberg, who promptly s...

2019–2020 political party in South Korea Not to be confused with New Conservative Party for Reform. New Conservative Party 새로운보수당LeaderYoo Seong-minFoundedSeptember 30, 2019 (2019-09-30) (as Emergency Action for Change and Innovation)December 12, 2019 (2019-12-12) (as New Conservative Party)DissolvedFebruary 17, 2020 (2020-02-17)Split fromBareunmirae PartyMerged intoUnited Future PartyIdeologyConservatism (South Korean)Polit...

Este artículo se refiere o está relacionado con una infraestructura de transporte público futura o en desarrollo. La información de este artículo puede cambiar frecuentemente. Por favor, no agregues datos especulativos y recuerda colocar referencias a fuentes fiables para dar más detalles. Cercanías de Lérida Operador Rodalies de Catalunya (Renfe) FGC Tipos servicio Cercanías Territorio cubierto Las Garrigas, Noguera, Plana de Urgel, Segarra, Segriá y Urgel Líneas 6 Anch...

In meccanica celeste, l'asse nodale o linea dei nodi è la linea d'intersezione del piano di un'orbita con un piano di riferimento, come per esempio il piano equatoriale o il piano eclittico. I due punti dell'orbita dati dall'intersezione tra questi due piani vengono detti nodi dell'orbita. Si distinguono: il nodo ascendente: è il punto in cui l'oggetto interseca il piano di riferimento passando dall'emisfero meridionale all'emisfero settentrionale; il nodo discendente: è il punto in cui l'...

Decision-making body of the Eswatini government Politics of Eswatini Constitution Human rights LGBT rights Monarchy Ngwenyama (list) Mswati III Ndlovukati (list) Ntfombi Government Prime Minister Russell Dlamini Cabinet Parliament Senate President House of Assembly Speaker Administrative divisions Regions TinkhundlaUmphakatsi Elections Recent elections General: 201320182023 Political parties Foreign relations Ministry of Foreign Affairs and International Cooperation Minister: Thuli Dladla Dip...

Upsilon Andromedae cKesan seniman tentang inspirasi Upsilon Andromedae c.PenemuanDitemukan olehMarcy et al.Situs penemuanCalifornia and Carnegie Planet Search USATanggal penemuanApril 15, 1999Metode deteksiRadial velocityCiri-ciri orbitApastron~9.11 GmPeriastron~91.6 GmSumbu semimayor~124.1 GmEksentrisitas0.260±0.079[1]Periode orbit241.26±0.64[1] d~0.66228[1] yInklinasi7.868 ± 1.003[2]Bujur node menaik236.853 ± 7.528[2]Waktu peri...

Argentine tennis player Santiago Rodríguez TavernaRodríguez Taverna at the 2022 French OpenCountry (sports) ArgentinaBorn (1999-07-16) 16 July 1999 (age 24)Buenos Aires, ArgentinaHeight1.91 m (6 ft 3 in)Turned pro2016PlaysRight-handed (two-handed backhand)CoachGuillermo FrancoPrize moneyUS$ 396,664SinglesCareer record0–1 (0% in ATP Tour and Grand Slam main draw matches, and in Davis Cup)Career titles0Highest rankingNo. 157 (29 August ...

Гимн Грузинской ССРгруз. საქართველოს სსრ სახელმწიფო ჰიმნიСакартвелос сабчота республикис химни Нотная страница Автор слов Григол Абашидзе и Александр Абашели, 1944 Композитор Отар Тактакишвили, 1944 Грузия Грузия Утверждён 1944 году Отменён 1990 году Госуд�...

Góc thiên đỉnh Mặt Trời là góc giữa các tia song song của Mặt Trời và phương thẳng đứng. Nó là góc phụ với góc cao Mặt Trời, tức là góc chiếu của các tia Mặt Trời so với phương nằm ngang (chân trời), vì thế cosin của góc này là sin của góc kia. Các góc này có thể được tính bằng cùng một công thức, suy ra từ các kết quả của lượng giác cầu.[1][2] Vào thời điểm trưa M...