Риманова геометрия
|
Read other articles:

Penyembahan Anak Lembu Emas karya Nicolas Poussin Keluaran 32 (disingkat Kel 32) adalah bagian dari Kitab Keluaran dalam Alkitab Ibrani dan Perjanjian Lama di Alkitab Kristen. Termasuk dalam kumpulan kitab Taurat yang disusun oleh Musa.[1][2] Teks Naskah sumber utama: Masoretik, Taurat Samaria, Septuaginta dan Naskah Laut Mati. Pasal ini terdiri dari 35 ayat. Berisi kisah tragis penyembahan patung anak lembu emas (עגל הזהב Egel haZahav) dan akibatnya. Dalam Ibrani, keja...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2012. Ardei umpluţi Ardei umpluţi (pengucapan bahasa Rumania: [arˈdej umˈplut͡sʲ] ) adalah paprika yang diisi dengan daging (biasanya babi), nasi, bawang, serta sayur dan bumbu lainnya. Makanan ini sangat mirip dengan punjene paprike di Serbia atau ...

ChimneysPenulisAgatha ChristiePementasan perdana16 Oktober 2003Bahasa asliInggris Chimneys adalah sebuah drama karya penulis kejahatan Agatha Christie dan berdasarkan pada novel tahun 1925 buatannya sendiri The Secret of Chimneys. Drama tersebut ditulis pada 1931 dan dibuka di Embassy Theatre di Swiss Cottage pada Desember tahun tersebut. Setahun sebelumnya, Black Coffee, drama panggung pertama buatan Christie yang ditampilkan, telah dibuka di teater yang sama. Pranala luar [1] Sunday Herald ...
See also: Index of religion-related articles Overview of and topical guide to religion The following outline is provided as an overview of and topical guide to religion: Religion – organized collection of beliefs, cultural systems, and world views that relate humanity to an order of existence. Many religions have narratives, symbols, and sacred histories that are intended to explain the meaning of life and/or to explain the origin of life or the Universe. From their beliefs about the co...

Chemical compound SKF-82,958Identifiers IUPAC name 3-allyl-6-chloro-1-phenyl-1,2,4,5-tetrahydro-3-benzazepine-7,8-diol CAS Number80751-65-1PubChem CID1225ChemSpider1188UNII7W60FE897QChEMBLChEMBL317741CompTox Dashboard (EPA)DTXSID70894837 Chemical and physical dataFormulaC19H20ClNO2Molar mass329.82 g·mol−13D model (JSmol)Interactive image SMILES C=CCN1CCC2=C(C(=C(C=C2C(C1)C3=CC=CC=C3)O)O)Cl SKF-82,958 is a synthetic compound of the benzazepine class that acts as a D1/D5 receptor full a...

ロバート・デ・ニーロRobert De Niro 2011年のデ・ニーロ生年月日 (1943-08-17) 1943年8月17日(80歳)出生地 アメリカ合衆国・ニューヨーク州ニューヨーク市身長 177 cm職業 俳優、映画監督、映画プロデューサージャンル 映画、テレビドラマ活動期間 1963年 -配偶者 ダイアン・アボット(1976年 - 1988年)グレイス・ハイタワー(1997年 - )主な作品 『ミーン・ストリート』(1973年)...

Interdisciplinary study An infrared spectrometer, which can be used for the analysis of cultural heritage materials.With respect to cultural property, conservation science is the interdisciplinary study of the conservation of art, architecture, technical art history and other cultural works through the use of scientific inquiry. General areas of research include the technology and structure of artistic and historic works. In other words, the materials and techniques from which cultural, artis...

1981 book by Karen Wynn Fonstad The Atlas of Middle-earth Dust wrapper, first editionAuthorKaren Wynn FonstadIllustratorKaren Wynn FonstadCover artistAlan Lee (Second edition)CountryUnited StatesSubjectMiddle-earthGenreAtlasPublisherHoughton MifflinPublication date1981Media typeHardcoverPages190 (210 with notes)ISBN0-395-53516-6OCLC24142309Dewey Decimal823/.912 20LC ClassG3122.M5 F6 1991 The Atlas of Middle-earth by Karen Wynn Fonstad is an atlas of J. R. R. Tolkien's fictiona...

「俄亥俄」重定向至此。关于其他用法,请见「俄亥俄 (消歧义)」。 俄亥俄州 美國联邦州State of Ohio 州旗州徽綽號:七葉果之州地图中高亮部分为俄亥俄州坐标:38°27'N-41°58'N, 80°32'W-84°49'W国家 美國加入聯邦1803年3月1日,在1953年8月7日追溯頒定(第17个加入联邦)首府哥倫布(及最大城市)政府 • 州长(英语:List of Governors of {{{Name}}}]]) •&...

إمام المسلمين و أمير المؤمنين عبد الله بن سعود آل سعود ( الإمام الذي افتدى شعبه ) إمام الدولة السعودية الأولى الرابع الحاكم الخامس من آل سعود أمير إمارة الدرعية الثامن عشر صورة في كتاب تاريخ مصر في ظل حكومة محمد علي (1823) الصادر عن فيلكس مانجان إمام الدولة السعودية الأولى في ا...

国民阵线Barisan NasionalNational Frontباريسن ناسيونلபாரிசான் நேசனல்国民阵线标志简称国阵,BN主席阿末扎希总秘书赞比里署理主席莫哈末哈山总财政希山慕丁副主席魏家祥维纳斯瓦兰佐瑟古律创始人阿都拉萨成立1973年1月1日 (1973-01-01)[1]设立1974年7月1日 (1974-07-01)前身 联盟总部 马来西亚 吉隆坡 50480 秋傑区敦依斯迈路太子世贸中心(英�...

Докладніше: Втрати силових структур внаслідок російського вторгнення в Україну У статті наведено список втрат українських військовослужбовців у російсько-українській війні, починаючи з 1 червня 2022 року по 15 червня 2022 року (включно). Втрати з українського боку публіку�...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

У этого термина существуют и другие значения, см. Страна (значения). СтранаТелеканал «Страна» Страна Россия Зона вещания Россия Время вещания круглосуточно Язык вещания русский Штаб-квартира Москва, 5-я улица Ямского Поля, 9 Формат изображения 576i (SDTV) Дата начала вещ...

Style of human-computer interaction Not to be confused with WIMP (software bundle) or WIMP (Physics).A word processing program that uses a WIMP paradigm, providing mouse-operated toolbars and menus to access its functions In human–computer interaction, WIMP stands for windows, icons, menus, pointer,[1][2][3] denoting a style of interaction using these elements of the user interface. Other expansions are sometimes used, such as substituting mouse and mice for menus, o...
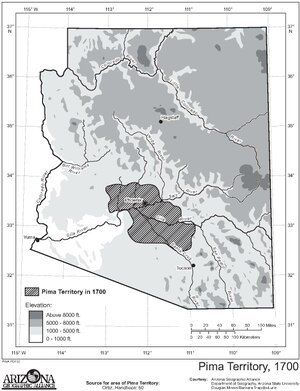
Indigenous tribe in the US and Mexico Ethnic group Akimel O'odhamPimaO'odham portraitsTotal population19,921 ± 4,574 (2010)[1]Regions with significant populations United States ( Arizona)LanguagesO'odham, English, SpanishReligionRoman Catholicism, traditional tribal religion[2]Related ethnic groups Ak-Chin O'odham Hia C-ed O'odham Tohono O'odham The Akimel O'odham (O'odham for river people), also called the Pima, are a group of Native Americans living in an area consisting of...

Sodium ferrioxalate Names IUPAC name Sodium iron(III) oxalate, sodium oxalatoferrate, sodium trisoxalatoferrate Other names Sodium ferrioxalate Sodium ferric oxalate Sodium trisoxalatoferrate (III) Sodium oxalatoferrate Identifiers CAS Number 5936-14-1 Y555-34-0 3D model (JSmol) Interactive image ChemSpider 147755 ECHA InfoCard 100.008.267 EC Number 209-092-9 PubChem CID 131855679 CompTox Dashboard (EPA) DTXSID60890505 InChI InChI=1S/3C2H2O4.Fe.3Na/c3*3-1(4)2(5)6;;;;/h3*(H,3,4)(H,5,6);;...

Запрос «шинок» перенаправляется сюда; см. также другие значения. Запрос «Корчмарь» перенаправляется сюда; о нарушителе закона см. Корчемник. Эту страницу предлагается объединить со страницей Кабак.Пояснение причин и обсуждение — на странице Википедия:К объединени�...

1868–1869 Japanese civil war Boshin War戊辰戦争Part of the Meiji RestorationThe Battle of Ueno, Yoshimori Utagawa, 1869DateJanuary 27, 1868 – June 27, 1869(1 year and 5 months)LocationJapanResult Imperial victory End of the shogunate Restoration of imperial ruleBelligerents 1868 Imperial Court Tozama: Satsuma Domain Chōshū Domain Other tozama daimyōs: Tosa Domain Hiroshima Domain Tsu Domain Kubota Domain Saga Domain Ōg...

German army division during World War II Not to be confused with 2nd SS Panzer Division Das Reich or 2nd Panzergrenadier Division (Bundeswehr). 2nd Panzer Division2. Panzer-DivisionUnit insigniaActive15 October 1935 – 8 May 1945Country Nazi GermanyBranch German ArmyTypePanzerRoleArmoured warfareSizeDivisionGarrison/HQWehrkreis XIII: Würzburg (1935–38)Wehrkreis XVIII: Vienna (1938–45)EngagementsWorld War II Invasion of Poland Battle of France Battle of Greece Operation Barbaro...
