Решето Аткина
|
Read other articles:

CachanNegaraPrancisArondisemenL'Haÿ-les-RosesAntarkomuneCommunautéd'agglomérationde Val de Bièvre Cachan merupakan sebuah komune di pinggiran selatan Paris, Prancis. Terletak 6.7 km (4.2 mil) dari pusat kota Paris. École Normale Supérieure de Cachan terletak di sini. Nama Pada Abad Pertengahan, Cachan tercantum dalam teks Latin Pertengahan sebagai Caticantum, kemudian berubah menjadi Cachentum, Cachant, dan kemudian Cachan. Beberapa orang mengetahui Caticantum berarti nyanyian kuci...

Mr.Abdulmadjid Djojohadiningrat ꦄꦧ꧀ꦢꦸꦭ꧀ꦩꦗꦶꦢ꧀ꦗꦺꦴꦪꦺꦴꦮꦢꦶꦤꦶꦤꦔꦿꦠ꧀ Wali Kota Semarang ke-4Masa jabatan7 Januari 1958 – 1 Januari 1960PresidenSoekarno PendahuluHadisoebeno SosrowerdojoPenggantiSoebagyono TjondrokoesoemoMenteri Muda Dalam Negeri Indonesia ke-3Masa jabatan3 Juli 1947 – 29 Januari 1948PresidenSoekarnoPerdana MenteriAmir Sjarifoeddin PendahuluWijonoPenggantiTidak ada; jabatan dihapuskanWakil Menteri...

Ilustrasi yang menunjukkan perbedaan hiperplasi dan hipertrofi Hiperplasi adalah peristiwa meningkatnya jumlah sel yang terjadi pada organ tertentu akibat peningkatan proses mitosis.[1] Mekanisme Hiperplasi dapat terjadi dan ditemui pada sel yang dirangsang dengan peningkatan beban kerja, pensinyalan oleh hormon, atau sinyal yang dihasilkan secara lokal sebagai respon terhadap penurunan kepadatan jaringan.[1] Hiperplasi hanya dapat terjadi pada sel-sel yang mengalami proses mi...

جناح البحث والتحليل الهندي (بالإنجليزية: Research and Analysis Wing)[1] جناح البحث والتحليل الهندي تفاصيل الوكالة الحكومية البلد الهند مؤسس أنديرا غاندي تأسست 21 سبتمبر 1968 المركز نيودلهي28°35′19″N 77°14′16″E / 28.588611111111°N 77.237861111111°E / 28.588611111111; 77.237861111111 ا�...

Street in Boston, Massachusetts, US Congress StreetCongress Street from Dock Square, Boston, 2010West endSudbury Street / Merrimac StreetMajorjunctionsState StreetMilk StreetFranklin Street I-93 (Atlantic Ave./Purchase St.)Dorchester AvenueEast endNorthern Avenue Congress Street in Boston, Massachusetts, is located in the Financial District and South Boston. It was first named in 1800. It was extended in 1854 (from State Street) as far as Atlantic Avenue, and in 1874 across Fort Poi...

American politician (born 1984) Joe NeguseHouse Assistant Democratic LeaderIncumbentAssumed office March 20, 2024LeaderHakeem JeffriesPreceded byJim ClyburnChair of the House Democratic Policy and Communications CommitteeIn officeJanuary 3, 2021 – March 20, 2024LeaderNancy PelosiHakeem JeffriesPreceded byDavid CicillineSucceeded byDebbie DingellMember of the U.S. House of Representativesfrom Colorado's 2nd districtIncumbentAssumed office January 3, 2019Preceded ...

Muhammad Ridho Djazulie M. Ridho (kiri) dan Awan Setho bersama Indonesia pada tahun 2018Informasi pribadiNama lengkap Muhammad Ridho DjazulieTanggal lahir 21 Agustus 1992 (umur 31)Tempat lahir Pekalongan, IndonesiaTinggi 179 m (587 ft 3 in)Posisi bermain penjaga gawangInformasi klubKlub saat ini Bali UnitedNomor 88Karier senior*Tahun Tim Tampil (Gol)2010–2015 Persip Pekalongan 50 (0)2012–2013 → Persekabpur Purworejo (loan) 15 (0)2015–2017 PS Bangka 28 (0)2017–20...

English rail transport magazine Today's Railways UKEditorRobert PritchardFormer editorsPeter FoxPaul AbellJonathan WebbStaff writersAlan YearsleyIan BeardsleyCategoriesRail transportFrequencyMonthlyPublisherPlatform 5FounderPlatform 5First issueJanuary 2002CountryEnglandBased inSheffieldLanguageEnglishWebsitewww.platform5.comISSN1475-9713 Today's Railways UK is an English-based monthly magazine covering rail transport in Great Britain. It was founded by Platform 5 in January 2002 as Entra...

Indonesian Television Awards 2020Logo Indonesian Television AwardsTanggal25 September 2020 (2020-09-25)LokasiStudio RCTI+Jakarta BaratNegara IndonesiaPembawa acaraRaffi AhmadAyu DewiAndre TaulanyPenampilanPUBLICSuperMChoi SiwonAgnez MoRhoma IramaLyodra GintingTiara AndiniZiva MagnolyaBetrand Peto Putra OnsuSitus webwww.indonesiantvawards.comSiaran televisi/radioSaluranRCTIMNCTV← 2019 Indonesian Television Awards2021 → Indonesian Television Awards 2020 adalah penghargaan ...

Chemical compound α-PyrrolidinoheptaphenoneClinical dataOther namesα-PHPP; alpha-PHPP; alpha-Pyrrolidinoheptiophenone; alpha-Pyrrolidinoheptanophenone; PV-8; PV8; Aphpp; A-PHPPLegal statusLegal status CA: Schedule I DE: NpSG (Industrial and scientific use only) UK: Class B US: Schedule I Identifiers IUPAC name 1-Phenyl-2-pyrrolidin-1-ylheptan-1-one CAS Number13415-83-3 13415-55-9 (HCl)2304915-38-4 (R)2304915-72-6 (S)PubChem CID69245534ChemSpider57379805UNIIE6220IS097Chem...

هنودمعلومات عامةنسبة التسمية الهند التعداد الكليالتعداد قرابة 1.21 مليار[1][2]تعداد الهند عام 2011ق. 1.32 مليار[3]تقديرات عام 2017ق. 30.8 مليون[4]مناطق الوجود المميزةبلد الأصل الهند البلد الهند الهند نيبال 4,000,000[5] الولايات المتحدة 3,982,398[6] الإمار...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2016) This list divides the world using the seven-continent model, with islands grouped into adjacent continents. The continents are: إفريقيا آسيا أوروبا أمريكا الشمالية ...
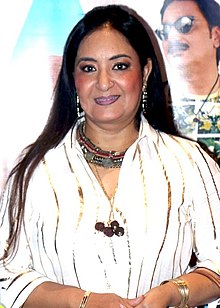
Indian singer Dr. Jaspinder NarulaNarula at the special screening of Mr. KabaadiBackground informationBorn (1970-11-14) 14 November 1970 (age 53)GenresPunjabi music, religious music, Bollywood musicOccupation(s)Playback singerInstrument(s)VocalsYears active1994–2014Musical artist Jaspinder Narula (born 14 November 1970) is an Indian singer of playback, classical and Sufi music. She is known for her work in Hindi and Punjabi cinema. She shot to fame after the duet Pyaar To Hona Hi Tha w...

本表是動態列表,或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源,曾潛伏於中華民國國軍、被中國共產黨聲稱或承認,或者遭中華民國政府調查審判,為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準,正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

Part of the 2004 U.S. presidential election This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (March 2019) (Learn how and when to remove this message) 2004 United States presidential debates ← 2000 September 30, and October 8 and 13, 2004 2008 → Nominee George W. Bush John Kerry Party Republican Democratic Home state Texas Massa...

Overview of tourism in Gujarat, India This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documen...

This article is about One Piece chapters 1016 to now. For a guide, see lists of One Piece chapters. Volume 101 of One Piece, released in Japan by Shueisha on December 3, 2021 One Piece is a Japanese manga series written and illustrated by Eiichiro Oda which has been translated into various languages and spawned a substantial media franchise, including animated and live action television series, films, video games, and associated music and merchandise. It follows the adventures of the teenage...

Armoiries de la municipalité de Frederiksberg. La municipalité de Frederiksberg est une commune du Danemark de 104 305 habitants au 1er janvier 2020. Elle est totalement incluse dans la communauté urbaine de Copenhague. Elle est constituée de neuf paroisses dont celle de Frederiksberg où siège le conseil municipal. Histoire La commune de Frederiksberg constitue à la fois un quartier de Copenhague et une municipalité à part entière. Initialement Frederiksberg se trouvait à l'extéri...

Finding Mr. DestinySutradaraJang Yoo-jeongProduserMin Jin-sooMin Kyu-dongDitulis olehLee Kyung-uiBerdasarkanFinding Kim Jong-wook (musikal)PemeranIm Soo-jungGong YooPenata musikPark Ji-woongSinematograferLee Hyung-dukPenyuntingKim Hyeong-juDistributorCJ EntertainmentTanggal rilis 9 Desember 2010 (2010-12-09) Durasi112 menitNegaraKorea SelatanBahasaKoreaPendapatankotor$7,444,073[1] Finding Mr. Destiny (Hangul: 김종욱 찾기; RR: Kim Jong-uk chat-gi&#...

高壁الأعرافAl-A'rafアル・アアラーフ 高壁啓示 マッカ啓示章題の意味 第46節にある真理の正しい道に立つ高い壁[1]詳細スーラ 第7章アーヤ 全206節ジュズウ 8 - 9番ヒズブ 16 - 18番ルクー 24回サジダ節 1回(第206節)神秘文字 المص前スーラ 家畜次スーラ 戦利品テンプレートを表示 『高壁』とは、クルアーンにおける第7番目の章(スーラ)。206の節(アーヤ)から�...







