Полугруппа
|
Read other articles:

Keuskupan Agung TuguegaraoArchidiœcesis Tuguegaraoana Arkidiocesis ti Tuguegarao (Ilocano) Arkidiocesis nat Tuguegarao (Ibanag) Archidiocensya yoh Tuguegaraow (Malaweg) Arquidiócesis de Tuguegarao (Spanyol) Katolik Roma Katedral TuguegaraoLambang Keuskupan Agung TuguegaraoLokasiNegaraFilipinaWilayahLembah CagayanProvinsi gerejawiTuguegaraoStatistikLuas9.000 km2 (3.500 sq mi)Populasi- Total- Katolik(per 2010)1.709.0001,356,000 (79.3%)InformasiDenominasiKato...
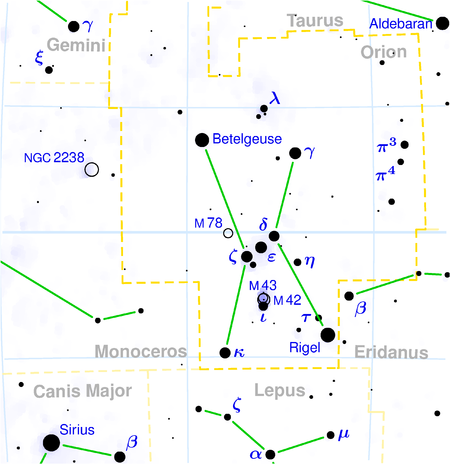
Pi3 Orionis The location of Pi3 Orionis (π3) in the constellation of Orion. Data pengamatan Epos J2000.0 Ekuinoks J2000.0 Rasi bintang Orion Asensio rekta 04j 49m 50.4d Deklinasi +06° 57′ 41″ Magnitudo tampak (V) 3.60 Ciri-ciri Kelas spektrum F6V Indeks warna U−B -0.01 Indeks warna B−V 0.45 Jenis variabel Suspected AstrometriKecepatan radial (Rv)24.3 km/sGerak diri (μ) RA: 463.44 ...

Disambiguazione – Se stai cercando il movimento guerrigliero della Colombia, vedi Esercito Popolare di Liberazione (Colombia). Disambiguazione – Se stai cercando l'esercito della Repubblica di Cina (Taiwan), vedi Zhōnghuá Mínguó Lùjūn. Questa voce o sezione sull'argomento guerra è ritenuta da controllare. Motivo: La voce è piena di dati non aggiornati e senza un minimo riscontro con fonte oltre che pareri e affermazioni personali Partecipa alla discussione e/o correggi la vo...

Državno prvenstvo 1923 Competizione Državno prvenstvo Sport Calcio Edizione 1ª Organizzatore FSJ Date dal 2 settembre 1923al 1º ottobre 1923 Luogo Regno dei Serbi, Croati e Sloveni Partecipanti 6 Formula Eliminazione diretta Risultati Vincitore Građanski Zagabria(1º titolo) Statistiche Miglior marcatore Dragan Jovanović (4) Incontri disputati 6 Gol segnati 28 (4,67 per incontro) Pubblico 26 000 (4 333 per incontro) Građanski Zagabria 1923 Cronologia della ...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Terrier – berita · surat kabar · buku · cendekiawan · JSTOR Anjing terrier tahun 1875 (jenis English Toy Terrier) Seekor terrier adalah anjing yang berasal dari satu di antara berbagai ras atau ras darat jeni...

The qualification for 2004 Men's Olympic Volleyball Tournament was held from 7 September 2003 to 30 May 2004. Means of qualification Qualified for the 2004 Summer Olympics Qualified for the 2004 World Olympic Qualification Tournaments Host country FIVB reserved a vacancy for the 2004 Summer Olympics host country to participate in the tournament. Greece 2003 World Cup Main article: 2003 FIVB Volleyball Men's World Cup Venues: Japan Dates: 16–29 November 2003 The top three teams ...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Leander-Class cruiser For other ships with the same name, see HMS Orion. HMS Orion History United Kingdom NameHMS Orion BuilderDevonport Dockyard / Vickers Armstrong, Barrow-in-Furness Laid down26 September 1931 Launched24 November 1932 Commissioned18 January 1934 Decommissioned1947 IdentificationPennant number: 85 FateSold for scrap 19 July 1949 General characteristics Class and typeLeander-class light cruiser Displacement 7,270 tons standard 9,740 tons full load Length554.9 ft (169.1&#...

Swedish Football 1926–27 Allsvenskan (Tier 1) Division 2 (Tier 2) Division 3 (Tier 3) The 1926-27 season in Swedish football, starting August 1926 and ending July 1927: Honours Official titles Title Team Reason 1926–27 Swedish Champions[1] None – Competitions Level Competition Team 1st level Allsvenskan 1926–27 GAIS 2nd level Division 2 Uppsvenska Serien 1926–27 Sandvikens IF Division 2 Mellansvenska Serien 1926–27 IK City Division 2 Östsvenska Serien ...

La taille et la puissance des cuirassés augmentèrent rapidement, avant, pendant et après la Première Guerre mondiale, résultats de la compétition dans le domaine de la construction navale entre grandes puissances, au rang desquelles se trouvaient la Grande-Bretagne et l'Allemagne. Elle prit fin avec les traités de Versailles et de Washington. La course germano-britannique aux armements navals désigne la rivalité qui opposa l'Empire allemand et le Royaume-Uni pour s'assurer la suprém...

Lempira Departamento Localización del departamento de LempiraCoordenadas 14°35′20″N 88°34′53″O / 14.588955555556, -88.581355555556Capital Gracias • Población 57 182 habitantesEntidad Departamento • País HondurasGobernador José Enamorado(2022-2026)Subdivisiones 28 municipiosEventos históricos • Fundación 1825Superficie Puesto 11.º de 18 • Total 4,228 km²Clima Tropical seco AwTemplado subhúmedo CwbPoblación (...

American politician Curt Meier30th Treasurer of WyomingIncumbentAssumed office January 7, 2019GovernorMark GordonPreceded byMark GordonMember of the Wyoming Senatefrom the 3rd districtIn officeJanuary 1995 – January 8, 2019Preceded byJim GeringerSucceeded byCheri Steinmetz Personal detailsBorn (1953-01-01) January 1, 1953 (age 71)La Grange, Wyoming, U.S.Political partyRepublicanSpouseCharleneEducationUniversity of Wyoming (BS) Curt Meier (born January 1, 1953) is an Americ...

Untuk penulis olahraga, lihat Red Foley (penulis olahraga). Red FoleyInformasi latar belakangNama lahirClyde Julian FoleyNama lainMr. Country MusicLahir(1910-06-17)17 Juni 1910AsalBlue Lick, Kentucky, ASMeninggal19 September 1968(1968-09-19) (umur 58)Fort Wayne, Indiana, ASGenreCountrygospelrockabillyboogierhythm and bluesPekerjaanpenyanyi-penulis lagu, musisi, pembawa acara TV dan radio, aktorInstrumengitar, banjoTahun aktif1930–1968LabelConqueror, Melotone, DeccaArtis terkaitThe Cumb...

Polish football club Football clubHetman ZamośćFull nameK.S. Hetman ZamośćNickname(s)Hetman Wielki KoronnyFounded14 April 1934; 90 years ago (1934-04-14)GroundStadion OSiR w ZamościuCapacity12,500ChairmanKrzysztof RysakCoachRobert WieczerzakLeagueIV liga Lublin2023–24Regional league Zamość, 1st of 16 (promoted)WebsiteClub website Home colours Away colours Hetman Zamość is a football club based in Zamość, Poland. The club plays in the IV liga Lublin, which is the...

US cargo ship class of WWII This article is about the class of US cargo ship. For ships named Liberty, see Liberty (ship). SS John W. Brown, one of four surviving Liberty ships, photographed in 2000 Class overview NameLiberty ship Builders18 shipyards in the United States CostUS$2 million ($43 million in 2024) per ship[1] Planned2,751 Completed2,710 Active2 (Traveling museum ships) Preserved4 General characteristics Class and typeCargo ship Tonnage7,176 GRT, 10,865...

Sedeinga pyramidsNapatan-Meroic Necropolis of SedeingaSedeingaShown within Northeast AfricaShow map of Northeast AfricaSedeingaSedeinga (Sudan)Show map of SudanLocationNorthern State, SudanRegionNubiaCoordinates20°33′11.92″N 30°17′27.48″E / 20.5533111°N 30.2909667°E / 20.5533111; 30.2909667TypeSettlementSite notesConditionrestored Temple of Queen Tiyi at Sedeinga Chalice from Sedeinga, National Museum of Sudan, Khartoum, Sudan The Sedeinga pyramids are a gr...

Aviation term for a corkscrew downward path Tailspin redirects here. For other uses, see Tailspin (disambiguation). Not to be confused with the Disney animated TV series TaleSpin. Spin — an aggravated stall and autorotation In flight dynamics a spin is a special category of stall resulting in autorotation (uncommanded roll) about the aircraft's longitudinal axis and a shallow, rotating, downward path approximately centred on a vertical axis.[1] Spins can be entered intentionally or ...

Protection of wilderness areas in the U.S. The Wilderness Act protects exceptionally undisturbed natural areas and scenery, such as in the Ansel Adams Wilderness. The National Wilderness Preservation System (NWPS) of the United States protects federally managed wilderness areas designated for preservation in their natural condition. Activity on formally designated wilderness areas is coordinated by the National Wilderness Preservation System. Wilderness areas are managed by four federal land ...

Questa voce o sezione sull'argomento competizioni ciclistiche non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Campionati del mondo di ciclismo su stradaSport Ciclismo su strada TipoGare individuali CategoriaCampionato del mondo FederazioneUnione Ciclistica Internazionale PaeseVariabile OrganizzatoreUnione...

Voce principale: Fußball-Bundesliga (Austria). Quello che segue è l'elenco dei vincitori del campionato austriaco di calcio: Indice 1 Albo d'oro 1.1 Titoli ufficiali 1.1.1 1. Klasse (Niederösterreichischer Fussballverband) 1.1.2 I. Liga (Wiener Fußball-Verband) 1.1.3 Nationalliga (Wiener Fußball-Verband) 1.1.4 Gauliga XVII (Nationalsozialistischer Reichsbund für Leibesübungen) 1.1.5 1. Klasse (Wiener Fußball-Verband) 1.1.6 Staatsliga (Österreichische Fußball-Staatsliga) 1.1.7 Natio...





















































