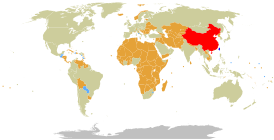
Политика одного Китая

Политика одного Китая
 Китайская Народная Республика (КНР) Китайская Республика (КР) Страны, признающие только КНР Страны, признающие только Китайскую Республику Страны, признающие КНР и имеющие неофициальные отношения с КР Китайская Народная Республика (КНР) Китайская Республика (КР) Страны, признающие только КНР Страны, признающие только Китайскую Республику Страны, признающие КНР и имеющие неофициальные отношения с КР

Политика одного Китая — принцип внешней политики государств, в основе которого лежит признание существования на карте мира только одного китайского государства, несмотря на то, что существует два государства, претендующих на название «Китай»: Китайская Народная Республика (материковая часть Китая) и Китайская Республика (остров Тайвань). Государства, признающие Китайскую Народную Республику, не признают Китайскую Республику и наоборот. Признавая одно государство, государство разрывает дипломатические отношения с другим.

Политика одного Китая также отличается от принципа единого Китая («политики единого Китая»), на котором настаивают Китайская Народная Республика и Китайская Республика, которые считают друг друга частью «единого Китая». Модифицированная форма принципа единого Китая, отраженная в консенсусе 1992 года, является неотъемлемой частью внешней политики Китайской Народной Республики и Китайской Республики, по которой обе страны признают материковый Китай и Тайвань частью единого Китая, но при этом каждая сторона по-своему интерпретирует принцип и считает себя единственным легитимным правительством Китая, признавая возможность диалога между сторонами.

Принцип единого Китая подвергается критике со стороны сторонников движения за независимость Тайваня, который настаивает на провозглашении «Республики Тайвань» и развития отдельной от материкового Китая идентичности через «тайванизацию». Влияние этого движения на правительство РК вызывает политическую нестабильность: после того, как в 1949 году Коммунистическая партия Китая вытеснила РК из материкового Китая в ходе китайской гражданской войны и основала КНР, националистическое правительство Китайской Республики, которая закрепилась на Тайване, продолжало утверждать, что оно является единственным легитимным правительством Китая. В период президентства Ли Дэнхуэя в конституцию РК были включены дополнительные статьи, согласно которым к объединению государства эта конституция может применяться только на территории Тайваня[1]. Однако избранный в 2008 году президент КР Ма Инцзю 8 октября 2008 года вновь подтвердил претензии на материковую часть Китая.

Примечания

  1. ↑ Lee Teng-hui 1999 interview with Deutsche Welle: https://fas.org/news/taiwan/1999/0709.htm Архивная копия от 9 апреля 2015 на Wayback Machine

Ссылки

Read other articles:

Helse

Helse Lambang kebesaranLetak Helse di Dithmarschen NegaraJermanNegara bagianSchleswig-HolsteinKreisDithmarschen Municipal assoc.Marne-NordseeSubdivisions9Pemerintahan • MayorHans-Hermann Meier (SPD)Luas • Total11,44 km2 (442 sq mi)Ketinggian4 m (13 ft)Populasi (2013-12-31)[1] • Total865 • Kepadatan0,76/km2 (2,0/sq mi)Zona waktuWET/WMPET (UTC+1/+2)Kode pos25709Kode area telepon04851Pelat kendaraanHEISitu...

 

Herbarium Hortus Botanicus Bogoriensis

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Herbarium Hortus Botanicus Bogoriensis adalah salah satu herbarium yang ada di Kota Bogor. Fungsi herbarium ini adalah sebagai tempat penelitian, pendidikan dan determinasi tumbuhan yang dikoleksi oleh Kebun Raya Bogor. Herbarium Hortus Botanicus Bogor...

 

Kevin Foley

Kevin Foley Foley pada tahun 2010Informasi pribadiNama lengkap Kevin Patrick FoleyTanggal lahir 1 November 1984 (umur 39)Tempat lahir Luton, InggrisTinggi 1,83 m (6 ft 0 in)[1]Posisi bermain BekInformasi klubKlub saat ini CopenhagenNomor 16Karier junior1995–2002 Luton TownKarier senior*Tahun Tim Tampil (Gol)2002–2007 Luton Town 151 (3)2007–2015 Wolverhampton Wanderers 194 (5)2014 → Blackpool (loan) 5 (0)2014–2015 → Blackpool (loan) 4 (0)2015– Copenha...

Pekan Mode New York

Peragawati Milagros Schmoll dalam Pekan Mode New York 2009. Pekan Mode New York adalah pagelaran pekan mode yang diselenggarakan pada bulan Februari dan September setiap tahunnya di New York City, Amerika Serikat. Pekan mode ini adalah salah satu dari empat besar pekan mode yang diselenggarakan di seluruh dunia (bersama dengan Paris, London, dan Milan.[1][2] Sejarah Pekan Mode New York (yang awalnya disebut Press Week) adalah pekan mode yang pertama kali diselenggarakan di dun...

 

Execution by elephant

Execution method from Asia Illustration from the Akbarnama, the official chronicle of the reign of Akbar, the third Mughal emperor Execution by elephant was a method of capital punishment in South and Southeast Asia, particularly in India, where Asian elephants were used to crush, dismember, or torture captives during public executions. The animals were trained to kill victims immediately or to torture them slowly over a prolonged period. Most commonly employed by royalty, the elephants were ...

 

Condor (APC)

Condor APC Sebuah Condor milik Tentara Malaysia Jenis Armoured personnel carrier Negara asal Germany Malaysia Spesifikasi Berat 12.4 metric tons[1]|length=6.13 m[1] Panjang 6.13 m[1] Lebar 2.47 m[1] Tinggi 2.18 m[1] Awak 2+12 Senjatautama 20 mm cannon Senjatapelengkap 7.62 mm Jenis Mesin Mercedes Benz OM352A / 6 cylinder diesel engine[1]168 hp (125 kW) Suspensi Portal axle with coil spring and shock-absorbers[1] Daya jela...

National Council for Promotion of Urdu Language

National Council for Promotion of Urdu LanguageAgency overviewFormed1 April 1996; 28 years ago (1 April 1996)JurisdictionGovernment of IndiaHeadquartersDelhi, IndiaAgency executiveShri Dharmendra PradhanProf. Aquil AhmadWebsiteurducouncil.nic.in The National Council for Promotion of Urdu Language (Urdu: قومی کونسل برائے فروغ اردو زبان, Qaumī Kaunsil barā-yi Farōg̱ẖ-i Urdū Zabān NCPUL) is an autonomous regulatory body in the Government ...

 

K. L. Mohana Varma

K.L. MohanavarmaBorn (1936-07-08) 8 July 1936 (age 87)Cherthala, Alappuzha District, Kerala State, IndiaOccupationNovelist, short story writerLanguageMalayalam, EnglishGenreNovel, short story, children's literature, travelogue, essaysSubjectSports, historyLiterary movementRealismNotable worksCricket, Ohari, NeethiNotable awardsSahitya Akademi Award, Kerala Sahitya Akademi AwardSpouseRadha Varma K. L. Mohana Varma (born 1936) is a Malayalam–language novelist, short story writer and jou...

 

Памятник Фёдору Коню

ПамятникПамятник Фёдору Коню 54°46′46″ с. ш. 32°02′37″ в. д.HGЯO Страна  Россия Город Смоленск Скульптор О. Н. Комов Архитектор А. К. Анипко Дата основания 1991 Строительство 1991 Статус  ОКН № 6702680000№ 6702680000  Медиафайлы на Викискладе Памятник Фёдору Коню — одна �...

莎拉·阿什頓-西里洛

莎拉·阿什頓-西里洛2023年8月，阿什頓-西里洛穿著軍服出生 (1977-07-09) 1977年7月9日（46歲） 美國佛羅里達州国籍 美國别名莎拉·阿什頓（Sarah Ashton）莎拉·西里洛（Sarah Cirillo）金髮女郎（Blonde）职业記者、活動家、政治活動家和候選人、軍醫活跃时期2020年—雇主內華達州共和黨候選人（2020年）《Political.tips》（2020年—）《LGBTQ國度》（2022年3月—2022年10月）烏克蘭媒�...

 

Haro, La Rioja

Festival anggur di Haro Reruntuhan puri Haro (pengucapan bahasa Spanyol: [ˈaɾo]) merupakan nama dari sebuah kota dan munisipalitas yang terletak di barat laut provinsi La Rioja, Spanyol utara. Wilayah ini menghasilkan minuman anggur dan mengadakan Festival Anggur Haro setiap tahunnya. Lihat pula Wangsa Haro Tempranillo Referensi Pranala luar Wikimedia Commons memiliki media mengenai Haro (La Rioja). Ayuntamiento de Haro Koordinat: 42°35′N 2°51′W / 42.583°N 2.850�...

 

2D Z-transform

The 2D Z-transform, similar to the Z-transform, is used in multidimensional signal processing to relate a two-dimensional discrete-time signal to the complex frequency domain in which the 2D surface in 4D space that the Fourier transform lies on is known as the unit surface or unit bicircle.[1] The 2D Z-transform is defined by X z ( z 1 , z 2 ) = ∑ n 1 = 0 ∞ ∑ n 2 = 0 ∞ x ( n 1 , n 2 ) z 1 − n 1 z 2 − n 2 {\displaystyle X_{z}(z_{1},z_{2})=\sum...

25I-NBF

Chemical compound 25I-NBFClinical dataATC codenoneLegal statusLegal status BR: Class F2 (Prohibited psychotropics)[1] DE: NpSG (Industrial and scientific use only) UK: Class A Identifiers IUPAC name 2-(4-iodo-2,5-dimethoxyphenyl)-N-[(2-fluorophenyl)methyl]ethan-1-amine CAS Number919797-21-0 YPubChem CID57469209ChemSpider24751866 YUNIIMR8FRH5W3CCompTox Dashboard (EPA)DTXSID00726753 Chemical and physical dataFormulaC17H19FINO2Molar mass415.247 g·mol−13D ...

 

2018 World Rowing Championships – Men's coxless pair

Men's coxless pair at the 2018 World Rowing ChampionshipsVenuePlovdiv Regatta VenueLocationPlovdiv, BulgariaDates9–15 SeptemberCompetitors51 from 25 nationsWinning time6:14.96Medalists  Martin SinkovićValent Sinković   Croatia Marius CozmiucCiprian Tudosă   Romania Valentin OnfroyThéophile Onfroy   France← 20172019 → 2018 World Rowing ChampionshipsOpenweight eventsSingle scullsmenwomenDouble scu...

 

العلاقات الجنوب إفريقية الميانمارية

العلاقات الجنوب أفريقية الميانمارية جنوب أفريقيا ميانمار   جنوب أفريقيا   ميانمار تعديل مصدري - تعديل   العلاقات الجنوب أفريقية الميانمارية هي العلاقات الثنائية التي تجمع بين جنوب أفريقيا وميانمار.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة ...

Вигдорова, Фрида Абрамовна

В Википедии есть статьи о других людях с фамилией Вигдоров. Фрида Абрамовна Вигдорова Дата рождения 3 (16) марта 1915[1] Место рождения Орша, Оршанский уезд, Могилёвская губерния, Российская империя Дата смерти 7 августа 1965(1965-08-07)[2][1] (50 лет) Место смерти Москва, ССС�...

 

Ambiani

Belgic tribe Ambiani hemi stater. Stylized head. The Ambiani (Gaulish: Ambiāni, 'those around') were a Belgic coastal tribe dwelling in the modern Picardy region during the Iron Age and Roman periods. They settled in the region between the 4th century and the second part of the 2nd century BC. In 113–101 BC, they took part in the fights against the Cimbri and Teutoni invaders during the Cimbrian War. In 57 and 52 BC, they participated in Gallic coalitions against Caesar, before their event...

 

Walter Wolf Racing

Walter Wolf Racing Caractéristiques Caractéristiques de l'écurie Discipline Formule 1 Localisation Reading, Royaume-Uni Dirigeants et pilotes Président Walter Wolf Directeur technique Harvey Postlethwaite Pilotes Jody Scheckter Bobby Rahal Keke Rosberg James Hunt Caractéristiques techniques Châssis Wolf Moteurs Ford-Cosworth Pneumatiques Goodyear Résultats Début Grand Prix d'Argentine 1977 Dernière course Grand Prix des États-Unis Est 1979 Courses disputées 48 Points marqués 79 T...

Bottini di Siena

Questa voce o sezione sugli argomenti Toscana e ingegneria non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti dei progetti di riferimento 1, 2. I bottini di Siena sono le gallerie sotterranee costruite nel XIII-XV secolo per l'approvvigionamento idrico. Indice 1 Descrizione 2 Storia 3 Devozione 4 Leggende 4.1 Omiccioli e fuggisoli 4.2 I...

 

Self-organized criticality

Concept in physics An image of the 2d Bak-Tang-Wiesenfeld sandpile, the original model of self-organized criticality. Complex systems Topics Self-organizationEmergence Collective behaviorSocial dynamics Collective intelligence Collective action Self-organized criticality Herd mentality Phase transition Agent-based modelling Synchronization Ant colony optimization Particle swarm optimization Swarm behaviour Collective consciousness NetworksScale-free networks Social network analysis Small-worl...