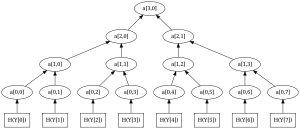
Подпись Лэмпорта
|
Read other articles:

Bandar Udara Internasional FaleoloIATA: APWICAO: NSFA APWLokasi bandar udara di SamoaInformasiJenisPublikMelayaniApia, Pulau Upolu, SamoaKetinggian dpl18 mdplKoordinat13°49′47″S 172°00′30″W / 13.82972°S 172.00833°W / -13.82972; -172.00833Landasan pacu Arah Panjang Permukaan m kaki 08/26 3.000 9,843 Aspal Sumber: DAFIF[1][2] Bandar Udara Internasional Faleolo (IATA: APW, ICAO: NSFA) adalah bandar udara yang berlokasi sekitar 40...

Ikan Genghis Khan Status konservasi Kritis (IUCN 3.1)[1] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Actinopterygii Subkelas: Neopterygii Infrakelas: Teleostei Superordo: Ostariophysi Ordo: Siluriformes Famili: Pangasiidae Genus: Pangasius Spesies: P. sanitwongsei Nama binomial Pangasius sanitwongseiSmith, 1931 Sinonim Pangasius beani Smith, 1931 Pangasius sanitwangsei Smith, 1931 Ikan Genghis khan (Pangasius sanitwongsei ) merupakan salah satu spesies ikan...

Asuka Langley SoryuTokoh Neon Genesis EvangelionPenampilanperdanaEpisode 8PenciptaGainaxHideaki AnnoYoshiyuki SadamotoPengisi suaraBahasa Jepang:Yūko MiyamuraBahasa Inggris:Tiffany GrantBiodataAliasAsuka Shikinami Langley (Rebuild)[1]GelarChildren KeduaKapten (Rebuild)KerabatKyoko Zeppelin Soryu (ibu)Ryoji Kaji (wali)Misato Katsuragi (wali)KewarganegaraanAmerikaAsuka Langley Soryu (惣流・アスカ・ラングレーcode: ja is deprecated , Sōryū Asuka Rangurē) adalah tokoh fikti...

Sharad Govindrao Pawar Sharad Govindrao Pawar (lahir 12 Desember 1940)[1] adalah seorang politikus asal India yang menjabat sebagai presiden Partai Kongres Nasionalis yang ia dirikan pada 1999, setelah terpisah dari Kongres Nasional India. Ia sebelumnya menjabat sebagai Ketua Menteri Maharashtra pada tiga masa jabatan terpisah dan memegang jabatan Menteri Pertahanan dan Menteri Pertanian dalam Pemerintahan India. Pawar berasal dari kota Baramati di distrik Pune, Maharashtra. Referensi...

Alan Greenspan, Ketua Dewan Gubernur Federal Reserve Amerika Serikat (1987—2006) Dalam kebijakan moneter Amerika Serikat, istilah Fedspeak (juga dikenal dengan nama Greenspeak) adalah sesuatu yang disebut Alan Blinder sebagai dialek bahasa Inggris kelewatan yang dipakai oleh ketua Dewan Federal Reserve dengan mengeluarkan pernyataan bertele-tele, meragukan, dan ambigu.[1][2][3] Strategi yang sering dipakai oleh Alan Greenspan ini bertujuan mencegah pasar keuangan ber...

Public school in the United StatesSouth Shore Vocational Technical High SchoolLocation476 Webster St.,Hanover, Massachusetts 02339United StatesCoordinates42°08′52″N 70°51′48″W / 42.14778°N 70.86333°W / 42.14778; -70.86333InformationTypePublicSuperintendentThomas HickeyPrincipalSandra BaldnerGrades9–12Enrollment600CampusSuburbanColor(s)Green, Gold & White MascotVikingNewspaperValhalla Times(discontinued)Budget$13,581,366 total$21,94...

Tandon di Colors Golden Petal Awards, 2012 Raveena Tandon adalah seorang pemeran asal India yang dikenal atas karyanya dalam perfilman Bollywood. Ia membuat debutnya dengan beradu peran bersama Salman Khan dalam film tahun 1991 Patthar Ke Phool, yang membuatnya meraih Penghargaan Filmfare untuk Wajah Baru Tahun Ini.[1] Ini disusul oleh serangkaian film gagal yang meliputi Ek Hi Raasta (1993) dan Parampara (1993).[1][2] Pada 1994, ia tampil dalam delapan film Hindi, keb...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (ديسمبر 2018) وايشان 武夷山市 خريطة الموقع تقسيم إداري البلد الصين[1] التقسيم الأعل...

When a country's central bank lacks the foreign reserves to maintain a fixed exchange rate A currency crisis is a type of financial crisis, and is often associated with a real economic crisis. A currency crisis raises the probability of a banking crisis or a default crisis. During a currency crisis the value of foreign denominated debt will rise drastically relative to the declining value of the home currency. Generally doubt exists as to whether a country's central bank has sufficient foreig...

Questa voce sull'argomento contee della Carolina del Nord è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Contea di JacksonconteaLocalizzazioneStato Stati Uniti Stato federato Carolina del Nord AmministrazioneCapoluogoSylva Data di istituzione1852 TerritorioCoordinatedel capoluogo35°17′24″N 83°08′24″W / 35.29°N 83.14°W35.29; -83.14 (Contea di Jackson)Coordinate: 35°17′24″N 83°08′24″W / ...

Questa voce sull'argomento sport invernali è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. A questa voce o sezione va aggiunto il template sinottico {{Sport}} Puoi aggiungere e riempire il template secondo le istruzioni e poi rimuovere questo avviso. Se non sei in grado di riempirlo in buona parte, non fare nulla; non inserire template vuoti. Lo stock sport o ice stock, altrimenti d...

You can help expand this article with text translated from the corresponding article in French. (March 2015) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedi...

الدوري الوطني 2002–03 تفاصيل الموسم دوري الدرجة الخامسة الإنجليزي [لغات أخرى] النسخة 24 البلد المملكة المتحدة البطل يوفل تاون الدوري الوطني 2001–02 الدوري الوطني 2003–04 تعديل مصدري - تعديل الدوري الوطني 2002–03 هو موسم من الدوري الوطني [لغات أ...

Melinda BamLahirMelinda de Kok14 Mei 1989 (umur 35)[1]Pretoria, Afrika SelatanAlmamaterUniversitas PretoriaPekerjaanModel, penulis, pelukis, perancang busana[2][3]Tinggi1,70 m (5 ft 7 in)GelarMiss South Africa 2011Pemenang kontes kecantikanWarna rambutPirangWarna mataCokelatKompetisiutamaMiss South Africa 2011(Pemenang)(Miss Tropika)(Me Waterkloof and Candy Girl pageants)Miss Universe 2012 (Top 10) Melinda Bam (lahir 14 Mei 1989) adalah seorang mod...

Spouse of a reigning British monarch For the royal consorts of the predecessor realms of England, Scotland, and Ireland, see List of English royal consorts, List of Scottish royal consorts, and List of Irish royal consorts. Prince Philip, Duke of Edinburgh, the husband of Queen Elizabeth II, was the longest-serving royal consort.Queen Camilla is the current consort as the wife of King Charles III. A royal consort is the spouse of a reigning monarch. Consorts of British monarchs have no const...

Caldera in British Columbia, Canada Silverthrone CalderaThe approximate outline of the Silverthrone CalderaHighest pointElevation3,160 m (10,370 ft)[1]ListingList of volcanoes in CanadaList of Cascade volcanoesCoordinates51°26′00″N 126°18′00″W / 51.43333°N 126.30000°W / 51.43333; -126.30000GeographyLocationBritish Columbia, CanadaParent rangePacific RangesGeologyAge of rockHoloceneMountain typeCaldera complexVolcanic arc/beltCanadian ...

Voce principale: David di Donatello (premio). Luca Bigazzi con sette premi detiene il record di vittorie. Il David di Donatello per il miglior autore della fotografia è un premio cinematografico assegnato annualmente nell'ambito dei David di Donatello, a partire dalla edizione del 1981[1]. Nato come David di Donatello per il miglior direttore della fotografia, dall'edizione del 2015 si chiama David di Donatello per il miglior autore della fotografia.[2] Il premio è stato vi...

Кубок Колумбии по футболу Основан 1950 Регион Колумбия Число участников 36 Действующий победитель Атлетико Насьональ (5) Наиболее титулован Атлетико Насьональ (5) Сайт Dimayor.com Кубок Колумбии 2024 Кубок Колумбии по футболу — клубный турнир по футболу в Колумбии, второй по зна...

У этого термина существуют и другие значения, см. Stratovarius (значения). Stratovarius Stratovarius на Wacken Open Air 2022, слева направо: Купиайнен, Котипелто, Пилве, Порра Основная информация Жанр пауэр-металнеоклассический метал[1]прогрессивный метал[1] Годы 1984 — настоящее время Страна &...

Questa voce sull'argomento artisti marziali statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Belal MuhammadNazionalità Stati Uniti Altezza178 cm Peso77 kg Arti marziali miste SpecialitàLotta libera CategoriaPesi welter Squadra Roufusport CarrieraSoprannomeRemember the Name Combatte da Illinois, Stati Uniti Incontri disputati28 Vittorie24 per knockout5 per sottomissione1 per decisione18 Sconfitte3 per knockout1 pe...