Перманент
|
Read other articles:

Cerambyx cerdo Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Genus: Cerambyx Spesies: Cerambyx cerdo Cerambyx cerdo adalah spesies kumbang tanduk panjang yang tergolong famili Cerambycidae. Spesies ini juga merupakan bagian dari genus Cerambyx, ordo Coleoptera, kelas Insecta, filum Arthropoda, dan kingdom Animalia. Larva kumbang ini biasanya mengebor ke dalam kayu dan dapat menyebabkan kerusakan pada batang kayu hidup atau kayu y...

Irene Kharisma SukandarIrine Kharisma Sukandar di Asian Indoor Games pada Juli 2013Asal negaraIndonesiaGelarMaster Internasional (2014)Woman Grandmaster (2009)Rating FIDE2413 (Agustus 2021)Rating tertinggi2432 (September 2016) Irene Kharisma Sukandar (lahir 7 April 1992) adalah seorang pecatur Indonesia pertama yang berhasil menyandang gelar Master Internasional (MI) terhitung mulai tahun 2014. Karier Sukandar sebagai peraih medali perak berdiri di antara Turmunkh Munkhzul dan ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2017. Eugene KilloranInformasi pribadiNama lengkap Eugene KilloranTanggal lahir 4 November 1987 (umur 36)Tempat lahir Tokyo, JepangPosisi bermain BekKarier senior*Tahun Tim Tampil (Gol)2006-2007 Tokyo Verdy * Penampilan dan gol di klub senior hanya dihitu...

American social worker Molly Dewson and Polly Porter, Van Cortlandt Park, Bronx 1925 Mary G. Polly Porter (March 1884 - 1972) was a social worker and for more than 50 years the partner of Mary Dewson, feminist and political activist. Porter was a close friend of Eleanor Roosevelt and part of her tight-knit circle of female friends. Biography Mary G. Porter, born in March, 1884, was the daughter of William D. Porter and Mabel G. Porter. Porter was independently wealthy and bred and raised Shel...

Bagian dari seriPendidikan di Indonesia Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi Republik Indonesia Pendidikan anak usia dini TK RA KB Pendidikan dasar (kelas 1–6) SD MI Paket A Pendidikan dasar (kelas 7–9) SMP MTs Paket B Pendidikan menengah (kelas 10–12) SMA MA SMK MAK SMA SMTK SMAK Utama Widya Pasraman Paket C Pendidikan tinggi Perguruan tinggi Akademi Akademi komunitas Institut Politeknik Sekolah tinggi Universitas Lain-lain Madrasah Pesantren Sekolah alam Sekolah ru...

ThinkQuestBeranda dari Halaman ThinkQuestURLwww.thinkquest.orgTipeSitus web EdukasiPerdagangan ?YaRegistration (en)DibutuhkanLangueMultibahasa (60)PemilikOracle Education FoundationPembuatAllan H. WeisService entry (en)1996 (Acquired by Oracle in 2002)Peringkat Alexa717.006 (30 November 2017) KeadaanAktif Oracle Thinkquest adalah sebuah situs web pembelajaran daring yang disponsori oleh Oracle Education Foundation. Situs web ini dikhususkan untuk pelajar dari Sekolah Dasar hingga Sekolah...

Kereta Rel Diesel IndonesiaKereta api komuter SuPor yang menggunakan KRDI ACBeroperasiYaPembuatPT InkaTahun pembuatan2007-2014Mulai beroperasi2008-sekarangJumlah sudah diproduksi13 setFormasi 4 kereta per set 2 kereta per set (khusus KA Cut Meutia) OperatorPT Kereta Api IndonesiaData teknisBodi keretaMild steel, MonocoquePanjang rangkaian80.000 mmPanjang kereta20.000 mmLebar2.990 mmTinggi3.830 mmKecepatan maksimum120 km/jamBerat MeC; 41 ton T: 32 ton MesinCummins N14 RJenis mesinHorizontal in...
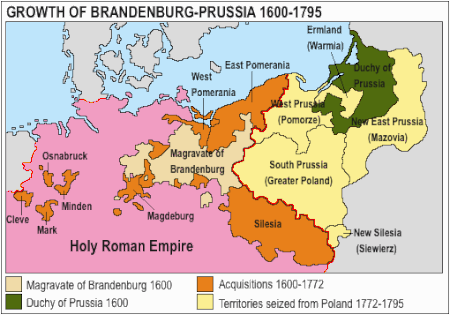
La provincia della Prussia meridionale nel Regno di Prussia. La Prussia meridionale (in tedesco: Südpreußen) fu una provincia del Regno di Prussia dal 1793 al 1806. Fu creata dopo la seconda spartizione della Polonia e includeva anche la regione della Grande Polonia. La principale città era Poznań. Nel 1806 aveva 1.503.508 abitanti. La Prussia meridionale fu amministrata dal Direttorio Generale a Berlino fino al 1806. I coloni tedeschi invitati a insediarsi nelle tenute nobiliari della pr...

Acido stearolico Nome IUPACAcido octadecen-9-inoico Abbreviazioni18:1Δ9a Caratteristiche generaliFormula bruta o molecolareC18H32O2 Massa molecolare (u)280,4 Numero CAS506-24-1 Numero EINECS208-030-8 PubChem68167 SMILESCCCCCCCCC#CCCCCCCCC(=O)O Indicazioni di sicurezzaFrasi H--- Consigli P--- Modifica dati su Wikidata · Manuale L'acido stearolico è un acido grasso acetilenico con 18 atomi di carbonio, un legame triplo in posizione 9≡10, descritto in notazione delta come 18:...

Albanian Basketball FederationFounded1946; 76 years agoAffiliationFIBAAffiliation date1947; 75 years agoRegional affiliationFIBA EuropeAffiliation date1947; 75 years agoHeadquartersTiranaPresidentAvni PonariOfficial websitefshb.basketball The Albanian Basketball Federation (Albanian: Federata Shqiptare e Basketbollit; FSHB) is the governing body of basketball in Albania. It is based in Tirana, Albania. It organises the national basketball leagues of the Albanian Superliga, the First Division,...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

2020 single by Rise AgainstBroken Dreams, IncSingle by Rise Againstfrom the album Nowhere Generation ReleasedSeptember 16, 2020GenreHardcore punk Melodic hardcore Length3:53LabelLoma VistaSongwriter(s) Tim McIlrath Joe Principe Brandon Barnes Zach Blair Producer(s) Bill Stevenson Jason Livermore Andrew Berlin Chris Beeble Rise Against singles chronology House on Fire (2018) Broken Dreams, Inc (2020) Nowhere Generation (2021) Broken Dreams, Inc is a song by American punk rock band Rise Against...

1957 film by Roger Corman Teenage DollTheatrical release posterDirected byRoger CormanWritten byCharles B. GriffithProduced byRoger CormanexecutiveBernard WoolnerassociateLawrence WoolnerStarringJune KenneyJohn BrinkleyFay SpainCinematographyFloyd CrosbyMusic byWalter GreeneProductioncompanyWoolner BrothersDistributed byAllied ArtistsRelease date September 18, 1957 (1957-09-18) Running time71 min.CountryUnited StatesLanguageEnglish Teenage Doll is a 1957 film noir directed by R...

Cet article est une ébauche concernant une chanteuse espagnole et le Concours Eurovision de la chanson. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Patricia KrausBiographieNaissance 4 janvier 1964 (60 ans)MilanNationalité espagnoleActivité ChanteusePériode d'activité depuis 1987Père Alfredo KrausAutres informationsGenre artistique PopSite web www.patriciakraus.esmodifier - modifier le code - modif...

这是马来族人名,“尤索夫”是父名,不是姓氏,提及此人时应以其自身的名“法迪拉”为主。 尊敬的拿督斯里哈芝法迪拉·尤索夫Fadillah bin Haji YusofSSAP DGSM PGBK 国会议员 副首相 第14任马来西亚副首相现任就任日期2022年12月3日与阿末扎希同时在任君主最高元首苏丹阿都拉陛下最高元首苏丹依布拉欣·依斯迈陛下首相安华·依布拉欣前任依斯迈沙比里 马来西亚能源转型与�...

Taraba's delegation in Nigeria's National Assembly Politics of Nigeria Constitution Human rights Government President (list) Bola Tinubu Vice President Kashim Shettima Cabinet Federal Parastatals Legislature National Assembly of Nigeria Senate President Godswill Akpabio (APC) Deputy President Barau Jibrin (APC) (List of members of the Senate) House of Representatives Speaker Abbas Tajudeen (APC) Deputy Speaker Benjamin Okezie Kalu (APC) (List of members of the House) State delegations Abia Ad...

Census-designated place in Texas, United StatesMcQueeney, TexasCensus-designated placeLocation of McQueeney, TexasCoordinates: 29°35′53″N 98°2′36″W / 29.59806°N 98.04333°W / 29.59806; -98.04333CountryUnited StatesStateTexasCountyGuadalupeArea • Total4.6 sq mi (11.8 km2) • Land4.2 sq mi (10.8 km2) • Water0.4 sq mi (1.0 km2)Elevation548 ft (167 m)Population (2020)...

Arid region of south-central Wyoming, United States The Killpecker Sand Dunes of the Red Desert support a wide range of wildlife and vegetation, ranging from elk who use the adjoining sagebrush steppe for shelter to aquatic organisms that thrive in snowmelt ponds. Photo by the Bureau of Land Management. The Red Desert is a high-altitude desert and sagebrush steppe located in the south-central portion of the U.S. state of Wyoming, comprising approximately 9,320 square miles (24,100 square kilo...

Weightlifting at the Olympics Weightliftingat the Games of the XVII OlympiadVenuePalazzetto dello SportDates7–10 September 1960Competitors172 from 53 nations← 19561964 → Weightlifting at the1960 Summer OlympicsMen56 kg60 kg67.5 kg75 kg82.5 kg90 kg+90 kgvte The weightlifting competition at the 1960 Summer Olympics in Rome consisted of seven weight classes, all for men only.[1] Medal summary Games Gold Silver Bronze 56 kgdetails Charles Vinci ...

Hipertensi intrakranial idiopatik (HII), adalah kondisi yang ditandai dengan peningkatan tekanan intrakranial tanpa adanya penyebab pasti yang bisa diketahui secara pasti. Dikenal juga dengan nama pseudomotor serebri atau hipertensi intrakranial benigna.[1][2][3] Kondisi ini pertama kali digambarkan oleh Quicke pada tahun 1897.[1][4] HII ini memberikan gejala yang menyerupai gejala tumor otak walaupun dengan pencitraan kepala, tumornya tidak akan ditem...









































