Парадокс Ришара
|
Read other articles:

Ibrani 1Surat Ibrani 1:7-12 pada naskah Papirus 114, yang dibuat sekitar tahun 250 M.KitabSurat IbraniKategoriSurat-surat Paulus/Surat-surat AmBagian Alkitab KristenPerjanjian BaruUrutan dalamKitab Kristen19← Surat Filemon pasal 2 → Ibrani 1 (disingkat Ibr 1) adalah pasal pertama Surat kepada Orang Ibrani dalam Perjanjian Baru di Alkitab Kristen.[1][2] Tidak diketahui pengarangnya, selain dari informasi bahwa ia seorang laki-laki (berdasarkan jenis kata yang dipaka...
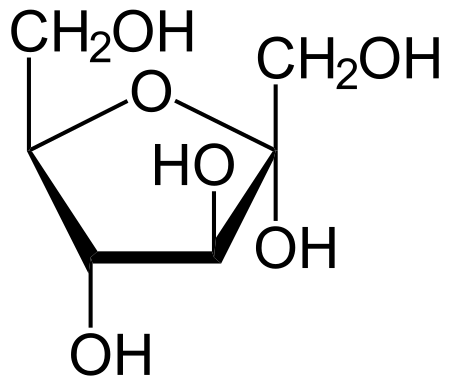
Fruktosa, salah satu jenis monosakarida. Monosakarida (dari Bahasa Yunani mono: satu, sacchar: gula) adalah senyawa karbohidrat dalam bentuk gula yang paling sederhana.[1][2].Gugus fungsi yang menyusun monosakarida adalah satu unit aldehid atau keton. Dalam bentuk stereoisomer, monosakarida memiliki sedikitnya satu atom karbon asimetrik.[3] Monosakarida terbentuk dari hasil sintesis senyawa sederhana melalui proses glukoneogenesis. Pembentukan monosakarida juga dapat d...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (مارس 2018) مقاطعة إيغل الإحداثيات 39°37′N 106°42′W / 39.62°N 106.7°W / 39.62; -106.7 ...

Awe5ome Baby Awe5ome Baby adalah sebuah grup vokal Korea Selatan di bawah kontrak TN Nation Entertainment.[1][2] Grup tersebut terdiri dari Kim Jun Hee, Son Soo Min, Kim Ye Chan, Lee Da Hee, dan Jung Yoon Hye. Grup tersebut debut pada 19 Juni 2015 dengan merilis album singel Why me?. Grup tersebut resmi bubar pada 4 Desember 2016. Salah satu anggotanya, Kim Yechan, kemudian masuk ke grup Pink Fantasy. Referensi ^ 은지영 (2015-06-19). '뮤직뱅크' 어썸베이비, '내가 ...

1973 1981 Élections législatives françaises de 1978 491 députés de l'Assemblée nationale(majorité absolue : 246 sièges) 12 et 19 mars 1978 Corps électoral et résultats Votants au 1er tour 28 560 243 82,78 % 1,5 Votants au 2d tour 25 475 802 84,66 % Majorité présidentielle – Raymond Barre Liste Rassemblement pour la RépubliqueUnion pour la démocratie françaiseDivers droite Voix au 1er tour 13 276 2...

H.Tri KurniadiS.H., M.Si.Berkas:Walkot Jaksel Tri Kurniadi.jpg Wali Kota Administrasi Jakarta Selatan ke-14Masa jabatan13 Agustus 2015 – 5 Juli 2018PresidenJoko WidodoGubernurBasuki Tjahaja Purnama Djarot Saiful Hidayat Anies BaswedanWakilArifin PendahuluSyamsuddin NoorPenggantiMarullah MataliWakil Wali Kota Jakarta SelatanMasa jabatan2 Januari 2015 – 13 Agustus 2015PresidenJoko WidodoGubernurBasuki Tjahaja PurnamaWali KotaSyamsuddin Noor PendahuluTri Djoko Sri Margi...

Member of the Cabinet of the United Kingdom This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Secretary of State for Work and Pensions – news · newspapers · books · scholar · JSTOR (May 2019) (Learn how and when to remove this template message) United Kingdom Secretary of Statefor Work and PensionsRoyal Arms o...

CEST beralih ke halaman ini. Untuk kegunaan lain, lihat CEST (disambiguasi). Zona Waktu di Eropa: biru muda Waktu Eropa Barat (UTC+0) biru Waktu Eropa Barat (UTC+0) Waktu Musim Panas Eropa Barat (UTC+01:00) merah muda Waktu Eropa Tengah (UTC+01:00) merah Waktu Eropa Tengah (UTC+01:00) Waktu Musim Panas Eropa Tengah (UTC+02:00) kuning Waktu Kaliningrad (UTC+02:00) emas Waktu Eropa Timur (UTC+02:00) Waktu Musim Panas Eropa Timur (UTC+03:00) hijau muda Waktu Minsk, Waktu Moskwa (UTC+03:00) Warna...

American prelate William ScullyBishop of AlbanyProvinceNew YorkDioceseAlbanyInstalled1945Term ended1969PredecessorEdmund Gibbons †SuccessorEdwin Broderick †Other post(s)Titular Bishop of PharsalusOrdersOrdinationSeptember 20, 1919ConsecrationOctober 24, 1945Personal detailsBorn(1894-08-06)August 6, 1894New York CityDiedJanuary 5, 1969(1969-01-05) (aged 74)Albany, New YorkNationality AmericanDenominationRoman Catholic ChurchAlma materCatholic University of America William Aloysiu...

Mercy Otis WarrenMercy Otis Warren par John Singleton Copley.BiographieNaissance 14 septembre 1728BarnstableDécès 19 octobre 1814 (à 86 ans)PlymouthSépulture Old Burial Hill (en)Pseudonyme A Columbian PatriotNationalité américaineActivités Dramaturge, poétesse, écrivaine, historienne, philosophePère James Otis, Sr. (en)Mère Mary Allyn (d)Fratrie James OtisSamuel Allyne Otis (en)Conjoint James WarrenEnfant Henry Warren (d)Autres informationsDistinction National Women's Hall of ...

Voce principale: Appio Latino Metronio Associazione Sportiva. Gruppo Sportivo Almas RomaStagione 1978-1979Sport calcio Squadra ALMAS Allenatore Amos Cardarelli Presidente Silvestro De Angelis Serie C29º nel girone A Maggiori presenzeCampionato: Anzuini, Savio (34) Miglior marcatoreCampionato: Forte (13) 1977-1978 1979-1980 Si invita a seguire il modello di voce Questa pagina raccoglie le informazioni riguardanti l'ALMAS Roma nelle competizioni ufficiali della stagione 1978-1979. Indice...

President of India from 2017 to 2022 Kovind redirects here. For his wife, see Savita Kovind. Ram Nath KovindOfficial portrait, 201714th President of IndiaIn office25 July 2017 – 25 July 2022Prime MinisterNarendra ModiVice PresidentMohammad Hamid AnsariM. Venkaiah NaiduPreceded byPranab MukherjeeSucceeded byDroupadi Murmu26th Governor of BiharIn office16 August 2015 – 21 June 2017Chief MinisterNitish KumarPreceded byKeshari Nath TripathiSucceeded byKeshari Nath Tr...

Perincian utang pemerintah Puerto Riko Krisis utang pemerintahan Puerto Riko adalah sebuah krisis keuangan yang berhubungan dengan jumlah utang pemerintah Puerto Riko. Pemerintah tersebut memiliki utang lebih dari US$70 miliar dengan rasio 68%.[a] Pada Februari 2014, beberapa lembaga pemeringkat kredit menurunkan utang pemerintah menjadi taraf non-inventasi. Krisis ini menyebabkan pemerintah Puerto Riko mengadopsi kebijakan yang idealnya menurunkan biaya secara drastis, meningkatkan p...

「俄亥俄」重定向至此。关于其他用法,请见「俄亥俄 (消歧义)」。 俄亥俄州 美國联邦州State of Ohio 州旗州徽綽號:七葉果之州地图中高亮部分为俄亥俄州坐标:38°27'N-41°58'N, 80°32'W-84°49'W国家 美國加入聯邦1803年3月1日,在1953年8月7日追溯頒定(第17个加入联邦)首府哥倫布(及最大城市)政府 • 州长(英语:List of Governors of {{{Name}}}]]) •&...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (يوليو 2018) يحكى أن برنامج أسبوعي من تقديم الإعلامي أسعد طه وتبثه قناة الجزيرة الفضائية.[...

American diplomat (1870–1959) Ulysses S. Grant-SmithUnited States Minister to Uruguay In officeJuly 13, 1925 – January 11, 1929PresidentCalvin CoolidgePreceded byHerman Hoffman PhilipSucceeded byLeland B. Harrison1st United States Minister to Albania In officeDecember 4, 1922 – February 8, 1925PresidentWarren G. Harding Calvin CoolidgePreceded byDiplomatic relations establishedSucceeded byCharles C. Hart Personal detailsBorn(1870-11-18)November 18, 1870Washington, Penn...

Australian TV series or program In Pit LaneGenreMotorsport programPresented byBrett RamseyCountry of originAustraliaOriginal languageEnglishProductionProduction locationsRMIT University Melbourne, VictoriaRunning time30 minutes (including sponsorships)Production companiesRMITV (Student Community Television Inc.)RMIT Student UnionOriginal releaseNetworkC31 (1998 - )Optus Vision (1996-1998 )Release1996 (1996) In Pit Lane presenter Brett Ramsey in September 2006 In Pit Lane is an Australia...