–Ě–ĺ—Ä–ľ–įŐĀ–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–ĶŐĀ–Ĺ–ł–Ķ [ 1] [ 2] —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ–ľ –ď–į—É—Ā—Ā–į –ł–Ľ–ł –ď–į—É—Ā—Ā–į ‚ÄĒ –õ–į–Ņ–Ľ–į—Ā–į [ 3] –ļ–ĺ–Ľ–ĺ–ļ–ĺ–Ľ–ĺ–ĺ–Ī—Ä–į–∑–Ĺ–į—Ź –ļ—Ä–ł–≤–į—Ź ‚ÄĒ –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–Ķ–Ļ —Ā –Ņ–ł–ļ–ĺ–ľ –≤ —Ü–Ķ–Ĺ—ā—Ä–Ķ –ł —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ—č–ľ–ł –Ī–ĺ–ļ–ĺ–≤—č–ľ–ł —Ā—ā–ĺ—Ä–ĺ–Ĺ–į–ľ–ł, –ļ–ĺ—ā–ĺ—Ä–ĺ–Ķ –≤ –ĺ–ī–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ–ľ —Ā–Ľ—É—á–į–Ķ –∑–į–ī–į—Ď—ā—Ā—Ź —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā–ł –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł , —Ā–ĺ–≤–Ņ–į–ī–į—é—Č–Ķ–Ļ —Ā —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ –ď–į—É—Ā—Ā–į :
f
(
x
)
=
1
σ ŌÉ -->
2
π ŌÄ -->
e
− ‚ąí -->
1
2
(
x
− ‚ąí -->
μ őľ -->
σ ŌÉ -->
)
2
{\displaystyle f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}}
–≥–ī–Ķ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä
μ őľ -->
{\displaystyle \mu }
–ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –ĺ–∂–ł–ī–į–Ĺ–ł–Ķ (—Ā—Ä–Ķ–ī–Ĺ–Ķ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ), –ľ–Ķ–ī–ł–į–Ĺ–į –ł –ľ–ĺ–ī–į —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź, –į –Ņ–į—Ä–į–ľ–Ķ—ā—Ä
σ ŌÉ -->
{\displaystyle \sigma }
—Ā—Ä–Ķ–ī–Ĺ–Ķ–ļ–≤–į–ī—Ä–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –ĺ—ā–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł–Ķ ,
σ ŌÉ -->
2
{\displaystyle \sigma ^{2}}
–ī–ł—Ā–Ņ–Ķ—Ä—Ā–ł—Ź —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –ĺ–ī–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ–Ķ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ī–≤—É—Ö–Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–ľ —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–ĺ–ľ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ļ, –ļ–ĺ—ā–ĺ—Ä–ĺ–Ķ –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–ł—ā —ć–ļ—Ā–Ņ–ĺ–Ĺ–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ–ĺ–ľ—É –ļ–Ľ–į—Ā—Ā—É —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ļ[ 4] –ú–Ĺ–ĺ–≥–ĺ–ľ–Ķ—Ä–Ĺ–ĺ–Ķ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ ¬Ľ.
–°—ā–į–Ĺ–ī–į—Ä—ā–Ĺ—č–ľ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ—č–ľ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ–ľ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —Ā –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–ľ –ĺ–∂–ł–ī–į–Ĺ–ł–Ķ–ľ
μ őľ -->
=
0
{\displaystyle \mu =0}
σ ŌÉ -->
=
1.
{\displaystyle \sigma =1.}
–ē—Ā–Ľ–ł –≤–Ķ–Ľ–ł—á–ł–Ĺ–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ā—É–ľ–ľ–ĺ–Ļ –ľ–Ĺ–ĺ–≥–ł—Ö —Ā–Ľ—É—á–į–Ļ–Ĺ—č—Ö —Ā–Ľ–į–Ī–ĺ –≤–∑–į–ł–ľ–ĺ–∑–į–≤–ł—Ā–ł–ľ—č—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ, –ļ–į–∂–ī–į—Ź –ł–∑ –ļ–ĺ—ā–ĺ—Ä—č—Ö –≤–Ĺ–ĺ—Ā–ł—ā –ľ–į–Ľ—č–Ļ –≤–ļ–Ľ–į–ī –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ĺ–Ī—Č–Ķ–Ļ —Ā—É–ľ–ľ—č, —ā–ĺ —Ü–Ķ–Ĺ—ā—Ä–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ķ –ł –Ĺ–ĺ—Ä–ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —ā–į–ļ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č –Ņ—Ä–ł –ī–ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ –Ī–ĺ–Ľ—Ć—ą–ĺ–ľ —á–ł—Ā–Ľ–Ķ —Ā–Ľ–į–≥–į–Ķ–ľ—č—Ö —Ā—ā—Ä–Ķ–ľ–ł—ā—Ā—Ź –ļ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–ľ—É —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é .
–≠—ā–ĺ —Ā–Ľ–Ķ–ī—É–Ķ—ā –ł–∑ —Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ—Ä–Ķ–ī–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —ā–Ķ–ĺ—Ä–Ķ–ľ—č —ā–Ķ–ĺ—Ä–ł–ł –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–Ķ–Ļ . –í –ĺ–ļ—Ä—É–∂–į—é—Č–Ķ–ľ –Ĺ–į—Ā –ľ–ł—Ä–Ķ —á–į—Ā—ā–ĺ –≤—Ā—ā—Ä–Ķ—á–į—é—ā—Ā—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ—č, –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –ļ–ĺ—ā–ĺ—Ä—č—Ö –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź —Ā–ĺ–≤–ĺ–ļ—É–Ņ–Ĺ–ĺ—Ā—ā—Ć—é –ľ–Ĺ–ĺ–≥–ł—Ö –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ—č—Ö —Ą–į–ļ—ā–ĺ—Ä–ĺ–≤. –≠—ā–ĺ—ā —Ą–į–ļ—ā, –į —ā–į–ļ–∂–Ķ —ā–ĺ, —á—ā–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —Ā—á–ł—ā–į–Ľ–ĺ—Ā—Ć —ā–ł–Ņ–ł—á–Ĺ—č–ľ, –ĺ–Ī—č—á–Ĺ—č–ľ, –Ņ—Ä–ł–≤–Ķ–Ľ–ł –ļ —ā–ĺ–ľ—É, —á—ā–ĺ –≤ –ļ–ĺ–Ĺ—Ü–Ķ XIX –≤–Ķ–ļ–į —Ā—ā–į–Ľ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć—Ā—Ź —ā–Ķ—Ä–ľ–ł–Ĺ ¬ę–Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ¬Ľ. –Ě–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –ł–≥—Ä–į–Ķ—ā –∑–į–ľ–Ķ—ā–Ĺ—É—é —Ä–ĺ–Ľ—Ć –≤–ĺ –ľ–Ĺ–ĺ–≥–ł—Ö –ĺ–Ī–Ľ–į—Ā—ā—Ź—Ö –Ĺ–į—É–ļ–ł, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä –≤ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā—ā–į—ā–ł—Ā—ā–ł–ļ–Ķ –ł —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą–ł–∑–ł–ļ–Ķ .
–°–Ľ—É—á–į–Ļ–Ĺ–į—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–į, –ł–ľ–Ķ—é—Č–į—Ź –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ, –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ļ, –ł–Ľ–ł –≥–į—É—Ā—Ā–ĺ–≤—Ā–ļ–ĺ–Ļ, —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ–Ļ.
–Ě–į–ł–Ī–ĺ–Ľ–Ķ–Ķ –Ņ—Ä–ĺ—Ā—ā–ĺ–Ļ —Ā–Ľ—É—á–į–Ļ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź ‚ÄĒ —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ–ĺ–Ķ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ ‚ÄĒ —á–į—Ā—ā–Ĺ—č–Ļ —Ā–Ľ—É—á–į–Ļ, –ļ–ĺ–≥–ī–į
μ őľ -->
=
0
{\displaystyle \mu =0}
σ ŌÉ -->
=
1.
{\displaystyle \sigma =1.}
–Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā—Ć –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł —Ä–į–≤–Ĺ–į:
φ ŌÜ -->
(
x
)
=
1
2
π ŌÄ -->
e
− ‚ąí -->
1
2
x
2
.
{\displaystyle \varphi (x)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}x^{2}}.}
–ú–Ĺ–ĺ–∂–ł—ā–Ķ–Ľ—Ć
1
2
π ŌÄ -->
{\displaystyle {\frac {1}{\sqrt {2\pi }}}}
∫ ‚ąę -->
− ‚ąí -->
∞ ‚ąě -->
+
∞ ‚ąě -->
φ ŌÜ -->
(
x
)
d
x
=
1
{\displaystyle \int \limits _{-\infty }^{+\infty }\varphi (x)\,dx=1}
[ 5]
1
2
{\displaystyle {\frac {1}{2}}}
x
=
0
,
{\displaystyle x=0,}
1
2
π ŌÄ -->
.
{\displaystyle {\frac {1}{\sqrt {2\pi }}}.}
–Ę–ĺ—á–ļ–ł –Ņ–Ķ—Ä–Ķ–≥–ł–Ī–į —Ą—É–Ĺ–ļ—Ü–ł–ł:
x
=
+
1
{\displaystyle x=+1}
x
=
− ‚ąí -->
1.
{\displaystyle x=-1.}
–ď–į—É—Ā—Ā –Ĺ–į–∑—č–≤–į–Ľ —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ—č–ľ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ—č–ľ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —Ā
σ ŌÉ -->
2
=
1
/
2
,
{\displaystyle \sigma ^{2}=1/2,}
φ ŌÜ -->
(
x
)
=
e
− ‚ąí -->
x
2
π ŌÄ -->
.
{\displaystyle \varphi (x)={\frac {e^{-x^{2}}}{\sqrt {\pi }}}.}
–ö–į–∂–ī–ĺ–Ķ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ ‚ÄĒ —ć—ā–ĺ –≤–į—Ä–ł–į–Ĺ—ā —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ–ĺ–≥–ĺ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź, –ĺ–Ī–Ľ–į—Ā—ā—Ć –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ļ –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ —Ä–į—Ā—ā—Ź–≥–ł–≤–į–Ķ—ā—Ā—Ź –ľ–Ĺ–ĺ–∂–ł—ā–Ķ–Ľ–Ķ–ľ
σ ŌÉ -->
{\displaystyle \sigma }
μ őľ -->
{\displaystyle \mu }
f
(
x
∣ ‚ą£ -->
μ őľ -->
,
σ ŌÉ -->
2
)
=
1
σ ŌÉ -->
φ ŌÜ -->
(
x
− ‚ąí -->
μ őľ -->
σ ŌÉ -->
)
.
{\displaystyle f(x\mid \mu ,\sigma ^{2})={\frac {1}{\sigma }}\varphi \left({\frac {x-\mu }{\sigma }}\right).}
μ őľ -->
,
σ ŌÉ -->
{\displaystyle \mu ,\sigma }
1
σ ŌÉ -->
,
{\displaystyle {\frac {1}{\sigma }},}
–ē—Ā–Ľ–ł
Z
{\displaystyle Z}
X
=
σ ŌÉ -->
Z
+
μ őľ -->
{\displaystyle X=\sigma Z+\mu }
μ őľ -->
{\displaystyle \mu }
σ ŌÉ -->
.
{\displaystyle \sigma .}
X
{\displaystyle X}
μ őľ -->
{\displaystyle \mu }
σ ŌÉ -->
2
,
{\displaystyle \sigma ^{2},}
Z
=
X
− ‚ąí -->
μ őľ -->
σ ŌÉ -->
{\displaystyle Z={\frac {X-\mu }{\sigma }}}
–ē—Ā–Ľ–ł –≤ —ć–ļ—Ā–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā–Ķ –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā–ł –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł —Ä–į—Ā–ļ—Ä—č—ā—Ć —Ā–ļ–ĺ–Ī–ļ–ł –ł —É—á–ł—ā—č–≤–į—ā—Ć, —á—ā–ĺ
1
=
ln
‚Ā° -->
e
{\displaystyle 1=\ln e}
f
(
x
)
=
1
σ ŌÉ -->
2
π ŌÄ -->
e
− ‚ąí -->
1
2
(
x
− ‚ąí -->
μ őľ -->
σ ŌÉ -->
)
2
=
e
− ‚ąí -->
1
2
(
2
ln
‚Ā° -->
σ ŌÉ -->
+
ln
‚Ā° -->
2
π ŌÄ -->
+
(
x
− ‚ąí -->
μ őľ -->
σ ŌÉ -->
)
2
)
=
e
− ‚ąí -->
1
2
(
x
2
σ ŌÉ -->
2
− ‚ąí -->
2
μ őľ -->
x
σ ŌÉ -->
2
+
2
ln
‚Ā° -->
σ ŌÉ -->
+
ln
‚Ā° -->
2
π ŌÄ -->
+
μ őľ -->
2
σ ŌÉ -->
2
)
.
{\displaystyle f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}=e^{-{\frac {1}{2}}\left(2\ln \sigma +\ln 2\pi +\left({\frac {x-\mu }{\sigma }}\right)^{2}\right)}=e^{-{\frac {1}{2}}\left({\frac {x^{2}}{\sigma ^{2}}}-2{\frac {\mu x}{\sigma ^{2}}}+2\ln \sigma +\ln 2\pi +{\frac {\mu ^{2}}{\sigma ^{2}}}\right)}.}
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā—Ć –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł –ļ–į–∂–ī–ĺ–≥–ĺ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ —ć–ļ—Ā–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—É –ļ–≤–į–ī—Ä–į—ā–ł—á–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł :
f
(
x
)
=
e
a
x
2
+
b
x
+
c
,
{\displaystyle f(x)=e^{ax^{2}+bx+c},}
–≥–ī–Ķ
a
=
− ‚ąí -->
1
2
σ ŌÉ -->
2
,
b
=
μ őľ -->
σ ŌÉ -->
2
,
c
=
− ‚ąí -->
(
ln
‚Ā° -->
σ ŌÉ -->
+
1
2
ln
‚Ā° -->
2
π ŌÄ -->
+
1
2
μ őľ -->
2
σ ŌÉ -->
2
)
.
{\displaystyle a=-{\frac {1}{2\sigma ^{2}}},\ b={\frac {\mu }{\sigma ^{2}}},\ c=-\left(\ln \sigma +{\frac {1}{2}}\ln 2\pi +{\frac {1}{2}}{\frac {\mu ^{2}}{\sigma ^{2}}}\right).}
–ě—ā—Ā—é–ī–į –ľ–ĺ–∂–Ĺ–ĺ –≤—č—Ä–į–∑–ł—ā—Ć —Ā—Ä–Ķ–ī–Ĺ–Ķ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –ļ–į–ļ
μ őľ -->
=
− ‚ąí -->
b
2
a
,
{\displaystyle \mu =-{\frac {b}{2a}},}
σ ŌÉ -->
2
=
− ‚ąí -->
1
2
a
.
{\displaystyle \sigma ^{2}=-{\frac {1}{2a}}.}
a
=
− ‚ąí -->
1
/
2
,
{\displaystyle a=-1/2,}
b
=
0
{\displaystyle b=0}
c
=
− ‚ąí -->
1
2
ln
‚Ā° -->
2
π ŌÄ -->
.
{\displaystyle c=-{\frac {1}{2}}\ln 2\pi .}
–ü–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā—Ć –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ–ĺ–≥–ĺ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź (—Ā –Ĺ—É–Ľ–Ķ–≤—č–ľ —Ā—Ä–Ķ–ī–Ĺ–ł–ľ –ł –Ķ–ī–ł–Ĺ–ł—á–Ĺ–ĺ–Ļ –ī–ł—Ā–Ņ–Ķ—Ä—Ā–ł–Ķ–Ļ) —á–į—Ā—ā–ĺ –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā—Ā—Ź –≥—Ä–Ķ—á–Ķ—Ā–ļ–ĺ–Ļ –Ī—É–ļ–≤–ĺ–Ļ
ϕ Ōē -->
{\displaystyle \phi }
—Ą–ł )[ 6]
φ ŌÜ -->
{\displaystyle \varphi }
–Ě–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —á–į—Ā—ā–ĺ –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā—Ā—Ź
N
(
μ őľ -->
,
σ ŌÉ -->
2
)
,
{\displaystyle N(\mu ,\sigma ^{2}),}
N
(
μ őľ -->
,
σ ŌÉ -->
2
)
{\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}
[ 7]
X
{\displaystyle X}
μ őľ -->
{\displaystyle \mu }
σ ŌÉ -->
2
,
{\displaystyle \sigma ^{2},}
X
∼ ‚ąľ -->
N
(
μ őľ -->
,
σ ŌÉ -->
2
)
.
{\displaystyle X\sim {\mathcal {N}}(\mu ,\sigma ^{2}).}
–§—É–Ĺ–ļ—Ü–ł—Ź —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ–ĺ–≥–ĺ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź (–Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ) –ĺ–Ī—č—á–Ĺ–ĺ –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā—Ā—Ź –∑–į–≥–Ľ–į–≤–Ĺ–ĺ–Ļ –≥—Ä–Ķ—á–Ķ—Ā–ļ–ĺ–Ļ –Ī—É–ļ–≤–ĺ–Ļ
Φ ő¶ -->
{\displaystyle \Phi }
—Ą–ł ), –≤ –†–ĺ—Ā—Ā–ł–ł –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ –õ–į–Ņ–Ľ–į—Ā–į –ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ:
Φ ő¶ -->
(
x
)
=
1
2
π ŌÄ -->
∫ ‚ąę -->
− ‚ąí -->
∞ ‚ąě -->
x
e
− ‚ąí -->
t
2
/
2
d
t
.
{\displaystyle \Phi (x)={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{x}e^{-t^{2}/2}\,dt.}
–° –Ĺ–Ķ–Ļ —Ā–≤—Ź–∑–į–Ĺ–į —Ą—É–Ĺ–ļ—Ü–ł—Ź –ĺ—ą–ł–Ī–ĺ–ļ (–ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł)
erf
‚Ā° -->
(
x
)
,
{\displaystyle \operatorname {erf} (x),}
[
− ‚ąí -->
x
,
x
]
{\displaystyle [-x,x]}
erf
‚Ā° -->
(
x
)
=
2
π ŌÄ -->
∫ ‚ąę -->
0
x
e
− ‚ąí -->
t
2
d
t
.
{\displaystyle \operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int \limits _{0}^{x}e^{-t^{2}}\,dt.}
–≠—ā–ł –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ—č –Ĺ–Ķ –≤—č—Ä–į–∂–į—é—ā—Ā—Ź –≤ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ—č—Ö —Ą—É–Ĺ–ļ—Ü–ł—Ź—Ö –ł –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ—č–ľ–ł —Ą—É–Ĺ–ļ—Ü–ł—Ź–ľ–ł . –ú–Ĺ–ĺ–≥–ł–Ķ –ł—Ö —á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ—č–Ķ –Ņ—Ä–ł–Ī–Ľ–ł–∂–Ķ–Ĺ–ł—Ź –ł–∑–≤–Ķ—Ā—ā–Ĺ—č. –°–ľ. –Ĺ–ł–∂–Ķ .
–§—É–Ĺ–ļ—Ü–ł–ł —Ā–≤—Ź–∑–į–Ĺ—č, –≤ —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł, —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ–ľ:
Φ ő¶ -->
(
x
)
=
1
2
[
1
+
erf
‚Ā° -->
(
x
2
)
]
{\displaystyle \Phi (x)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]}
–Ě–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —Ā –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā—Ć—é
f
,
{\displaystyle f,}
μ őľ -->
{\displaystyle \mu }
σ ŌÉ -->
{\displaystyle \sigma }
F
(
x
)
=
Φ ő¶ -->
(
x
− ‚ąí -->
μ őľ -->
σ ŌÉ -->
)
=
1
2
[
1
+
erf
‚Ā° -->
(
x
− ‚ąí -->
μ őľ -->
σ ŌÉ -->
2
)
]
.
{\displaystyle F(x)=\Phi \left({\frac {x-\mu }{\sigma }}\right)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right].}
–ú–ĺ–∂–Ĺ–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć —Ą—É–Ĺ–ļ—Ü–ł—é
Q
(
x
)
=
1
− ‚ąí -->
Φ ő¶ -->
(
x
)
{\displaystyle Q(x)=1-\Phi (x)}
X
{\displaystyle X}
x
{\displaystyle x}
P
(
X
>
x
)
{\displaystyle P(X>x)}
–ď—Ä–į—Ą–ł–ļ —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ–ĺ–Ļ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź
Φ ő¶ -->
{\displaystyle \Phi }
—Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—é –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ —ā–ĺ—á–ļ–ł (0;1/2), —ā–ĺ –Ķ—Ā—ā—Ć
Φ ő¶ -->
(
− ‚ąí -->
x
)
=
1
− ‚ąí -->
Φ ő¶ -->
(
x
)
.
{\displaystyle \Phi (-x)=1-\Phi (x).}
∫ ‚ąę -->
Φ ő¶ -->
(
x
)
d
x
=
x
Φ ő¶ -->
(
x
)
+
φ ŌÜ -->
(
x
)
+
C
.
{\displaystyle \int \Phi (x)\,dx=x\Phi (x)+\varphi (x)+C.}
–§—É–Ĺ–ļ—Ü–ł—Ź —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ–ĺ–Ļ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ļ —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć —Ä–į–∑–Ľ–ĺ–∂–Ķ–Ĺ–į —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é –ľ–Ķ—ā–ĺ–ī–į –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –Ņ–ĺ —á–į—Ā—ā—Ź–ľ –≤ —Ä—Ź–ī:
Φ ő¶ -->
(
x
)
=
1
2
+
1
2
π ŌÄ -->
⋅ ‚čÖ -->
e
− ‚ąí -->
x
2
/
2
[
x
+
x
3
3
+
x
5
3
⋅ ‚čÖ -->
5
+
⋯ ‚čĮ -->
+
x
2
n
+
1
(
2
n
+
1
)
!
!
+
⋯ ‚čĮ -->
]
,
{\displaystyle \Phi (x)={\frac {1}{2}}+{\frac {1}{\sqrt {2\pi }}}\cdot e^{-x^{2}/2}\left[x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{3\cdot 5}}+\cdots +{\frac {x^{2n+1}}{(2n+1)!!}}+\cdots \right],}
–≥–ī–Ķ –∑–Ĺ–į–ļ
!
!
{\displaystyle !!}
–ī–≤–ĺ–Ļ–Ĺ–ĺ–Ļ —Ą–į–ļ—ā–ĺ—Ä–ł–į–Ľ .
–ź—Ā–ł–ľ–Ņ—ā–ĺ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ —Ä–į–∑–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –ī–Ľ—Ź –Ī–ĺ–Ľ—Ć—ą–ł—Ö
x
{\displaystyle x}
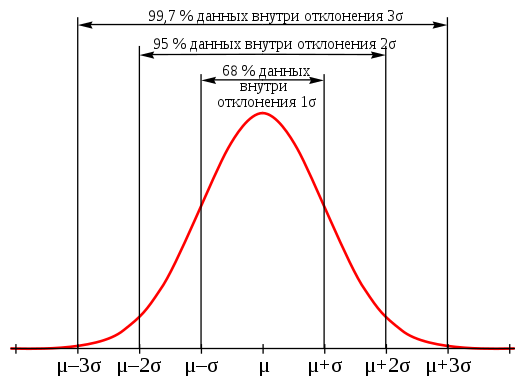
–ü—Ä–į–≤–ł–Ľ–ĺ 68-95-99,7. –ě–ļ–ĺ–Ľ–ĺ 68 % –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ļ –ł–∑ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –Ĺ–į—Ö–ĺ–ī—Ź—ā—Ā—Ź –Ĺ–į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł –Ĺ–Ķ –Ī–ĺ–Ľ–Ķ–Ķ –ĺ–ī–Ĺ–ĺ–≥–ĺ —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ–ĺ–≥–ĺ –ĺ—ā–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł—Ź ŌÉ –ĺ—ā —Ā—Ä–Ķ–ī–Ĺ–Ķ–≥–ĺ; –ĺ–ļ–ĺ–Ľ–ĺ 95 % –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ļ –Ľ–Ķ–∂–į—ā —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł –Ĺ–Ķ –Ī–ĺ–Ľ–Ķ–Ķ –ī–≤—É—Ö —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ—č—Ö –ĺ—ā–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł–Ļ; –ł 99,7 % –Ĺ–Ķ –Ī–ĺ–Ľ–Ķ–Ķ —ā—Ä—Ď—Ö. –≠—ā–ĺ—ā —Ą–į–ļ—ā —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —á–į—Ā—ā–Ĺ—č–ľ —Ā–Ľ—É—á–į–Ķ–ľ –Ņ—Ä–į–≤–ł–Ľ–į 3 —Ā–ł–≥–ľ –ī–Ľ—Ź –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ļ –≤—č–Ī–ĺ—Ä–ļ–ł.
–Ď–ĺ–Ľ–Ķ–Ķ —ā–ĺ—á–Ĺ–ĺ, –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā—Ć –Ņ–ĺ–Ľ—É—á–ł—ā—Ć –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ –≤ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–Ķ –ľ–Ķ–∂–ī—É
μ őľ -->
− ‚ąí -->
n
σ ŌÉ -->
{\displaystyle \mu -n\sigma }
μ őľ -->
+
n
σ ŌÉ -->
{\displaystyle \mu +n\sigma }
F
(
μ őľ -->
+
n
σ ŌÉ -->
)
− ‚ąí -->
F
(
μ őľ -->
− ‚ąí -->
n
σ ŌÉ -->
)
=
{\displaystyle F(\mu +n\sigma )-F(\mu -n\sigma )=}
Φ ő¶ -->
(
n
)
− ‚ąí -->
Φ ő¶ -->
(
− ‚ąí -->
n
)
=
erf
‚Ā° -->
(
n
2
)
.
{\displaystyle \Phi (n)-\Phi (-n)=\operatorname {erf} \left({\frac {n}{\sqrt {2}}}\right).}
–° —ā–ĺ—á–Ĺ–ĺ—Ā—ā—Ć—é –ī–ĺ 12 –∑–Ĺ–į—á–į—Č–ł—Ö —Ü–ł—Ą—Ä –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –ī–Ľ—Ź
n
=
1
,
2
,
… ‚Ķ -->
,
6
{\displaystyle n=1,2,\ldots ,6}
[ 8]
n
{\displaystyle n}
p
=
F
(
μ őľ -->
+
n
σ ŌÉ -->
)
− ‚ąí -->
F
(
μ őľ -->
− ‚ąí -->
n
σ ŌÉ -->
)
{\displaystyle p=F(\mu +n\sigma )-F(\mu -n\sigma )}
1
− ‚ąí -->
p
{\displaystyle 1-p}
1
1
− ‚ąí -->
p
{\displaystyle {\frac {1}{1-p}}}
OEIS
1
0,682689492137
0,317310507863
A178647
2
0,954499736104
0,045500263896
A110894
3
0,997300203937
0,002699796063
A270712
4
0,999936657516
0,000063342484
5
0,999999426697
0,000000573303
6
0,999999998027
0,000000001973
–ú–ĺ–ľ–Ķ–Ĺ—ā–į–ľ–ł –ł –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č–ľ–ł –ľ–ĺ–ľ–Ķ–Ĺ—ā–į–ľ–ł —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č
X
{\displaystyle X}
X
p
{\displaystyle X^{p}}
|
X
|
p
,
{\displaystyle \left|X\right|^{p},}
μ őľ -->
=
0
,
{\displaystyle \mu =0,}
—Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ—č–ľ–ł –ľ–ĺ–ľ–Ķ–Ĺ—ā–į–ľ–ł . –í –Ī–ĺ–Ľ—Ć—ą–ł–Ĺ—Ā—ā–≤–Ķ —Ā–Ľ—É—á–į–Ķ–≤ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—é—ā –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā –ľ–ĺ–ľ–Ķ–Ĺ—ā—č –ī–Ľ—Ź —Ü–Ķ–Ľ—č—Ö
p
.
{\displaystyle p.}
–ē—Ā–Ľ–ł
X
{\displaystyle X}
p
{\displaystyle p}
p
{\displaystyle p}
E
[
X
p
]
=
{
0
p
=
2
n
+
1
,
σ ŌÉ -->
p
(
p
− ‚ąí -->
1
)
!
!
p
=
2
n
.
{\displaystyle \mathbb {E} \left[X^{p}\right]={\begin{cases}0&p=2n+1,\\\sigma ^{p}\,\left(p-1\right)!!&p=2n.\end{cases}}}
–ó–ī–Ķ—Ā—Ć
n
{\displaystyle n}
(
p
− ‚ąí -->
1
)
!
!
{\displaystyle (p-1)!!}
–ī–≤–ĺ–Ļ–Ĺ–ĺ–Ļ —Ą–į–ļ—ā–ĺ—Ä–ł–į–Ľ —á–ł—Ā–Ľ–į
p
− ‚ąí -->
1
,
{\displaystyle p-1,}
p
− ‚ąí -->
1
{\displaystyle p-1}
1 –ī–ĺ
p
− ‚ąí -->
1.
{\displaystyle p-1.}
–¶–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ—č–Ķ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č–Ķ –ľ–ĺ–ľ–Ķ–Ĺ—ā—č –ī–Ľ—Ź –Ĺ–Ķ–ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —Ü–Ķ–Ľ—č—Ö
p
{\displaystyle p}
E
[
|
X
|
p
]
=
σ ŌÉ -->
p
(
p
− ‚ąí -->
1
)
!
!
⋅ ‚čÖ -->
{
2
π ŌÄ -->
p
=
2
n
+
1
,
1
p
=
2
n
.
}
=
σ ŌÉ -->
p
⋅ ‚čÖ -->
2
p
2
Γ őď -->
(
p
+
1
2
)
π ŌÄ -->
.
{\displaystyle \mathbb {E} \left[\left|X\right|^{p}\right]=\sigma ^{p}\,\left(p-1\right)!!\cdot \left.{\begin{cases}{\sqrt {\frac {2}{\pi }}}&p=2n+1,\\1&p=2n.\end{cases}}\right\}=\sigma ^{p}\cdot {\frac {2^{\frac {p}{2}}\Gamma \left({\frac {p+1}{2}}\right)}{\sqrt {\pi }}}.}
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ—Ź—Ź —Ą–ĺ—Ä–ľ—É–Ľ–į —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤–į —ā–į–ļ–∂–Ķ –ī–Ľ—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ—č—Ö
p
>
− ‚ąí -->
1
{\displaystyle p>-1}
–ü—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł–Ķ –§—É—Ä—Ć–Ķ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā–ł –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł
f
{\displaystyle f}
μ őľ -->
{\displaystyle \mu }
σ ŌÉ -->
{\displaystyle \sigma }
[ 9]
f
^ ^ -->
(
t
)
=
∫ ‚ąę -->
− ‚ąí -->
∞ ‚ąě -->
∞ ‚ąě -->
f
(
x
)
e
− ‚ąí -->
i
t
x
d
x
=
e
i
μ őľ -->
t
− ‚ąí -->
1
2
σ ŌÉ -->
2
t
2
,
{\displaystyle {\hat {f}}(t)=\int \limits _{-\infty }^{\infty }f(x)e^{-itx}\,dx=e^{i\mu t-{\frac {1}{2}}\sigma ^{2}t^{2}},}
–≥–ī–Ķ
i
{\displaystyle i}
–ľ–Ĺ–ł–ľ–į—Ź –Ķ–ī–ł–Ĺ–ł—Ü–į . –ē—Ā–Ľ–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –ĺ–∂–ł–ī–į–Ĺ–ł–Ķ
μ őľ -->
=
0
,
{\displaystyle \mu =0,}
1
/
σ ŌÉ -->
.
{\displaystyle 1/\sigma .}
φ ŌÜ -->
{\displaystyle \varphi }
—Ā–ĺ–Ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–į—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź –ĺ—ā –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł—Ź –§—É—Ä—Ć–Ķ.
–í —ā–Ķ–ĺ—Ä–ł–ł –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł, –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł–Ķ –§—É—Ä—Ć–Ķ –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā–ł —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č
X
{\displaystyle X}
—Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ
φ ŌÜ -->
X
(
t
)
{\displaystyle \varphi _{X}(t)}
–ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –ĺ–∂–ł–ī–į–Ĺ–ł–Ķ –ĺ—ā
e
i
t
X
{\displaystyle e^{itX}}
t
{\displaystyle t}
t
{\displaystyle t}
[ 10]
φ ŌÜ -->
X
(
t
)
=
f
^ ^ -->
(
− ‚ąí -->
t
)
.
{\displaystyle \varphi _{X}(t)={\hat {f}}(-t).}
–Ě–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –ī–Ķ–Ľ–ł–ľ—č–ľ .
–ē—Ā–Ľ–ł —Ā–Ľ—É—á–į–Ļ–Ĺ—č–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č
X
1
{\displaystyle X_{1}}
X
2
{\displaystyle X_{2}}
μ őľ -->
1
{\displaystyle \mu _{1}}
μ őľ -->
2
{\displaystyle \mu _{2}}
σ ŌÉ -->
1
2
{\displaystyle \sigma _{1}^{2}}
σ ŌÉ -->
2
2
{\displaystyle \sigma _{2}^{2}}
X
1
+
X
2
{\displaystyle X_{1}+X_{2}}
μ őľ -->
1
+
μ őľ -->
2
{\displaystyle \mu _{1}+\mu _{2}}
σ ŌÉ -->
1
2
+
σ ŌÉ -->
2
2
.
{\displaystyle \sigma _{1}^{2}+\sigma _{2}^{2}.}
–ě—ā—Ā—é–ī–į –≤—č—ā–Ķ–ļ–į–Ķ—ā, —á—ā–ĺ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–į—Ź —Ā–Ľ—É—á–į–Ļ–Ĺ–į—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł–ľ–į –ļ–į–ļ —Ā—É–ľ–ľ–į –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —á–ł—Ā–Ľ–į –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ—č—Ö –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ—č—Ö —Ā–Ľ—É—á–į–Ļ–Ĺ—č—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ.
–Ě–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –ł–ľ–Ķ–Ķ—ā –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ—É—é –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ—É—é —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—é —Ā—Ä–Ķ–ī–ł –≤—Ā–Ķ—Ö –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ—č—Ö —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ļ, –ī–ł—Ā–Ņ–Ķ—Ä—Ā–ł—Ź –ļ–ĺ—ā–ĺ—Ä—č—Ö –Ĺ–Ķ –Ņ—Ä–Ķ–≤—č—ą–į–Ķ—ā –∑–į–ī–į–Ĺ–Ĺ—É—é –≤–Ķ–Ľ–ł—á–ł–Ĺ—É[ 11] [ 12]
–ď—Ä–į—Ą–ł–ļ –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā–ł –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –ł –Ņ—Ä–ĺ—Ü–Ķ–Ĺ—ā –Ņ–ĺ–Ņ–į–ī–į–Ĺ–ł—Ź —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č –Ĺ–į –ĺ—ā—Ä–Ķ–∑–ļ–ł, —Ä–į–≤–Ĺ—č–Ķ —Ā—Ä–Ķ–ī–Ĺ–Ķ–ļ–≤–į–ī—Ä–į—ā–ł—á–Ķ—Ā–ļ–ĺ–ľ—É –ĺ—ā–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł—é. –ü—Ä–į–≤–ł–Ľ–ĺ —ā—Ä—Ď—Ö —Ā–ł–≥–ľ (
3
σ ŌÉ -->
{\displaystyle 3\sigma }
(
μ őľ -->
− ‚ąí -->
3
σ ŌÉ -->
;
μ őľ -->
+
3
σ ŌÉ -->
)
,
{\displaystyle \left(\mu -3\sigma ;\mu +3\sigma \right),}
–≥–ī–Ķ
μ őľ -->
=
E
ξ őĺ -->
{\displaystyle \mu =\mathbb {E} \xi }
–Ď–ĺ–Ľ–Ķ–Ķ —ā–ĺ—á–Ĺ–ĺ ‚ÄĒ –Ņ—Ä–ł–Ī–Ľ–ł–∑–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ —Ā –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā—Ć—é 0,9973 –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ–ĺ–Ļ —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č –Ľ–Ķ–∂–ł—ā –≤ —É–ļ–į–∑–į–Ĺ–Ĺ–ĺ–ľ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–Ķ.
–ü—Ä–ł –ļ–ĺ–ľ–Ņ—Ć—é—ā–Ķ—Ä–Ĺ–ĺ–ľ –ľ–ĺ–ī–Ķ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–ł–ł, –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–Ĺ–ĺ –Ņ—Ä–ł –Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–ł –ľ–Ķ—ā–ĺ–ī–į –ú–ĺ–Ĺ—ā–Ķ-–ö–į—Ä–Ľ–ĺ , –∂–Ķ–Ľ–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć –≤–Ķ–Ľ–ł—á–ł–Ĺ—č, —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–Ĺ—č–Ķ –Ņ–ĺ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–ľ—É –∑–į–ļ–ĺ–Ĺ—É. –ú–Ĺ–ĺ–≥–ł–Ķ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ—č –ī–į—é—ā —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ—č–Ķ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ—č–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č, —ā–į–ļ –ļ–į–ļ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ—É—é –≤–Ķ–Ľ–ł—á–ł–Ĺ—É
X
∼ ‚ąľ -->
N
(
μ őľ -->
,
σ ŌÉ -->
2
)
{\displaystyle X\sim N(\mu ,\sigma ^{2})}
X
=
μ őľ -->
+
σ ŌÉ -->
Z
,
{\displaystyle X=\mu +\sigma Z,}
–≥–ī–Ķ Z ‚ÄĒ —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ–į—Ź –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–į—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–į. –ź–Ľ–≥–ĺ—Ä–ł—ā–ľ—č —ā–į–ļ–∂–Ķ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—ā —Ä–į–∑–Ľ–ł—á–Ĺ—č–Ķ –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł—Ź —Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ—č—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ.
–ü—Ä–ĺ—Ā—ā–Ķ–Ļ—ą–ł–Ķ –Ņ—Ä–ł–Ī–Ľ–ł–∂—Ď–Ĺ–Ĺ—č–Ķ –ľ–Ķ—ā–ĺ–ī—č –ľ–ĺ–ī–Ķ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –ĺ—Ā–Ĺ–ĺ–≤—č–≤–į—é—ā—Ā—Ź –Ĺ–į —Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ—Ä–Ķ–ī–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ . –ē—Ā–Ľ–ł —Ā–Ľ–ĺ–∂–ł—ā—Ć –ī–ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ –Ī–ĺ–Ľ—Ć—ą–ĺ–Ķ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ—č—Ö –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—č—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ —Ā –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–Ļ –ī–ł—Ā–Ņ–Ķ—Ä—Ā–ł–Ķ–Ļ , —ā–ĺ —Ā—É–ľ–ľ–į –Ī—É–ī–Ķ—ā –ł–ľ–Ķ—ā—Ć —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ, –Ī–Ľ–ł–∑–ļ–ĺ–Ķ –ļ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–ľ—É. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ķ—Ā–Ľ–ł —Ā–Ľ–ĺ–∂–ł—ā—Ć 100 –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ—č—Ö —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ–ĺ —Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—č—Ö —Ā–Ľ—É—á–į–Ļ–Ĺ—č—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ, —ā–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —Ā—É–ľ–ľ—č –Ī—É–ī–Ķ—ā –Ņ—Ä–ł–Ī–Ľ–ł–∂—Ď–Ĺ–Ĺ–ĺ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ—č–ľ .
–Ē–Ľ—Ź –Ņ—Ä–ĺ–≥—Ä–į–ľ–ľ–Ĺ–ĺ–≥–ĺ –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—č—Ö –Ņ—Ā–Ķ–≤–ī–ĺ—Ā–Ľ—É—á–į–Ļ–Ĺ—č—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ –Ņ—Ä–Ķ–ī–Ņ–ĺ—á—ā–ł—ā–Ķ–Ľ—Ć–Ĺ–Ķ–Ķ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł–Ķ –Ď–ĺ–ļ—Ā–į ‚ÄĒ –ú—é–Ľ–Ľ–Ķ—Ä–į . –ě–Ĺ–ĺ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–ĺ–≤–į—ā—Ć –ĺ–ī–Ĺ—É –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—É—é –≤–Ķ–Ľ–ł—á–ł–Ĺ—É –Ĺ–į –Ī–į–∑–Ķ –ĺ–ī–Ĺ–ĺ–Ļ —Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ–ĺ–Ļ.
–Ę–į–ļ–∂–Ķ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –į–Ľ–≥–ĺ—Ä–ł—ā–ľ –ó–ł–ļ–ļ—É—Ä–į—ā , –ļ–ĺ—ā–ĺ—Ä—č–Ļ —Ä–į–Ī–ĺ—ā–į–Ķ—ā –ī–į–∂–Ķ –Ī—č—Ā—ā—Ä–Ķ–Ķ –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł—Ź –Ď–ĺ–ļ—Ā–į ‚ÄĒ –ú—é–Ľ–Ľ–Ķ—Ä–į. –ě–Ĺ —Ā–Ľ–ĺ–∂–Ĺ–Ķ–Ķ –≤ —Ä–Ķ–į–Ľ–ł–∑–į—Ü–ł–ł, –Ĺ–ĺ –Ķ–≥–ĺ –Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ –ĺ–Ņ—Ä–į–≤–ī–į–Ĺ–ĺ –≤ —Ā–Ľ—É—á–į—Ź—Ö, –ļ–ĺ–≥–ī–į —ā—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–ĺ–≤–į–Ĺ–ł–Ķ –ĺ—á–Ķ–Ĺ—Ć –Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ —á–ł—Ā–Ľ–į –Ĺ–Ķ—Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—č—Ö —Ā–Ľ—É—á–į–Ļ–Ĺ—č—Ö —á–ł—Ā–Ķ–Ľ.
–Ě–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —á–į—Ā—ā–ĺ –≤—Ā—ā—Ä–Ķ—á–į–Ķ—ā—Ā—Ź –≤ –Ņ—Ä–ł—Ä–ĺ–ī–Ķ. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, —Ā–Ľ–Ķ–ī—É—é—Č–ł–Ķ —Ā–Ľ—É—á–į–Ļ–Ĺ—č–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č —Ö–ĺ—Ä–ĺ—ą–ĺ –ľ–ĺ–ī–Ķ–Ľ–ł—Ä—É—é—ā—Ā—Ź –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ—č–ľ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ–ľ:
–ĺ—ā–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ł —Ā—ā—Ä–Ķ–Ľ—Ć–Ī–Ķ;
–Ņ–ĺ–≥—Ä–Ķ—ą–Ĺ–ĺ—Ā—ā–ł –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł–Ļ (–ĺ–ī–Ĺ–į–ļ–ĺ –Ņ–ĺ–≥—Ä–Ķ—ą–Ĺ–ĺ—Ā—ā–ł –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č—Ö –ł–∑–ľ–Ķ—Ä–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –Ņ—Ä–ł–Ī–ĺ—Ä–ĺ–≤ –ł–ľ–Ķ—é—ā –ł–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ);–Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ķ —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ–ł –∂–ł–≤—č—Ö –ĺ—Ä–≥–į–Ĺ–ł–∑–ľ–ĺ–≤ –≤ –Ņ–ĺ–Ņ—É–Ľ—Ź—Ü–ł–ł. –Ę–į–ļ–ĺ–Ķ —ą–ł—Ä–ĺ–ļ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ–Ķ–Ĺ–ł–Ķ —ć—ā–ĺ–≥–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź —Ā–≤—Ź–∑–į–Ĺ–ĺ —Ā —ā–Ķ–ľ, —á—ā–ĺ –ĺ–Ĺ–ĺ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –ī–Ķ–Ľ–ł–ľ—č–ľ –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ—č–ľ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ–ľ —Ā –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–Ļ –ī–ł—Ā–Ņ–Ķ—Ä—Ā–ł–Ķ–Ļ. –ü–ĺ—ć—ā–ĺ–ľ—É –ļ –Ĺ–Ķ–ľ—É –≤ –Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ –Ņ—Ä–ł–Ī–Ľ–ł–∂–į—é—ā—Ā—Ź –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ķ –ī—Ä—É–≥–ł–Ķ, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä –Ī–ł–Ĺ–ĺ–ľ–ł–į–Ľ—Ć–Ĺ–ĺ–Ķ –ł –Ņ—É–į—Ā—Ā–ĺ–Ĺ–ĺ–≤—Ā–ļ–ĺ–Ķ . –≠—ā–ł–ľ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ–ľ –ľ–ĺ–ī–Ķ–Ľ–ł—Ä—É—é—ā—Ā—Ź –ľ–Ĺ–ĺ–≥–ł–Ķ –Ĺ–Ķ–ī–Ķ—ā–Ķ—Ä–ľ–ł–Ĺ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č–Ķ —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ķ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā—č[ 13]
–ú–Ĺ–ĺ–≥–ĺ–ľ–Ķ—Ä–Ĺ–ĺ–Ķ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –Ņ—Ä–ł –ł—Ā—Ā–Ľ–Ķ–ī–ĺ–≤–į–Ĺ–ł–ł –ľ–Ĺ–ĺ–≥–ĺ–ľ–Ķ—Ä–Ĺ—č—Ö —Ā–Ľ—É—á–į–Ļ–Ĺ—č—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ (—Ā–Ľ—É—á–į–Ļ–Ĺ—č—Ö –≤–Ķ–ļ—ā–ĺ—Ä–ĺ–≤). –ě–ī–Ĺ–ł–ľ –ł–∑ –ľ–Ĺ–ĺ–≥–ĺ—á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ—č—Ö –Ņ—Ä–ł–ľ–Ķ—Ä–ĺ–≤ —ā–į–ļ–ł—Ö –Ņ—Ä–ł–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ļ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ł—Ā—Ā–Ľ–Ķ–ī–ĺ–≤–į–Ĺ–ł–Ķ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ĺ–≤ –Ľ–ł—á–Ĺ–ĺ—Ā—ā–ł —á–Ķ–Ľ–ĺ–≤–Ķ–ļ–į –≤ –Ņ—Ā–ł—Ö–ĺ–Ľ–ĺ–≥–ł–ł –ł –Ņ—Ā–ł—Ö–ł–į—ā—Ä–ł–ł .
–Ě–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ–ľ –ü–ł—Ä—Ā–ĺ–Ĺ–į —ā–ł–Ņ–į XI[ 14]
–ě—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ –Ņ–į—Ä—č –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ—č—Ö —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ—č—Ö –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–Ĺ—č—Ö —Ā–Ľ—É—á–į–Ļ–Ĺ—č—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ –ł–ľ–Ķ–Ķ—ā —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –ö–ĺ—ą–ł [ 15]
X
{\displaystyle X}
X
=
Y
/
Z
{\displaystyle X=Y/Z}
Y
{\displaystyle Y}
Z
{\displaystyle Z}
–ē—Ā–Ľ–ł
z
1
,
… ‚Ķ -->
,
z
k
{\displaystyle z_{1},\ldots ,z_{k}}
z
i
∼ ‚ąľ -->
N
(
0
,
1
)
,
{\displaystyle z_{i}\sim N\left(0,1\right),}
x
=
z
1
2
+
… ‚Ķ -->
+
z
k
2
{\displaystyle x=z_{1}^{2}+\ldots +z_{k}^{2}}
—Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —Ö–ł-–ļ–≤–į–ī—Ä–į—ā —Ā k
–ē—Ā–Ľ–ł —Ā–Ľ—É—á–į–Ļ–Ĺ–į—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–į
X
{\displaystyle X}
–Ľ–ĺ–≥–Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–ľ—É —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é , —ā–ĺ –Ķ—Ď –Ĺ–į—ā—É—Ä–į–Ľ—Ć–Ĺ—č–Ļ –Ľ–ĺ–≥–į—Ä–ł—Ą–ľ –ł–ľ–Ķ–Ķ—ā –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ. –Ę–ĺ –Ķ—Ā—ā—Ć, –Ķ—Ā–Ľ–ł
X
∼ ‚ąľ -->
L
o
g
N
(
μ őľ -->
,
σ ŌÉ -->
2
)
,
{\displaystyle X\sim \mathrm {LogN} \left(\mu ,\sigma ^{2}\right),}
Y
=
ln
‚Ā° -->
(
X
)
∼ ‚ąľ -->
N
(
μ őľ -->
,
σ ŌÉ -->
2
)
.
{\displaystyle Y=\ln \left(X\right)\sim \mathrm {N} \left(\mu ,\sigma ^{2}\right).}
Y
∼ ‚ąľ -->
N
(
μ őľ -->
,
σ ŌÉ -->
2
)
,
{\displaystyle Y\sim \mathrm {N} \left(\mu ,\sigma ^{2}\right),}
X
=
exp
‚Ā° -->
(
Y
)
∼ ‚ąľ -->
L
o
g
N
(
μ őľ -->
,
σ ŌÉ -->
2
)
.
{\displaystyle X=\exp \left(Y\right)\sim \mathrm {LogN} \left(\mu ,\sigma ^{2}\right).}
–ē—Ā–Ľ–ł
X
1
,
X
2
,
.
.
.
,
X
n
{\displaystyle X_{1},X_{2},...,X_{n}}
μ őľ -->
{\displaystyle \mu }
σ ŌÉ -->
2
,
{\displaystyle \sigma ^{2},}
–≤—č–Ī–ĺ—Ä–ĺ—á–Ĺ–ĺ–Ķ —Ā—Ä–Ķ–ī–Ĺ–Ķ–Ķ –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ –ĺ—ā –≤—č–Ī–ĺ—Ä–ĺ—á–Ĺ–ĺ–≥–ĺ —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ–ĺ–≥–ĺ –ĺ—ā–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł—Ź [ 16] t-—Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —Ā
n
− ‚ąí -->
1
{\displaystyle {\text{n}}-1}
t
=
X
¯ ¬Į -->
− ‚ąí -->
μ őľ -->
S
/
n
=
1
n
(
X
1
+
⋯ ‚čĮ -->
+
X
n
)
− ‚ąí -->
μ őľ -->
1
n
(
n
− ‚ąí -->
1
)
[
(
X
1
− ‚ąí -->
X
¯ ¬Į -->
)
2
+
⋯ ‚čĮ -->
+
(
X
n
− ‚ąí -->
X
¯ ¬Į -->
)
2
]
∼ ‚ąľ -->
t
n
− ‚ąí -->
1
.
{\displaystyle t={\frac {{\overline {X}}-\mu }{S/{\sqrt {n}}}}={\frac {{\frac {1}{n}}(X_{1}+\cdots +X_{n})-\mu }{\sqrt {{\frac {1}{n(n-1)}}\left[(X_{1}-{\overline {X}})^{2}+\cdots +(X_{n}-{\overline {X}})^{2}\right]}}}\sim t_{n-1}.}
–ē—Ā–Ľ–ł
X
1
,
X
2
,
.
.
.
,
X
n
,
{\displaystyle X_{1},X_{2},...,X_{n},}
Y
1
,
Y
2
,
.
.
.
,
Y
n
{\displaystyle Y_{1},Y_{2},...,Y_{n}}
—Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –§–ł—ą–Ķ—Ä–į —Ā (
n
,
{\displaystyle {\text{n}},}
m
{\displaystyle {\text{m}}}
[ 17]
F
=
(
X
1
2
+
X
2
2
+
⋯ ‚čĮ -->
+
X
n
2
)
/
n
(
Y
1
2
+
Y
2
2
+
⋯ ‚čĮ -->
+
Y
m
2
)
/
m
∼ ‚ąľ -->
F
n
,
m
.
{\displaystyle F={\frac {\left(X_{1}^{2}+X_{2}^{2}+\cdots +X_{n}^{2}\right)/n}{\left(Y_{1}^{2}+Y_{2}^{2}+\cdots +Y_{m}^{2}\right)/m}}\sim F_{n,m}.}
–ě—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ –ļ–≤–į–ī—Ä–į—ā–ĺ–≤ –ī–≤—É—Ö —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ—č—Ö –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ—č—Ö —Ā–Ľ—É—á–į–Ļ–Ĺ—č—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ –ł–ľ–Ķ–Ķ—ā —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –§–ł—ą–Ķ—Ä–į —Ā–ĺ —Ā—ā–Ķ–Ņ–Ķ–Ĺ—Ź–ľ–ł —Ā–≤–ĺ–Ī–ĺ–ī—č
(
1
,
1
)
.
{\displaystyle \left(1,1\right).}
–í–Ņ–Ķ—Ä–≤—č–Ķ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –ļ–į–ļ –Ņ—Ä–Ķ–ī–Ķ–Ľ –Ī–ł–Ĺ–ĺ–ľ–ł–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –Ņ—Ä–ł
p
=
1
2
{\displaystyle p={\tfrac {1}{2}}}
–ú—É–į–≤—Ä–į ¬ę–Ē–ĺ–ļ—ā—Ä–ł–Ĺ–į —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ—Ā—ā–Ķ–Ļ¬Ľ [–į–Ĺ–≥–Ľ.] [ 18] —Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ—Ä–Ķ–ī–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —ā–Ķ–ĺ—Ä–Ķ–ľ—č . –í 1809 –≥–ĺ–ī—É –ď–į—É—Ā—Ā –≤ —Ā–ĺ—á–ł–Ĺ–Ķ–Ĺ–ł–ł ¬ę–Ę–Ķ–ĺ—Ä–ł—Ź –ī–≤–ł–∂–Ķ–Ĺ–ł—Ź –Ĺ–Ķ–Ī–Ķ—Ā–Ĺ—č—Ö —ā–Ķ–Ľ¬Ľ –≤–≤—Ď–Ľ —ć—ā–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –ļ–į–ļ –≤–ĺ–∑–Ĺ–ł–ļ–į—é—Č–Ķ–Ķ –≤ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–Ķ –ľ–Ĺ–ĺ–≥–ĺ–ļ—Ä–į—ā–Ĺ—č—Ö –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł–Ļ –ī–≤–ł–∂–Ķ–Ĺ–ł—Ź –Ĺ–Ķ–Ī–Ķ—Ā–Ĺ—č—Ö —ā–Ķ–Ľ. –ě–ī–Ĺ–į–ļ–ĺ –ď–į—É—Ā—Ā –≤—č–≤–Ķ–Ľ —Ą–ĺ—Ä–ľ—É–Ľ—É –ī–Ľ—Ź –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —Ā–Ľ—É—á–į–Ļ–Ĺ—č—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ –ł–∑ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į –ī–ĺ—Ā—ā–ł–∂–Ķ–Ĺ–ł—Ź –ľ–į–ļ—Ā–ł–ľ—É–ľ–į —Ā–ĺ–≤–ľ–Ķ—Ā—ā–Ĺ–ĺ–Ļ –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā–ł –≤—Ā–Ķ—Ö –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł–Ļ –≤ —ā–ĺ—á–ļ–Ķ —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į–ľ–ł, —Ä–į–≤–Ĺ—č–ľ–ł —Ā—Ä–Ķ–ī–Ĺ–Ķ–ľ—É –≤—Ā–Ķ—Ö –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł–Ļ. –≠—ā–ĺ—ā –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –≤–Ņ–ĺ—Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–ł –Ņ–ĺ–ī–≤–Ķ—Ä–≥–į–Ľ—Ā—Ź –ļ—Ä–ł—ā–ł–ļ–Ķ. –í 1812 –≥–ĺ–ī—É –õ–į–Ņ–Ľ–į—Ā –≤ —ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –ú—É–į–≤—Ä–į ‚ÄĒ –õ–į–Ņ–Ľ–į—Ā–į –ĺ–Ī–ĺ–Ī—Č–ł–Ľ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā –ú—É–į–≤—Ä–į –ī–Ľ—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ –Ī–ł–Ĺ–ĺ–ľ–ł–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź, —ā–ĺ –Ķ—Ā—ā—Ć –ī–Ľ—Ź —Ā—É–ľ–ľ –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—č—Ö –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ—č—Ö –Ī–ł–Ĺ–į—Ä–Ĺ—č—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ[ 3]
‚ÜĎ –í–Ķ–Ĺ—ā—Ü–Ķ–Ľ—Ć –ē. –°. –ú. : Academia , 2005. ‚ÄĒ 576 —Ā. ‚ÄĒ ISBN 5-7695-2311-5 .‚ÜĎ –®–ł—Ä—Ź–Ķ–≤ –ź. –Ě. –ú. : –Ě–į—É–ļ–į, 1980.‚ÜĎ 1 2 –ú–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–Ļ —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–Ľ–ĺ–≤–į—Ä—Ć . ‚ÄĒ –ú. : –°–ĺ–≤–Ķ—ā—Ā–ļ–į—Ź —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź , 1988. ‚ÄĒ –°. 139 ‚ÄĒ140.‚ÜĎ Wasserman L. All of Statistics . ‚ÄĒ New York, NY: Springer, 2004. ‚ÄĒ –°. 142 . ‚ÄĒ 433 —Ā. ‚ÄĒ ISBN 978-1-4419-2322-6 .‚ÜĎ –Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ —Ā–ľ. –ď–į—É—Ā—Ā–ĺ–≤ –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ
‚ÜĎ Halperin, Hartley & Hoel, 1965 , item 7.‚ÜĎ McPherson (1990) harvtxt error: —Ź–ļ–ĺ—Ä—Ź –Ĺ–Ķ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā: CITEREFMcPherson1990 (–Ņ–ĺ–ľ–ĺ—Č—Ć ) ‚ÜĎ Wolfram|Alpha: Computational Knowledge Engine (–Ĺ–Ķ–ĺ–Ņ—Ä.) . Wolframalpha.com . –Ē–į—ā–į –ĺ–Ī—Ä–į—Č–Ķ–Ĺ–ł—Ź: 3 –ľ–į—Ä—ā–į 2017.‚ÜĎ Bryc (1995 , p. 23) harvtxt error: —Ź–ļ–ĺ—Ä—Ź –Ĺ–Ķ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā: CITEREFBryc1995 (–Ņ–ĺ–ľ–ĺ—Č—Ć ) ‚ÜĎ Bryc (1995 , p. 24) harvtxt error: —Ź–ļ–ĺ—Ä—Ź –Ĺ–Ķ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā: CITEREFBryc1995 (–Ņ–ĺ–ľ–ĺ—Č—Ć ) ‚ÜĎ Cover, Thomas M.; Thomas, Joy A. Elements of Information Theory. ‚ÄĒ John Wiley and Sons , 2006. ‚ÄĒ –°. 254.‚ÜĎ Park, Sung Y.; Bera, Anil K. Maximum Entropy Autoregressive Conditional Heteroskedasticity Model (–į–Ĺ–≥–Ľ.) // Journal of Econometrics [–į–Ĺ–≥–Ľ.] P. 219‚ÄĒ230 . –ź—Ä—Ö–ł–≤–ł—Ä–ĺ–≤–į–Ĺ–ĺ 7 –ľ–į—Ä—ā–į 2016 –≥–ĺ–ī–į.‚ÜĎ –Ę–į–Ľ–Ķ–Ī –Ě. –Ě. –ß—Ď—Ä–Ĺ—č–Ļ –Ľ–Ķ–Ī–Ķ–ī—Ć. –ü–ĺ–ī –∑–Ĺ–į–ļ–ĺ–ľ –Ĺ–Ķ–Ņ—Ä–Ķ–ī—Ā–ļ–į–∑—É–Ķ–ľ–ĺ—Ā—ā–ł = The Black Swan: The Impact of the Highly Improbable. ‚ÄĒ –ö–ĺ–õ–ł–Ī—Ä–ł, 2012. ‚ÄĒ 525 —Ā. ‚ÄĒ ISBN 978-5-389-00573-0 .‚ÜĎ –ö–ĺ—Ä–ĺ–Ľ—é–ļ, 1985 , —Ā. 135.‚ÜĎ –ď–į–Ľ–ļ–ł–Ĺ –í. –ú., –ē—Ä–ĺ—Ą–Ķ–Ķ–≤–į –õ. –Ě., –õ–Ķ—Č–Ķ–≤–į –°. –í. –ě—Ü–Ķ–Ĺ–ļ–ł –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–į —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –ö–ĺ—ą–ł : [–į—Ä—Ö. 30 –ł—é–Ľ—Ź 2017–Ě–ł–∂–Ķ–≥–ĺ—Ä–ĺ–ī—Ā–ļ–ĺ–≥–ĺ –≥–ĺ—Ā—É–ī–į—Ä—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —É–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –ł–ľ. –†. –ē. –ź–Ľ–Ķ–ļ—Ā–Ķ–Ķ–≤–į . ‚ÄĒ 2014. ‚ÄĒ ‚ĄĖ 2(104). ‚ÄĒ –°. 314‚ÄĒ319. ‚ÄĒ –£–Ē–ö 513.015.2(G) ‚ÜĎ Lukacs, Eugene. A Characterization of the Normal Distribution (–į–Ĺ–≥–Ľ.) // The Annals of Mathematical Statistics [–į–Ĺ–≥–Ľ.] Vol. 13 , no. 1 . ‚ÄĒ P. 91‚ÄĒ3 . ‚ÄĒ ISSN 0003-4851 . ‚ÄĒ doi :10.1214/aoms/1177731647 . ‚ÄĒ JSTOR 2236166 ‚ÜĎ Lehmann, E. L. [–į–Ĺ–≥–Ľ.] Testing Statistical Hypotheses . ‚ÄĒ 2nd. ‚ÄĒ Springer [–į–Ĺ–≥–Ľ.] 199 . ‚ÄĒ ISBN 978-0-387-94919-2 .‚ÜĎ The doctrine of chances; or, a method of calculating the probability of events in play, L., 1718, 1738, 1756; L., 1967 (—Ä–Ķ–Ņ—Ä–ĺ–ī—É—Ü–ł—Ä. –ł–∑–ī.); Miscellanea analytica de scriebus et quadraturis, L., 1730.
–ö–ĺ—Ä–ĺ–Ľ—é–ļ –í. –°. , –ü–ĺ—Ä—ā–Ķ–Ĺ–ļ–ĺ –Ě. –ė. , –°–ļ–ĺ—Ä–ĺ—Ö–ĺ–ī –ź. –í. , –Ę—É—Ä–Ī–ł–Ĺ –ź. –§. –ú. : –Ě–į—É–ļ–į, 1985. ‚ÄĒ 640 —Ā.Halperin, Max; Hartley, Herman O.; Hoel, Paul G. Recommended Standards for Statistical Symbols and Notation. COPSS Committee on Symbols and Notation (–į–Ĺ–≥–Ľ.) // The American Statistician [–į–Ĺ–≥–Ľ.] Vol. 19 , no. 3 . ‚ÄĒ P. 12‚ÄĒ14 . ‚ÄĒ doi :10.2307/2681417 . ‚ÄĒ JSTOR 2681417 McPherson, Glen. Statistics in Scientific Investigation: Its Basis, Application and Interpretation (–į–Ĺ–≥–Ľ.) . ‚ÄĒ Springer-Verlag , 1990. ‚ÄĒ ISBN 978-0-387-97137-7 .Bryc, Wlodzimierz. The Normal Distribution: Characterizations with Applications (–į–Ĺ–≥–Ľ.) . ‚ÄĒ Springer-Verlag , 1995. ‚ÄĒ ISBN 978-0-387-97990-8 .
–°—Ā—č–Ľ–ļ–ł –Ĺ–į –≤–Ĺ–Ķ—ą–Ĺ–ł–Ķ —Ä–Ķ—Ā—É—Ä—Ā—č
–Ę–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–Ķ —Ā–į–Ļ—ā—č
–°–Ľ–ĺ–≤–į—Ä–ł –ł —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł–ł –í –Ī–ł–Ī–Ľ–ł–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł—Ö –ļ–į—ā–į–Ľ–ĺ–≥–į—Ö
–Ē–ł—Ā–ļ—Ä–Ķ—ā–Ĺ—č–Ķ –ź–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ
























![{\displaystyle \Phi ({\frac {x-\mu }{\sigma }})={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sqrt {2\sigma ^{2}}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e6761619c13b85e117f8cf8aa6dbc7b4ec9554e)














































![{\displaystyle [-x,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e23c41ff0bd6f01a0e27054c2b85819fcd08b762)

![{\displaystyle \Phi (x)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7831a9a5f630df7170fa805c186f4c53219ca36)

![{\displaystyle F(x)=\Phi \left({\frac {x-\mu }{\sigma }}\right)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a75caa2df3861960f6c6a5ac91f0b0fa6d79504)





![{\displaystyle \Phi (x)={\frac {1}{2}}+{\frac {1}{\sqrt {2\pi }}}\cdot e^{-x^{2}/2}\left[x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{3\cdot 5}}+\cdots +{\frac {x^{2n+1}}{(2n+1)!!}}+\cdots \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b755fcac449fe404b290943b01b01eab9c50440a)















![{\displaystyle \mathbb {E} \left[X^{p}\right]={\begin{cases}0&p=2n+1,\\\sigma ^{p}\,\left(p-1\right)!!&p=2n.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c39f9a1d5eadfbc872b3cd41f8135576e3123bc4)




![{\displaystyle \mathbb {E} \left[\left|X\right|^{p}\right]=\sigma ^{p}\,\left(p-1\right)!!\cdot \left.{\begin{cases}{\sqrt {\frac {2}{\pi }}}&p=2n+1,\\1&p=2n.\end{cases}}\right\}=\sigma ^{p}\cdot {\frac {2^{\frac {p}{2}}\Gamma \left({\frac {p+1}{2}}\right)}{\sqrt {\pi }}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c45215d47f1e0fc958abfae9a8d7137995cf90a8)



































![{\displaystyle t={\frac {{\overline {X}}-\mu }{S/{\sqrt {n}}}}={\frac {{\frac {1}{n}}(X_{1}+\cdots +X_{n})-\mu }{\sqrt {{\frac {1}{n(n-1)}}\left[(X_{1}-{\overline {X}})^{2}+\cdots +(X_{n}-{\overline {X}})^{2}\right]}}}\sim t_{n-1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36ff0d3c79a0504e8f259ef99192b825357914d7)






