Наибольшее известное простое число
|
Read other articles:

Danijel Ljuboja Di Legia Warsaw, 2011Informasi pribadiNama lengkap Danijel LjubojaTanggal lahir 04 September 1978 (umur 45)Tempat lahir Vinkovci, YugoslaviaTinggi 1,89 m (6 ft 2+1⁄2 in)Posisi bermain PenyerangKarier junior NK Dinamo Vinkovci NK Osijek Red Star Belgrade SochauxKarier senior*Tahun Tim Tampil (Gol)1998–2000 Sochaux 62 (20)2000–2004 Strasbourg 123 (34)2004–2006 Paris Saint-Germain 42 (7)2005–2006 VfB Stuttgart (pinjam) 26 (8)2006–2009 VfB Stut...

Kodok laut Chaunacops melanostomus Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Animalia Filum: Chordata Kelas: Actinopterygii Ordo: Lophiiformes Subordo: Chaunacoidei Famili: ChaunacidaeGill, 1863 Genus[1] Chaunacops Chaunax Chaunacidae adalah ikan dalam ordo lophiiformes yang dikenal sebagai Kodok laut.[2] Ikan ini adalah ikan yang hidup di dasar laut yang ditemukan di lereng benua Samudra Atlantik, Hindia, dan Pasifik,[3] pada kedalaman setidaknya 2.460 m. Ada ju...

Keong macan Babylonia spirata TaksonomiKerajaanAnimaliaFilumMolluscaKelasGastropodaOrdoNeogastropodaFamiliBabyloniidaeGenusBabyloniaSpesiesBabylonia spirata Linnaeus, 1758 lbs Babilonia spirata, atau nama umumnya keong macan adalah spesies siput laut, moluska gastropoda laut, dalam keluarga Babyloniidae . [1] Ini adalah jenis spesies dari genus Babilonia . [2]Cangkangnya sering dijadikan sebagai cenderamata atau sekadar pernak-pernik. Babilonia spirata mirip dengan B. zeylanic...

George AkerlofLahirGeorge Arthur Akerlof17 Juni 1940 (umur 83)New Haven, ConnecticutKebangsaanUnited StatesInstitusiUniversity of California, BerkeleyMazhabNew Keynesian economicsAlma materMIT (Ph.D.)Yale University (B.A.)DipengaruhiRobert SolowKontribusiInformation asymmetryEfficiency wagesPenghargaanNobel Prize in Economics (2001)Informasi di IDEAS / RePEc George Arthur Akerlof (lahir 17 Juni 1940 di New Haven, Connecticut) ialah ekonom Amerika Serikat. Akerlof menerima...

العلاقات الصينية الكندية الصين كندا تعديل مصدري - تعديل تعود العلاقات الصينية الكندية بشكل رسمي إلى عام 1942 عندما أرسلت كندا سفيرًا لها إلى الصين. مُثِّلت كندا قبل ذلك بالسفير البريطاني. تسبب الانتصار الشيوعي (1949) في الحرب الأهلية الصينية في انقطاع العل...
Capacité thermique La grande capacité thermique massique de l'eau donne à la bouillotte une grande capacité thermique sous un volume raisonnable.Données clés Unités SI joule par kelvin (J K−1) Dimension M·L 2·T −2·Θ −1 Nature Grandeur scalaire extensive Symbole usuel C X {\displaystyle C_{X}} à X {\displaystyle X} constant Lien à d'autres grandeurs C X = T ( ∂ S ∂ T ) X {\displaystyle C_{X}=T\left({\partial S \over \partial T}\right)...

1971 studio album by ChainToward the BluesStudio album by ChainReleased1971StudioT.C.S. Studios (Melbourne)GenreBluesLength42:38LabelInfinity RecordsProducerChain and John SayersChain chronology Chain Live(1970) Toward the Blues(1971) Live Again(1972) Toward the Blues is a studio album by the Australian blues band Chain which reached No. 6 on the Kent Music Report albums chart.[1] In October 2010, it was listed in the book, 100 Best Australian Albums.[2] The 30th anni...

Questa voce sull'argomento calciatori emiratini è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Zuhair Bakhit Bilal Nazionalità Emirati Arabi Uniti Calcio Ruolo Attaccante Carriera Squadre di club1 1988-2004 Al-Wasl? (?) Nazionale 1988-2002 Emirati Arabi Uniti112 (27) Palmarès Coppa d'Asia Argento Emirati Arabi Uniti 1996 1 I due numeri indicano le presenze e le reti segnate, per le ...

Bupati Kabupaten Minahasa TenggaraPetahanaRonald Sorongan (Pj.)sejak 25 September 2023Masa jabatanLima tahunDibentuk2007Pejabat pertamaTelly TjanggulungSitus webmitrakab.go.id Berikut ini adalah daftar bupati Minahasa Tenggara yang menjabat sejak pembentukannya pada tahun 2007. No. Foto Nama Mulai jabatan Akhir jabatan Prd. Wakil Bupati Ket. 1 Telly Tjanggulung 24 September 2008 2013 1 Drs.Jeremia Damongilala [1] 2 James SumendapS.H. 24 September 2013 25 September 2018 2 Ronald K...

Russian poet, critic, publisher (1821–1878) For other uses, see Nikolai Nekrasov (disambiguation). In this name that follows Eastern Slavic naming customs, the patronymic is Alexeyevich and the family name is Nekrasov. Nikolay NekrasovNekrasov in 1870BornNikolay Alexeyevich Nekrasov10 December [O.S. 28 November] 1821[1]Nemyriv, Bratslavsky Uyezd, Podolia Governorate, Russian Empire[1]Died8 January 1878 [O.S. 27 December 1877] (aged 56)[1&#...

American actress (1926–2005) June HaverHaver in 1947BornBeverly June Stovenour(1926-06-10)June 10, 1926Rock Island, Illinois, U.S.DiedJuly 4, 2005(2005-07-04) (aged 79)Los Angeles, California, U.S.OccupationsActresssingerdancerYears active1941–1953Known forWhere Do We Go from Here?The Dolly SistersIrish Eyes Are SmilingWake Up and DreamThree Little Girls in BlueSpouses Jimmy Zito (m. 1947; div. 1948) Fred MacMurray ...

مايكروسوفت فورفرونتمعلومات عامةنوع مجموعة برمجيات أمن الحاسوبموقع الويب microsoft.com… تعديل - تعديل مصدري - تعديل ويكي بيانات مايكروسوفت فورفرونت (بالإنجليزية: Microsoft Forefront) هي مجموعة برمجيات أمن الحاسوب طوَّرتها شركة مايكروسوفت، مُوَّجهة خصيصًا لشبكات الحاسوب أو الخوادم.[...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Armaan...

In & OutJoan Cusack e Kevin Kline in una scena del filmPaese di produzioneStati Uniti d'America Anno1997 Durata90 min Generecommedia RegiaFrank Oz SceneggiaturaPaul Rudnick FotografiaRob Hahn MontaggioDan Hanley, John Jympson MusicheMarc Shaiman ScenografiaKen Adam CostumiAnn Roth Interpreti e personaggi Kevin Kline: Howard Brackett Joan Cusack: Emily Montgomery Tom Selleck: Peter Malloy Matt Dillon: Cameron Drake Debbie Reynolds: Berniece Brackett Wilford Brimley: Frank Brackett Bob Newh...

Kate WinsletKate Winslet di Festival Film Internasional Toronto 2017LahirKate Elizabeth Winslet5 Oktober 1975 (umur 48)Reading, Berkshire, InggrisPekerjaanAktris • PenyanyiTahun aktif1991 – sekarangSuami/istriJim Threapleton(1998—2001) Sam Mendes(2003—2010)Ned Rock 'n Roll (2012-sekarang) Kate Elizabeth Winslet (lahir 5 Oktober 1975) merupakan seorang aktris berkebangsaan Inggris. Dia merupakan pemenang Academy Award, Emmy Award, BAFTA, Grammy Award, dan Screen Actors Guild...

Mazda RX-8InformasiProdusenMazdaMasa produksi2003-2011 [1][2]PerakitanHiroshima, JapanBodi & rangkaKelasMobil sportBentuk kerangka4-door quad coupéTata letakFMR layoutMobil terkaitMazda MX-5 (3rd generation)Penyalur dayaMesin1.3 L RENESIS (Wankel) NATransmisi4-speed automatic6-speed automatic 5-speed manual6-speed manualDimensiJarak sumbu roda2.703 mm (106,4 in)Panjang2004–08: 4.425 mm (174,2 in)2009–: 4.470 mm (176,0 in)Lebar1.770&#...
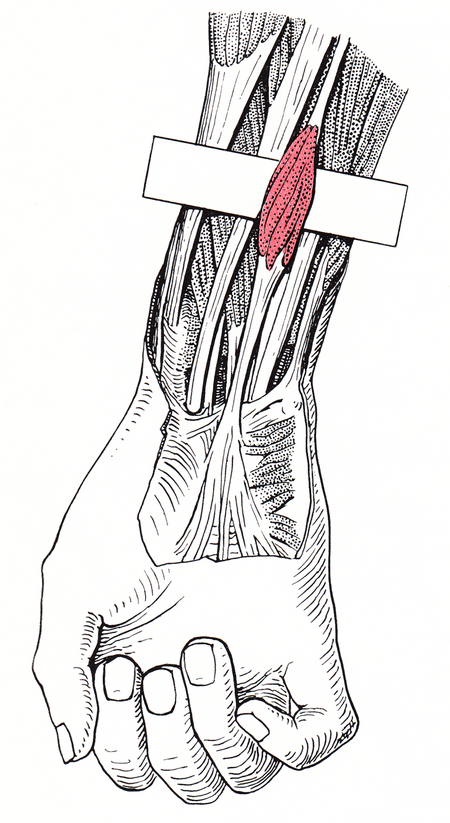
Muscle of the upper limb Palmaris longus musclePalmaris longus tendon as seen in surface anatomyDetailsOriginMedial epicondyle of humerus (common flexor tendon)InsertionPalmar aponeurosis and flexor retinaculum of the handArteryUlnar arteryNerveMedian nerveActionsWrist flexorAntagonistExtensor carpi radialis brevis, extensor carpi radialis longus, extensor carpi ulnarisIdentifiersLatinmusculus palmaris longusGreekΜακρύς παλαμικός μυςTA98A04.6.02.029TA22482FMA38462Anatomical ...

German economist Jens WeidmannChair of the Bank for International SettlementsIn officeNovember 2015 – 1 January 2022General ManagerJaime CaruanaAgustín CarstensPreceded byChristian NoyerSucceeded byFrançois Villeroy de GalhauPresident of the BundesbankIn office1 May 2011 – 31 December 2021Appointed byChristian WulffPreceded byAxel A. WeberSucceeded byJoachim Nagel Personal detailsBorn (1968-04-20) 20 April 1968 (age 56)Solingen, West Germany (now Germany)Education...

21°29′2″N 39°11′16″E / 21.48389°N 39.18778°E / 21.48389; 39.18778 بيت نصيفبيت نصيفمعلومات عامةنوع المبنى بيتالمكان جدة، منطقة مكة المكرمةالبلد السعوديةمعلومات أخرىالإحداثيات 21°29′02″N 39°11′16″E / 21.4839°N 39.1878°E / 21.4839; 39.1878 تعديل - تعديل مصدري - تعديل ويكي بيانات بيت نصيف�...

الجولة السابعة من موسم 2022 لفورمولا 1 قالب:SHORTDESC:الجولة السابعة من موسم 2022 لفورمولا 1 جائزة موناكو الكبرى 2022 جائزة فورمولا 1 موناكو الكبرى 2022 السباق 7 من أصل 23 السلسلة بطولة العالم لسباقات فورمولا 1 موسم 2022 البلد موناكو التاريخ بداية:27 مايو 2022 نهاية:29 مايو 2022 مكان ا...
