Read other articles:

Jembatan SeohaeKoordinat36°56′N 126°49′E / 36.94°N 126.82°E / 36.94; 126.82Moda transportasi6 lajur jalan tolLokalProvinsi Gyeonggi dan Provinsi Chungcheong SelatanRepublik KoreaNama resmiSeohae Grand BridgeKarakteristikDesainjembatan kabel pancangPanjang total7310 m[1]Lebar34 m[1]Bentang terpanjang470 m[1]SejarahPerancangSAMWOO[1]Mulai dibangun1993[1]Selesai dibangun2000[1]Dibuka9 November 2000[1]Lokasi J...

American physician Undated portrait John Strother Griffin (1816–1898) was a surgeon attached to the General Stephen W. Kearney expedition from New Mexico to California, a landowner and founder of East Los Angeles and a member of the Common Council of the city of Los Angeles, where he was one of the first university-trained physicians to settle. Family John Strother Griffin was born in Fincastle, Virginia, on June 25, 1816, to John Caswell Griffin and Mary Talbot Hancock, both of Virginia. H...

Peta pembagian administratif tingkat pertama dan kedua Gabon Pembagian administratif Gabon terdiri atas 9 provinsi pada tingkat pertama dan 50 departemen pada tingkat kedua. Tingkat ketiga pembagian administratif Gabon terdiri atas 152 kanton, 52 komune, 29 arondisemen, and 26 distrik. lbsPembagian administratif AfrikaNegaraberdaulat Afrika Selatan Afrika Tengah Aljazair Angola Benin Botswana Burkina Faso Burundi Chad Eritrea Eswatini Etiopia Gabon Gambia Ghana Guinea Guinea Khatulistiwa Guin...

English singer, presenter and actor (born 1962) For other people named Michael Ball, see Michael Ball (disambiguation). Michael BallOBEBall in 2006BornMichael Ashley Ball (1962-06-27) 27 June 1962 (age 61)Bromsgrove, Worcestershire, EnglandAlma materGuildford School of ActingOccupationsSingeractorpresenterYears active1984–presentKnown forLes MisérablesAspects of LoveHairsprayPartner(s)Cathy McGowan (1992–present)Musical careerGenresPopsoft rockmusical theatreeasy list...

First Love AgainPoster promosi untuk First Love AgainGenreKeluargaMelodramaDitulis olehPark Pil-jooSutradaraYoon Chang-beomPemeranMyung Se-binKim Seung-sooWang Bit-naPark Jung-chulNegara asal Korea SelatanBahasa asliKoreaJmlh. episode104ProduksiProduser eksekutifKim Sung-geunProduserKang Soo-yeonSong Min-yeobLokasi produksiKorea SelatanDurasi35 menitDistributorKBSRilis asliJaringanKBS2Format gambar1080i (HDTV)Format audioDolby DigitalRilis28 November 2016 (2016-11-28) –21 April 2...

European Union educational project This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Comenius programme – news · newspapers · books · scholar · JSTOR (December 2011) (Learn how and when to remove this template message) The Comenius programme is a European Union educational project. It concerns school-level education, and is part of the EU's Erasmus + 2014...

Wallachian (later Romanian) politician Constantin P. Olănescu (1845–May 14, 1928) was a Wallachian, later Romanian politician. Descended from an old Oltenian boyar family,[1] his father Pană was also in politics.[2] He was born in Bucharest and studied at the École Centrale des Arts et Manufactures in Paris. Upon his return home, Olănescu was successively named head of public works for Craiova (1869), department head at the Agriculture, Commerce and Public Works Mini...

Mason County, Kentucky, slave pen now at the National Underground Railroad Freedom Center in Cincinnati, Ohio The history of slavery in Kentucky dates from the earliest permanent European settlements in the state, until the end of the Civil War. In 1830, enslaved African Americans represented 24 percent of Kentucky's population, a share that had declined to 19.5 percent by 1860, on the eve of the Civil War. Most enslaved people were concentrated in the cities of Louisville and Lexington and ...

Helicopter system designed to be worn on a person's back The Pentecost HX-1 Hoppi-Copter, a functional backpack helicopter A backpack helicopter is a helicopter motor and rotor and controls assembly that can be strapped to a person's back, so they can walk about on the ground wearing it, and can use it to fly. It uses a harness like a parachute harness and should have a strap between the legs (so the pilot does not fall out of the harness during flight). Some designs may use a ducted fan desi...

Mithapukur Mosqueমিঠাপুকুর মসজিদReligionAffiliationIslamDistrictRangpurLocationMunicipalityMithapukurCountryBangladeshArchitectureTypemosqueThis article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Mithapukur Mosque – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and...

Pour les articles homonymes, voir Goa (homonymie). Goa गोंय Localisation de l'État en Inde. Administration Pays Inde Capitale Panaji Création 30 mai 1987 Langue officielle Konkani Gouverneur P. S. Sreedharan Pillai (en) Ministre en chef Pramod Sawant (en) (BJP) Démographie Population 1 458 545 hab. (2011[1]) Densité 394 hab./km2 Rang 27e Géographie Superficie 3 702 km2 Rang 28e modifier  Goa (गोंय (gõy)) est un État de la c�...

2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl（英文）（波兰文）2020年夏季奥林匹克运动会（東京）2021年7月23日至8月8日（受2019冠状病毒病疫情影响推迟，但仍保留原定名称）運動員206參賽項目24个大项旗手开幕式：帕维尔·科热尼奥夫斯基（游泳）和马娅·沃什乔夫斯卡（自行车）[1]闭幕式：卡罗利娜·纳亚（皮划艇）&#...

1995 American romantic drama film directed by Clint Eastwood This article is about the film. For the book, see The Bridges of Madison County. For the musical, see The Bridges of Madison County (musical). For the bridges, see List of Madison County Covered Bridges. The Bridges of Madison CountyTheatrical release poster by Bill GoldDirected byClint EastwoodScreenplay byRichard LaGraveneseBased onThe Bridges of Madison Countyby Robert James WallerProduced by Clint Eastwood Kathleen Kennedy Starr...

Day marking the anniversary of the end of Japanese rule over Taiwan on 25 October 1945 Retrocession DayObserved by Republic of ChinaTypeHistorical, cultural, nationalistDate25 October 1945Frequencyannual Retrocession DayTraditional Chinese臺灣光復節Simplified Chinese台湾光复节TranscriptionsStandard MandarinHanyu PinyinTáiwān guāngfùjiéHakkaRomanizationThòi-vân kông fu̍k chietSouthern MinTâi-lôTâi-uân kong-ho̍k tseh Retrocession Day is the name given...

Selección de fútbol de los Emiratos Árabes Unidos Datos generalesPaís Emiratos Árabes UnidosCódigo FIFA UAEFederación Federación de Fútbol de los Emiratos Árabes UnidosConfederación AFCSeleccionador  Paulo Bento (desde 2023-)Capitán Walid Abbas Más goles Ali Mabkhout (85)Más partidos Adnan Al Talyani (161)Clasificación FIFA 67.º (abril de 2024)Equipaciones Primera Segunda Primer partido Emiratos Árabes Unidos 1-0 CatarRiad, Arabia Saudita — 17 de marzo de 1972Copa de N...

Monumental gateway tower to Hindu temple complexes A gopuram or gopura (Tamil: கோபுரம், Telugu: గోపురం, Kannada: ಗೋಪುರ) is a monumental entrance tower, usually ornate, at the entrance of a Hindu temple, in the South Indian architecture of the southern Indian states of Tamil Nadu, Andhra Pradesh, Kerala, Karnataka, and Telangana,[1] and Sri Lanka. In other areas of India they are much more modest, while in Southern Indian temples they are very often ...

Regional news and information website Boston.comType of siteNewsAvailable inEnglishOwnerBoston Globe Media PartnersCreated byThe Boston GlobeEditorKaitlyn JohnstonGeneral managerMatthew KarolianURLboston.comCommercialYesLaunchedOctober 30, 1995; 28 years ago (1995-10-30)[1] Boston.com is a regional website that offers news and information about the Boston, Massachusetts, region.[2] It is owned and operated by Boston Globe Media Partners, publisher o...

この記事には参考文献や外部リンクの一覧が含まれていますが、脚注によって参照されておらず、情報源が不明瞭です。 脚注を導入して、記事の信頼性向上にご協力ください。（2020年2月） DIAC種類 受動素子ピン配置 アノード 1, アノード 2電気用図記号 テンプレートを表示 3層DIAC DIAC（ダイアック）は、ダイオードの一種。diode for alternating current（交流電流のためのダ�...

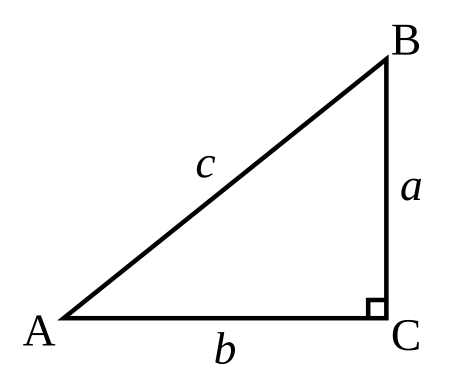
Polynomial equation whose integer solutions are sought Finding all right triangles with integer side-lengths is equivalent to solving the Diophantine equation a 2 + b 2 = c 2 . {\displaystyle a^{2}+b^{2}=c^{2}.} In mathematics, a Diophantine equation is an equation, typically a polynomial equation in two or more unknowns with integer coefficients, for which only integer solutions are of interest. A linear Diophantine equation equates to a constant the sum of two or more monomials, each of deg...

كعكة إسفنجيةمعلومات عامةالمنشأ إيطاليا بلد المطبخ ترتة الأمير رجنت — إكليل فرانكفورت — كعكة الأوبرا — تُرتة دُبُش النوع كعكة الرغوة المكونات الرئيسية طحين تعديل - تعديل مصدري - تعديل ويكي بيانات الكعكة الإسفنجية (بالإنجليزية: Sponge cake)‏ هي كعكة أو كيكة اسفنجية مكونة أساسا ...