Минимальная поверхность Шварца
|
Read other articles:

Cari artikel bahasa Cari berdasarkan kode ISO 639 (Uji coba) Kolom pencarian ini hanya didukung oleh beberapa antarmuka Halaman bahasa acak Bahasa EteosiprusDituturkan diPernah dituturkan di SiprusWilayahLaut Mediterania TimurEraAbad ke-10 hingga ke-4 SM[1] Rumpun bahasaBelum digolongkan Bahasa Eteosiprus Sistem penulisanAksara SiprusAspek ketatabahasaanTipologiBahasa isolat [sunting di Wikidata]Kode bahasaISO 639-3ecyLINGUIST ListecyGlottologeteo1240[2&#...

陆军第十四集团军炮兵旅陆军旗存在時期1950年 - 2017年國家或地區 中国效忠於 中国 中国共产党部門 中国人民解放军陆军種類炮兵功能火力支援規模约90门火炮直屬南部战区陆军參與戰役1979年中越战争 中越边境冲突 老山战役 成都军区对越轮战 紀念日10月25日 陆军第十四集团军炮兵旅(英語:Artillery Brigade, 14th Army),是曾经中国人民解放军陆军第十四集团军下属�...

City in the United States This article is about the city in Oregon. For the nearby geological formation, see Celilo Falls. For other uses, see Dalles. Not to be confused with the city of Dallas, Oregon. City in Wasco CountyThe DallesCityCity of the DallesThe Dalles and the Columbia River in November 2008 FlagSealMotto(s): Cognito timor Vincit (Latin), Knowledge Conquers Fear (English)Location in OregonCoordinates: 45°36′06″N 121°10′30″W / 45.60167°N 121.17500°...

Artikel ini bukan mengenai Trans Metro Deli. Trans MebidangTrans MebidangInfoPemilikDinas Perhubungan Provinsi Sumatra UtaraWilayahKota Medan, Kota Binjai, dan Kabupaten Deli SerdangJenisbus raya terpaduJumlah jalur2OperasiDimulaiAkhir tahun 2015OperatorDAMRI Halte bus Trans Mebidang di depan Medan Mall, Pusat Pasar, Medan Kota, Medan. Trans Mebidang adalah sebuah bus raya terpadu di Sumatera Utara yang beroperasi di dareah Mebidang (Kota Medan, Kota Binjai, dan Kabupaten Deli Serdang). Diope...

Artikel ini hampir seluruhnya merupakan ringkasan alur. Artikel ini harus diperluas untuk menyediakan cakupan konteks dunia nyata yang lebih seimbang. Please edit the article to focus on discussing the work rather than merely reiterating the plot. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Pocong Minta Kawinposter filmSutradaraHarry Dagoe SuharyadiChiska DoppertProduserHarry Dagoe SuharyadiDitulis olehArmantono, Chiska Doppert, Harry Dagoe SuharyadiPemeranJulia PerezV...
У этого термина существуют и другие значения, см. Красная книга (значения). Красная книга Российской Федерации (ККРФ) — основной государственный документ, учреждённый в целях выявления редких и находящихся под угрозой исчезновения диких животных, дикорастущих растен�...

Partial suppression of a law This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (May 2023) Derogation is a legal term of art,[1][2] which allows for part or all of a provision in a legal measure to be applied differently, or not at all, in certain cases.[3] The term is also used in Catholic canon law,[4] and in this con...

Voce principale: Molde Fotballklubb. Molde F.K.Stagione 2019Sport calcio Squadra Molde Allenatore Erling Moe Assistente Trond Strande Eliteserien1º posto (in Champions League) Coppa di NorvegiaTerzo turno Europa LeagueSpareggi Maggiori presenzeCampionato: Aursnes (30)Totale: Aursnes (39) Miglior marcatoreCampionato: James (17)Totale: James (24) 2018 2020 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti il Molde Fotballklubb nelle competizioni uff...

Municipal unit in Elbasan, AlbaniaGjergjanMunicipal unitGjergjanCoordinates: 41°3′N 20°2′E / 41.050°N 20.033°E / 41.050; 20.033Country AlbaniaCountyElbasanMunicipalityElbasanPopulation (2011) • Municipal unit5,126Time zoneUTC+1 (CET) • Summer (DST)UTC+2 (CEST) Gjergjan is a village and a former municipality in the Elbasan County, central Albania. At the 2015 local government reform it became a subdivision of the municipality El...
Penikese IslandPenikese Island from the southeast in 2005.Penikese IslandShow map of MassachusettsPenikese IslandShow map of the United StatesGeographyCoordinates41°27′00″N 70°55′23″W / 41.4501071°N 70.9230909°W / 41.4501071; -70.9230909[1]ArchipelagoElizabeth IslandsTotal islands1Area.117 sq mi (0.30 km2)Highest elevation52 ft (15.8 m)AdministrationUnited StatesStateMassachusettsCountyDukes County The Elizabeth Islands...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Taufik Batisah – ...
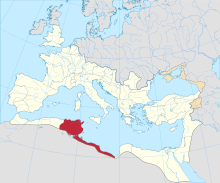
Ancient Roman–Berber city in late antiquity Africa Proconsularis (125 AD) Octaba was an ancient Roman–Berber city in the province of Africa Proconsularis and Byzacena in late antiquity. Its exact location is now lost, but it was in the Sahel region of Tunisia. In antiquity, Octaba was the seat of an ancient bishopric which survived till the 7th century. The only known bishop of this diocese is Albinus, who took part in the synod gathered in Carthage by the Vandal king of Huneric in 48...

Not to be confused with Italy-based international Catholic radio broadcasting service Radio Maria. Polish radio station Radio MaryjaCompany typeSubsidiaryIndustryRadio broadcastingFoundedDecember 8, 1991; 32 years ago (1991-12-08)HeadquartersToruń, PolandKey peopleTadeusz Rydzyk – Founder and Director;Jan Król – Vice-directorParentLux Veritatis FoundationWebsiteradiomaryja.pl Radio Maryja [ˈradjɔ maˈrɨja] is a religious and political socially conservative ...

Pub in Bankside, London The Anchor The Anchor is a pub in the London Borough of Southwark. It is in the Bankside locality on the south bank of the River Thames, close to Southwark Cathedral and London Bridge station. A tavern establishment (under various names) has been at the pub's location for over 800 years.[1] Behind the pub are buildings that were operated by the Anchor Brewery.[1] The Anchor started life as the brewery tap room for the Anchor Brewery, first established i...

Uno scavo archeologico La tomba di Tutankhamon appena scoperta L'archeologia (dal greco ἀρχαιολογία, composto dalle parole ἀρχαῖος, antico, e λόγος, discorso o studio) è la scienza che studia le civiltà e le culture umane del passato e le loro relazioni con l'ambiente circostante, mediante la raccolta, la documentazione e l'analisi delle tracce materiali che hanno lasciato popoli antichi (architetture, manufatti, resti biologici e umani). Indice 1 Storia 1.1 Premes...

Domenico Scarlatti ritratto da Domingo Antonio Velasco (1738) Giuseppe Domenico Scarlatti (Napoli, 26 ottobre 1685 – Madrid, 23 luglio 1757) è stato un clavicembalista e compositore italiano, attivo durante l'età barocca. Cronologicamente, è classificato come un compositore barocco, anche se la sua musica è stata di riferimento nello sviluppo dello stile classico, e conosciuta ed ammirata dai musicisti successivi, romantici compresi. La sua produzione più nota, realizzata dopo il suo t...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Wat Ko, Bangkok – news · newspapers · books · scholar · JSTOR (March 2021) (Learn how and when to remove this message) Wat Ko in 2023 This article is about Wat Ko in Taling Chan. For Wat Ko in Samphanthawong or Chinatown, see Wat Samphanthawongsaram. Buddhist t...

Local election held in Malta in 2008 Politics of Malta Republic Constitution President (list) George Vella Government Prime Minister (list) Robert Abela Deputy Prime Minister (list) Chris Fearne Cabinet (current) Parliament Speaker (list) Angelo Farrugia Deputy Speaker (list) David Agius Leader of the House (list) Owen Bonnici Leader of the Opposition (list) Bernard Grech Judiciary Chief Justice (list) Mark Chetcuti Law Courts and Tribunals Commission for theAdministration of Justice Politica...

English sailor and privateer (c. 1540 – 1596) This article is about the Elizabethan naval commander. For other uses, see Francis Drake (disambiguation). Vice admiralSir Francis DrakePortrait by Marcus Gheeraerts, 1591Bornc. 1540Tavistock, Devon, EnglandDied28 January 1596 (1596-01-29) (aged 56)Portobelo, Colón, PanamaSpouses Mary Newman (m. 1569; died 1581) Elizabeth Sydenham (m. 1585)AwardsKnight ...

2D surface which extends indefinitely For other uses, see Plane (disambiguation). In mathematics, a plane is a two-dimensional space or flat surface that extends indefinitely. A plane is the two-dimensional analogue of a point (zero dimensions), a line (one dimension) and three-dimensional space. When working exclusively in two-dimensional Euclidean space, the definite article is used, so the Euclidean plane refers to the whole space. Several notions of a plane may be defined. The Euclidean p...






