–€–Α–Κ―¹–Η–Φ–Α–Μ―¨–Ϋ―΄–Ι ―Ä–Α–Ζ―Ä–Β–Ζ –≥―Ä–Α―³–Α
|
Read other articles:

Cet article concerne l'auteur de bandes dessinΟ©es franΟßais. Pour le personnage de la sΟ©rie de bandes dessinΟ©es Les Tuniques bleues, voir Caporal Blutch. Pour les articles homonymes, voir Hincker. BlutchBlutch en 2021.Naissance 27 dΟ©cembre 1967 (56 ans)StrasbourgNom de naissance Christian HinckerNationalitΟ© franΟßaiseActivitΟ©s Auteur de bande dessinΟ©e, dessinateur de bande dessinΟ©e, scΟ©nariste de bande dessinΟ©e, illustrateurFormation Οâcole supΟ©rieure des arts dΟ©coratifs...

Ό³ΌÖΊΙΊßΌÜΌç ΊΘΊ°Ί±ΌâΊ¨ ΊΖΊßΌ³ΊΙ Ί±ΊßΌ¹ΌäΌÜΊß (ΊΣΌàΊΕΌäΊ≠). Ί±ΊßΌ¹ΌäΌÜΊß ΊßΌ³ΊΞΊ≠Ί·ΊßΊΪΌäΊßΊΣ 42¬Α28βÄ≤35βÄ≥N 73¬Α48βÄ≤51βÄ≥W / 42.476388888889¬ΑN 73.814166666667¬ΑW / 42.476388888889; -73.814166666667 [1] ΊΣΊßΊ±ΌäΊ° ΊßΌ³ΊΣΊΘΊ≥ΌäΊ≥ 1914 ΊΣΌ²Ί≥ΌäΌÖ ΊΞΊ·ΊßΊ±Όä ΊßΌ³Ί®Ό³Ί· ΊßΌ³ΌàΌ³ΊßΌäΊßΊΣ ΊßΌ³ΌÖΊΣΊ≠Ί·Ί©[2] ΊßΌ³ΊΣΌ²Ί≥ΌäΌÖ ΊßΌ³ΊΘΊΙΌ³Όâ ΌÖΌ²ΊßΊΖΊΙΊ© ΊΘΌ³Ί®ΊßΌÜΌä Ί°ΊΒΊßΊΠΊΒ Ί§ΊΚΊ±ΊßΌ¹ΌäΊ© ΊßΌ³ΌÖΊ≥ΊßΊ≠Ί© 3...

Municipality in Lower Saxony, GermanyJameln MunicipalityLocation of Jameln within LΟΦchow-Dannenberg district Jameln Show map of GermanyJameln Show map of Lower SaxonyCoordinates: 53¬Α02βÄ≤32βÄ≥N 11¬Α04βÄ≤43βÄ≥E / 53.04222¬ΑN 11.07861¬ΑE / 53.04222; 11.07861CountryGermanyStateLower SaxonyDistrictLΟΦchow-Dannenberg Municipal assoc.ElbtalaueSubdivisions10 OrtsteileGovernment βÄΔ MayorUdo SperlingArea βÄΔ Total35.84 km2 (13.84 sq mi)Elev...

Penghargaan Dadasaheb PhalkeJenisNasionalKategoriSinema IndiaDeskripsiPenghargaan Prestasi Seumur HidupDiinstitusikan1969Penghargaan pertama1969Penghargaan terakhir2015Total yang diberi penghargaan46Dianugerahi olehDirektorat Festival FilmBiaya penghargaanβ²Ι1.000.000 (US$14,000)MedaliSwarna Kamal (Teratai Emas)Penerima pertamaDevika RaniPenerima saat iniManoj Kumar Penghargaan Dadasaheb Phalke adalah penghargaan tertinggi dalam bidang sinema di India. Penghargaan tersebut dipe...

Artikel ini berisi konten yang ditulis dengan gaya sebuah iklan. Bantulah memperbaiki artikel ini dengan menghapus konten yang dianggap sebagai spam dan pranala luar yang tidak sesuai, dan tambahkan konten ensiklopedis yang ditulis dari sudut pandang netral dan sesuai dengan kebijakan Wikipedia. (Januari 2022) Putera Sampoerna FoundationTanggal pendirian2001; 23 tahun lalu (2001)PendiriPutera SampoernaTipeYayasanLokasiJakarta, IndonesiaPemilikKeluarga besar Putera SampoernaDewan PembinaK...

A computer text file character representing blank space Dot space redirects here. For the animated film, see Dot in Space. βêΘ redirects here. Not to be confused with βçΫ or ⨥. A whitespace character is a character data element that represents white space when text is rendered for display by a computer. For example, a space character (U+0020 SPACE, ASCII 32) represents blank space such as a word divider in a Western script. A printable character results in output when rendered, ...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

ψ¹™ψ¹°η®‰δΚ΄ψ¹·φΛ€η®Φεè·ηÉΫψ¹Σεè²ηÄÉφ•΅γ¨°ψ²³ε΅ΚεÖΗψ¹¨εÖ®ψ¹èγΛΚψ¹ïψ²¨ψ¹Πψ¹³ψ¹Σψ¹³ψ¹΄ψĹδΗçεç¹εàÜψ¹ßψ¹ôψIJε΅ΚεÖΗψ²£ηΩΫεä†ψ¹½ψ¹Π箉δΚ΄ψ¹°δΩΓι†ΦφÄßεêëδΗäψ¹Ϊψ¹îεçîεä¦ψ¹èψ¹†ψ¹ïψ¹³ψIJοΦàψ¹™ψ¹°ψÉÜψÉ≥ψɽψɧψÉΦψÉàψ¹°δΫΩψ¹³φ•ΙοΦâε΅ΚεÖΗφΛ€γ¥Δ?: ψ²≥ψÉΪψ²· βÄ™ ψÉ΄ψÉΞψÉΦψ²Ι ¬Ζ φ¦Ηγ±ç ¬Ζ ψ²Ιψ²ΪψÉ©ψÉΦ ¬Ζ CiNii ¬Ζ J-STAGE ¬Ζ NDL ¬Ζ dlib.jp ¬Ζ ψ²ΗψÉΘψÉëψÉ≥ψ²ΒψÉΦψɹ ¬Ζ TWLοΦà2017εΙ¥4φ€àοΦâ ψ²≥ψÉΪψ²·ψ²£φâ™ψ¹Γφä€ψ¹³ψ¹ΠδΫ€ψ¹Θψ¹üγ™Εψ¹°φ†™ ψ²≥ψÉΪψ²·οΦàφ€®φ†™ψĹοΩΫ...

American professional soccer club Soccer clubCharlotte EaglesFull nameCharlotte Eagles Soccer ClubNickname(s)The EaglesFounded1991; 33 years ago (1991)StadiumSportsplex at MatthewsMatthews, North CarolinaCapacity2,300PresidentDavid UrbanHead CoachMichael KovachLeagueUSL League Two20232nd, South Atlantic DivisionPlayoffs: Conference QuarterfinalsWebsiteClub website Home colors Away colors The Charlotte Eagles is an American professional soccer team based in Charlotte, North C...

ΌÜΌ΅Ί®ΌÜΊ·ΊßΌÜ ΌÜΌ΅Ί®ΌÜΊ·ΊßΌÜ city ΊßΌ³ΊßΊ≥ΌÖ ΊßΌ³Ί±Ί≥ΌÖΌä Nehbandan ΊßΌ³ΊΞΊ≠Ί·ΊßΊΪΌäΊßΊΣ 31¬Α32βÄ≤31βÄ≥N 60¬Α02βÄ≤11βÄ≥E / 31.54194¬ΑN 60.03639¬ΑE / 31.54194; 60.03639 ΊΣΌ²Ί≥ΌäΌÖ ΊΞΊ·ΊßΊ±Όä ΊßΌ³Ί·ΌàΌ³Ί© ΊΞΌäΊ±ΊßΌÜ ΊßΌ³ΌÖΊ≠ΊßΌ¹ΊΗΊ© Ί°Ί±ΊßΊ≥ΊßΌÜ Ί§ΌÜΌàΊ®Όä ΊßΌ³ΌÖΌ²ΊßΊΖΊΙΊ© ΌÖΌ²ΊßΊΖΊΙΊ© ΌÜΌ΅Ί®ΌÜΊ·ΊßΌÜ ΊßΌ³ΌÜΊßΊ≠ΌäΊ© Central ΊΙΊßΊΒΌÖΊ© Ό³ΌÄ ΌÖΌ²ΊßΊΖΊΙΊ© ΌÜΌ΅Ί®ΌÜΊ·ΊßΌÜ Ί°ΊΒΊßΊΠΊΒ Ί§ΊΚΊ±ΊßΌ¹ΌäΊ© ΊßΊ±ΊΣΌ¹ΊßΊΙ 1187 ΌÖΊΣΊ±[1]...

Gambar lap. Grand Prix F1 Jerman 2004 merupakan balapan Formula 1 pada 25 Juli 2004 di Hockenheimring.[1] Lomba Pos No Pembalap Tim Lap Waktu/Tersingkir Grid Poin 1 1 Michael Schumacher Ferrari 66 1:23'54.848 1 10 2 9 Jenson Button BAR-Honda 66 +8.388 detik 13 8 3 8 Fernando Alonso Renault 66 +16.351 detik 5 6 4 5 David Coulthard McLaren-Mercedes 66 +19.231 detik 4 5 5 3 Juan Pablo Montoya Williams-BMW 66 +23.055 detik 2 4 6 14 Mark Webber Jaguar-Cosworth 66 +41.108 detik 11 3 7 4 Ant...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Thomas Bartholomew Curran βÄ™ news ¬Ζ newspapers ¬Ζ books ¬Ζ scholar ¬Ζ JSTOR (August 2022) For other people named Thomas Curran, see Thomas Curran (disambiguation). Thomas Bartholomew Curran (1870 βÄ™ 1929) was an Irish barrister and an Anti-Parnellite/Iri...

Soldier; 25th Chief of Clan Maclean (1798βÄ™1883) Sir Charles Fitzroy Maclean25th Clan Chief9th Baronet of Morvern5th Lord MacleanIn office1847βÄ™1883Preceded bySir Fitzroy Jeffreys Grafton Maclean, 8th Baronet, fatherSucceeded bySir Fitzroy Donald Maclean, 10th Baronet, son Personal detailsBornFitzroy Donald Maclean(1798-10-14)14 October 1798Died27 January 1883(1883-01-27) (aged 84)Folkestone, Kent, EnglandSpouseEmily Eleanor MarshamChildrenSir Fitzroy Donald Maclean, 10th BaronetParent...

Exonym used to describe Indigenous people from the circumpolar region For other uses, see Eskimo (disambiguation). Ethnic group EskimoIllustration of a Greenlandic Inuit manTotal population183,500Regions with significant populationsRussia- Chukotka Autonomous Okrug- Sakha (Yakutia) United States- AlaskaCanada- Newfoundland and Labrador- Northwest Territories - Nunavut- Quebec- Yukon (formerly) GreenlandLanguagesEskaleut languages (Aleut, Greenlandic, Inuktut, Inuit languages, Yupik), Russian,...

1940 film by Anatole Litvak City for ConquestTheatrical release posterDirected byAnatole LitvakJean Negulesco (uncredited)Screenplay byJohn WexleyBased onCity for Conquest1936 novelby Aben KandelProduced byAnatole LitvakHal B. Wallis (uncredited)StarringJames CagneyAnn SheridanArthur KennedyFrank CravenAnthony QuinnElia KazanCinematographyJames Wong HoweSol PolitoEdited byWilliam HolmesMusic byMax SteinerDistributed byWarner Bros.Release date September 21, 1940 (1940-09-21) Run...
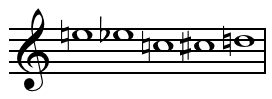
Set class redirects here. For the concept in set theory, see Class (set theory). Six-element set of rhythmic values used in Variazioni canoniche by Luigi Nono[1] A set (pitch set, pitch-class set, set class, set form, set genus, pitch collection) in music theory, as in mathematics and general parlance, is a collection of objects. In musical contexts the term is traditionally applied most often to collections of pitches or pitch-classes, but theorists have extended its use to other typ...

Illusions or tricks to change appearance Creature effects redirects here. For the company, see Creature Effects, Inc. For other uses, see Special Effects (disambiguation). This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (June 2017) (Learn how and when to remove this message) A special effect of a miniature person from the 1952 film The Seven Deadly Sins Specia...

Virginia Air National GuardAn F-22 Raptor of the 149th Fighter Squadron at Joint Base LangleyβÄ™Eustis. The 149th is the oldest unit in the Virginia Air National Guard, having over 70 years of service to the commonwealth and nation.Active21 June 1947 - presentCountry United StatesAllegiance VirginiaBranch Air National GuardTypemilitary reserve force, state militiaRoleTo meet commonwealth and federal mission responsibilities.Size1,200Part ofVirginia National GuardUnited S...

ψ¹™ψ¹°η®‰δΚ΄ψ¹·φΛ€η®Φεè·ηÉΫψ¹Σεè²ηÄÉφ•΅γ¨°ψ²³ε΅ΚεÖΗψ¹¨εÖ®ψ¹èγΛΚψ¹ïψ²¨ψ¹Πψ¹³ψ¹Σψ¹³ψ¹΄ψĹδΗçεç¹εàÜψ¹ßψ¹ôψIJ ε΅ΚεÖΗψ²£ηΩΫεä†ψ¹½ψ¹Π箉δΚ΄ψ¹°δΩΓι†ΦφÄßεêëδΗäψ¹Ϊψ¹îεçîεä¦ψ¹èψ¹†ψ¹ïψ¹³ψIJοΦàψ¹™ψ¹°ψÉÜψÉ≥ψɽψɧψÉΦψÉàψ¹°δΫΩψ¹³φ•ΙοΦâε΅ΚεÖΗφΛ€γ¥Δ?: ψ²Πψ²ΚψÉôψ²·δΚΚ βÄ™ ψÉ΄ψÉΞψÉΦψ²Ι ¬Ζ φ¦Ηγ±ç ¬Ζ ψ²Ιψ²ΪψÉ©ψÉΦ ¬Ζ CiNii ¬Ζ J-STAGE ¬Ζ NDL ¬Ζ dlib.jp ¬Ζ ψ²ΗψÉΘψÉëψÉ≥ψ²ΒψÉΦψɹ ¬Ζ TWL (2010εΙ¥9φ€à) ψ²Πψ²ΚψÉôψ²·Oβĉzbeklar–é–Ζ–±–Β–Κ–Μ–Α―Äψ²Πψ²ΚψÉôψ²·ψ¹°δΚΚψÄÖγΖèοΩΫ...

Lo stesso argomento in dettaglio: Campionato mondiale di Formula 1 1953. Gran Premio di Francia 1953 28¬Κ GP del Mondiale di Formula 1Gara 5 di 9 del Campionato 1953 Data 5 luglio 1953 Nome ufficiale XL Grand Prix de l'A.C.F. Luogo Circuito di Reims Percorso 8,347 km / 5,187 US mi Circuito stradale Distanza 60 giri, 500,820 km/ 311,195 US mi Clima Sereno Risultati Pole position Giro piΟΙ veloce Alberto Ascari Juan Manuel Fangio Ferrari in 2'412 Maserati in 2'410 (nel giro 25) Podio 1. ...






