Красная площадь (фильм)
| |||||||||||||||||||||||||||||
Read other articles:

العلاقات الإماراتية الوسط أفريقية الإمارات العربية المتحدة جمهورية أفريقيا الوسطى الإمارات العربية المتحدة جمهورية أفريقيا الوسطى تعديل مصدري - تعديل العلاقات الإماراتية الوسط أفريقية هي العلاقات الثنائية التي تجمع بين الإمارات العربية المتحدة وجمهو�...

YanusRaja Yanus dan Ratu Charlotte di Katedral ChartresRaja SiprusBerkuasa9 September 1398 - 29 Juni 1432PendahuluJacques IPenerusJean IIInformasi pribadiKelahiran1375GenovaKematian29 Juni 1432NikosiaWangsaWangsa LusignanAyahJacques I dari SiprusIbuHelvis dari Brunswick-GrubenhagenPasanganAnglesia ViscontiCharlotte de BourbonAnakJean II dari SiprusAnne dari Siprus Yanus dari Siprus (1375 – 29 Juni 1432) merupakan seorang Raja dari Siprus dan tituler Raja Armenia Kilikia dan Yerusalem dari t...
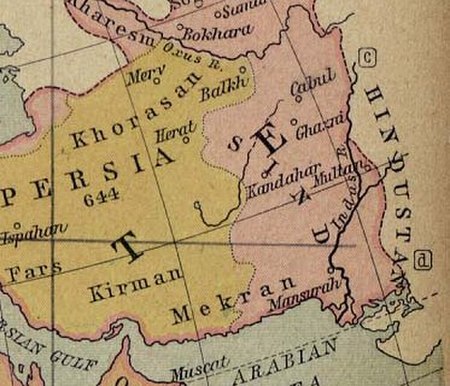
Historical region of Greater Iran This article is about the historical region comprising northeastern Iran, parts of Afghanistan and Central Asia. For the Iranian province of Khorasan, see Khorasan Province. For other uses, see Khorasan. RegionGreater Khorasan خراسان بزرگHistorical Khorasan or Ancient KhorasanRegionMap of Khorasan and its surroundings in the 7th/8th centuriesCountries in KhorasanAfghanistan, Iran and Turkmenistan.[1] Different regions of Tajikistan, Pakistan...

Israël au Concours Eurovision Pays Israël Radiodiffuseur KAN Émission de présélection Hakochav HaBa L'Eurovizion (artiste)HaShir Shelanu L'Eurovizion (chanson, depuis 2020) Participations 1re participation Eurovision 1973 Participations 46 (en 2024) Meilleure place 1er (en 1978, 1979, 1998 et 2018) Moins bonne place 24e en demi-finale (en 2007) Liens externes Page officielle du diffuseur Page sur Eurovision.tv Pour la participation la plus récente, voir :Israël au Concours ...

American politician For the line engraver, see James C. Allen (engraver). James Cameron AllenClerk of the United States House of RepresentativesIn office1857–1860Preceded byWilliam CullomSucceeded byJohn W. ForneyMember of the U.S. House of Representativesfrom Illinois's At-large districtIn officeMarch 4, 1863 – March 3, 1865Preceded byDistrict createdSucceeded bySamuel W. MoultonMember of the U.S. House of Representativesfrom Illinois's 7th districtIn off...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Spanish actress This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (January 2013) (Learn how and when to remove this message) In this Spanish name, the first or paternal surname is Jiménez and the second or maternal family name is Arranz. Lucía JiménezBornLucía Jiménez Arranz (1978-11-21) 21 November 1978 (age ...

Private university in Argentina Austral UniversityUniversidad AustralAustral University's Pilar CampusMottoStudiorum australis universitasTypePrivate universityEstablished1991Religious affiliationRoman CatholicRectorJulián RodríguezAcademic staff1200Undergraduates4000LocationBuenos Aires, Rosario, and Pilar, Argentina.34°27′24″S 58°51′32″W / 34.45667°S 58.8589°W / -34.45667; -58.8589CampusSuburbanWebsitehttp://www.austral.edu.ar Austral University (Spanis...

Russian footballer (born 1990) In this name that follows Eastern Slavic naming customs, the patronymic is Mikhaylovich and the family name is Smolov. Fyodor Smolov Smolov with Dynamo Moscow in 2022Personal informationFull name Fyodor Mikhailovich SmolovDate of birth (1990-02-09) 9 February 1990 (age 34)[1]Place of birth Saratov, Russian SFSR, Soviet UnionHeight 1.86 m (6 ft 1 in)[2]Position(s) StrikerTeam informationCurrent team KrasnodarYouth career199...

La Consegna delle chiaviAutoreGiambattista Pittoni Data1730-1735 Tecnicaolio su tela Dimensioni82×42 cm UbicazioneLouvre, Parigi Consegna delle chiavi, è un dipinto realizzato indicativamente nel 1730 dal pittore italiano Giambattista Pittoni.[1] Indice 1 Storia 2 Descrizione 3 Esposizioni 4 Argomenti correlati 5 Note 6 Bibliografia 7 Collegamenti esterni Storia L'episodio è tratto dal Vangelo (secondo San Matteo, 16: 18-20) Ci fu un primo bozzetto per una pala d'altare, della...

11gatsu no AnkletSingel oleh AKB48dari album Bokutachi wa, Ano Hi no Yoake wo ShitteiruBahasaJepangDirilis22 November 2017FormatCD Digital SingleGenreJ-PopDurasi4:26Label You, Be Cool! / King Genie Music Stone Music Entertainment ProduserYasushi AkimotoKronologi singel AKB48 Sukinanda (2017) 11gatsu no Anklet (2017) Jabaja (2018) Music video (Full ver.)11gatsu no Anklet di YouTube 11gatsu no Anklet (11月のアンクレット, November's Anklet) adalah singel ke-50 dari AKB48, yang dirilis pa...

Type of vegetarianism Ovo-vegetarians consume eggs, but not dairy or animal flesh. Comparison of selected vegetarian and semi-vegetarian diets (view template) Plants Dairy Eggs Seafood Poultry All other animals Vegetarianism Ovo-lacto vegetarianism Yes Yes Yes No No No Ovo vegetarianism Yes No Yes No No No Lacto vegetarianism Yes Yes No No No No Veganism Yes No No No No No Semi-vegetarianism Flexitarianism Yes Yes Yes Sometimes Sometimes Sometimes Pollotarianism Yes Maybe Maybe Maybe Yes No P...

伊斯蘭教,是澳門地區的少數宗教。目前,澳門有大約400多名穆斯林,他們稱自己為澳門伊斯蘭社團。[1]但根據香港伊斯蘭協會,包括所有外國穆斯林工人(如孟加拉國,印度,印度尼西亞和巴基斯坦),澳門的穆斯林人數超過1萬人。[2] 歷史 元代 自元朝至清,伊斯蘭教一直存在於澳門。人們普遍認為伊斯蘭教是由中東和波斯的商人帶到澳門的。[3]其中一�...

後ウマイヤ朝 الخلافة الأموية في الأندلس (アラビア語) ← ← 756年 - 1031年 → 後ウマイヤ朝の領域 公用語 アラビア語 首都 コルドバ アミール 756年 - 788年 アブド・アッラフマーン1世 カリフ 1027年 - 1031年ヒシャーム3世(英語版) 変遷 建国 756年 アブド・アッラフマーン3世がカリフに即位929年 滅亡1031年 後ウマイヤ朝(こうウマイヤちょう、756年 - 1031年)�...

Cet article est une ébauche concernant l’Irlande, l’Union européenne et une élection ou un référendum. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. 1979 1989 Élections européennes de 1984 en Irlande 15 députés européens 14 juin 1984 Corps électoral et résultats Inscrits 2 413 404 Votants 1 147 745 47,6 % 16 Votes exprimés 1 120 416 Blancs et n...

Alois AlzheimerAlois AlzheimerLahirAloysius Alzheimer(1864-06-14)14 Juni 1864Marktbreit, Kerajaan Bayern, Konfederasi JermanMeninggal19 Desember 1915(1915-12-19) (umur 51)Breslau, Provinsi Schlesien, Kerajaan PrusiaPendidikan Universitas Eberhard Karl Tübingen Universitas Julius Maximilian Würzburg Universitas Friedrich Wilhelm Dikenal atasPenemu penyakit demensia prapikun (Penyakit Alzheimer)ProfesiDokter, psikiaterInstitusi Institut Gangguan Jiwa dan Epilepsi (Irrenschloss) Frankfur...

Туркмены на Украине (туркм. Ukrainadaky türkmenler, укр. Туркмени в Україні) — туркменское национальное меньшинство, проживающее на Украине и составляющее часть туркменской диаспоры. Родным языком туркмен является туркменский, который принадлежит к тюркской языковой семье, по ве�...

The Village Voice Formato tabloidePaís Estados UnidosSede Nueva YorkFundación 1955Fin de publicación 21 de septiembre de 2017 (edición impresa)Idioma inglésPropietario(a) Carter BurdenISSN 0042-6180Sitio web http://www.villagevoice.com/[editar datos en Wikidata] The Village Voice es un periódico de noticias y cultura de Estados Unidos, conocido por ser el primer periódico semanal alternativo del país. Fundado en 1955 por Ed Fancher, Dan Wolf, John Wilcock, y Norman Mailer, l...
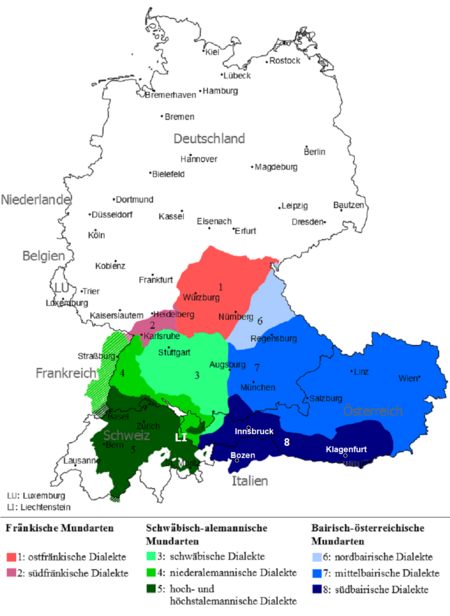
Upper German dialect This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: South Franconian German – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) South FranconianNative toGermany (Baden-Württemberg)Language familyIndo-European GermanicWest GermanicEl...

Continuous maps on a closed subset of a normal space can be extended Pavel Urysohn In topology, the Tietze extension theorem (also known as the Tietze–Urysohn–Brouwer extension theorem or Urysohn-Brouwer lemma[1]) states that any real-valued, continuous function on a closed subset of a normal topological space can be extended to the entire space, preserving boundedness if necessary. Formal statement If X {\displaystyle X} is a normal space and f : A → R {\displaystyle f:A\t...
