Ивков, Борислав

В Википедии есть статьи о других людях с фамилией Ивков.
Шахматы
Борислав Ивков
серб. Борислав Ивков
1972 год
1972 год
Страны  Югославия
Дата рождения 12 ноября 1933(1933-11-12)
Место рождения
Дата смерти 14 февраля 2022(2022-02-14)[1][2] (88 лет)
Место смерти
Звание гроссмейстер (1955)
международный мастер (1954)
Максимальный рейтинг 2570 (июнь 1967)
Актуальный рейтинг 2402 (январь 2022)
Логотип Викисклада Медиафайлы на Викискладе

Бо́рислав И́вков (серб. Борислав Ивков; 12 ноября 1933, Белград — 14 февраля 2022[1][2], Белград[3]) — сербский, ранее югославский, шахматист, гроссмейстер (1955), тренер, первый в истории шахмат чемпион мира среди юношей (1951). Член символического клуба победителей чемпионов мира Михаила Чигорина с 30 ноября 1968 года. Международный арбитр (1986).

Спортивные результаты

Год Турнир + − = Результат Место
1948 Чемпионат Югославии среди юношей 1-2
1949 Загреб, 5-й чемпионат Югославии 6 3 10 11 из 19 4-7
1950 Блед 5 4 5 7½ из 14 5-6
1951 Сараево, 7-й чемпионат Югославии 4 4 11 9½ из 19 10-12
1952 Белград, чемпионат Югославии 4 3 12 10 из 19 7-9
1953 Опатия 5 2 10 10 из 17 4-6
Копенгаген
1954 Белград 6 2 11 11½ из 19 4-5
1955 Буэнос-Айрес 10 1 6 13 из 17 1
Мар-дель-Плата 9 1 5 11½ из 15 1
Загреб 7 1 11 12½ из 19 2-3
Нови-Сад 7 3 7 10½ из 17 3-4
1955/56 Гастингс 5 1 3 6½ из 9 3
1956 Москва, 12-я олимпиада (на 2-й, 3-й досках) 9 1 6 12 из 16
1958 Сараево, 13-й чемпионат Югославии 6 0 13 12½ из 19 1-2
Мюнхен, 13-я олимпиада (на 1-й, 2-й, 3-й досках) 7 3 5 9½ из 15
Богнор-Риджис 1-3
1959 Сараево 1-2
Сантьяго 1
Лима 1
Мар-дель-Плата 3-4
Дрезден 3-4
1960 Лейпциг, 14-я олимпиада (на 2-й, 3-й досках) 9 1 6 12 из 16
1961 Бевервейк 1-2
1962 Варна, 15-я олимпиада (на 2-й, 3-й, 4-й досках) 11 0 5 13½ из 16
Нови-Сад 1
1963 Зеница, 19-й чемпионат Югославии 10 1 10 15½ из 21 1-2
Сараево 2-5
Бевервейк 3-5
1964 Амстердам, межзональный турнир 9 2 12 15 из 23 7
Тель-Авив, 16-я олимпиада (на 1-й, 2-й досках) 8 1 7 11½ из 16
Сараево 3
Бевервейк 4
Белград 2-3
1965 Загреб 1-2
Гавана 2-4
1966 Гавана, 17-я олимпиада (на 1-й, 2-й досках) 8 3 4 10 из 15
Сараево 3-4
Бевервейк 4
Венеция 1
1967 Сус, межзональный турнир 6 5 10 11 из 21 11-12
Сараево 1-2
1968 Лугано, 18-я олимпиада (на 1-й, 2-й досках) 5 1 8 9 из 14
Сомбор 1-3
Малага 1-2
1969 Малага 1-2
Белград 1-4
Поляница-Здруй 4
1970 СССР — сборная мира (на 10-й доске ) 0 2 2 1 из 4
Каракас 10 0 7 12 из 17 2-3
Зиген, 19-я олимпиада (на 1-й, 2-й досках) 7 0 6 10 из 13
Пальма-де-Мальорка, межзональный турнир 2 4 17 10½ из 23 14
Будапешт 3 0 11 8½ из 15 3-4
Вейк-ан-Зее 2-5
Вршац 3
1971 Стокгольм 1
1972 Умаг, чемпионат Югославии 5 0 14 12 из 19 1
Скопье, 20-я олимпиада (на 1-й, 2-й досках) 6 0 12 12 из 18
Нови-Сад 3-5
1973 Петрополис, межзональный турнир 2 1 14 9 из 17 9-10
1974 Ницца, 21-я олимпиада (на 1-й, 2-й, 3-й досках) 8 1 8 12 из 17
Амстердам 5 0 10 10 из 15 1-3
1978 Белград, чемпионат Югославии 3 0 14 10 из 17 1-2
Буэнос-Айрес, 23-я олимпиада (на 3-й, 4-й досках) 1 2 4 3 из 7
Сан-Паулу 6 2 5 8½ из 13 3-4
1979 Рио-де-Жанейро, межзональный турнир 4 2 11 9½ из 17 5-6
Лас-Пальмас 2-3
1980 Валлетта, 24-я олимпиада (на 1-й, 2-й досках) 3 0 5 5½ из 8
Сараево 4 0 11 9½ из 15 2-3
1981 Малага 2 0 9 6½ из 11 2-4
Баден-Баден 4 1 8 8 из 13 4-7
1983 Турин 1
Торремолинос 3 1 5 5½ из 9 2-3
1984 Торремолинос 2-3
Бор 6 2 5 8½ из 13 2-4
1985 Гавана 1
1986 Канн 2 0 7 5½ из 9 2-6

Изменения рейтинга

Изменения Эло[4]
Графики недоступны из-за технических проблем. См. информацию на Фабрикаторе и на mediawiki.org.

Примечания

  1. ↑ 1 2 http://chess-news.ru/node/28729
  2. ↑ 1 2 твит — 2006.
  3. ↑ 1 2 https://www.fide.com/news/1575
  4. ↑ Рейтинг Эло из списков ФИДЕ. Источники: fide.com, benoni.de, olimpbase.org

Литература

  • Шахматный словарь / гл. ред. Л. Я. Абрамов; сост. Г. М. Гейлер. — М.: Физкультура и спорт, 1964. — С. 240—241. — 120 000 экз.
  • Шахматы: энциклопедический словарь / гл. ред. А. Е. Карпов. — М.: Советская энциклопедия, 1990. — С. 131. — 621 с. — 100 000 экз. — ISBN 5-85270-005-3.
  • Линдер И. М. Ивков Борислав // Шахматная энциклопедия / И. М. Линдер, В. И. Линдер. — М. : ООО «Издательство АСТ» : ООО «Издательство Астрель», 2004. — С. 90. — 320 с. — ISBN 5-17-006939-1. — ISBN 5-271-06492-1.

Ссылки

Read other articles:

Richard III dari Inggris

Richard IIIRaja Inggris (selanjutnya...) Berkuasa26 Juni 1483 – 22 Agustus 1485Penobatan6 Juli 1483PendahuluEdward VPenerusHenry VIIInformasi pribadiPemakamanGreyfriars (Franciscan Friary), Leicester[1]WangsaWangsa YorkAyahRichard Plantagenet, Adipati YorkIbuCecily NevillePasanganAnne NevilleAnakEdward dari Middleham, Pangeran Wales Richard III (2 Oktober 1452 – 22 Agustus 1485) adalah Raja Inggris yang berkuasa selama dua tahun, dari tahun 1483 sampai kematiannya pa...

 

History of the Los Angeles Kings

The history of the Los Angeles Kings of the National Hockey League begins in 1966, as the league prepared a major expansion for the upcoming season, and awarded a new team to Los Angeles-based entrepreneur Jack Kent Cooke, who also owned the Los Angeles Lakers. While the Los Angeles Kings awaited construction to be completed on their future home, The Forum in Inglewood, California, they played their first two games during their inaugural 1967–68 season at the Long Beach Arena. The first gam...

 

Macarthur (New South Wales)

MacarthurGalat: unknown |state= value (bantuan)Perbukitan Razorback Range di antara Camden dan Picton.Jumlah penduduk233.065 (2006)LGAWollondilly, Campbelltown, CamdenDaerahSydney MetropolitanDaerah pemilihan negara bagianCampbelltown, Macquarie Fields, Camden, WollondillyDivisi FederalMacarthur, Werriwa, Hume Pemukiman di sekitar Macarthur: Western Sydney South-western Sydney South-western Sydney Blue Mountains Macarthur Southern Sydney Southern Tablelands Southern Highlands Illawarra Easter...

Circoscrizione

Disambiguazione – Se stai cercando altri significati, vedi Circoscrizione (disambigua). Questa voce o sezione sull'argomento diritto amministrativo non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Le divisioni amministrative del mondo Una circoscrizione è una parte definita di territorio di uno Stato, entro i cui confini è limitata la competenza di un...

 

Египтопитек

† Египтопитек Реконструкция внешнего вида египтопитека Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:Четвероно...

 

Punjabi calendar

Luni-solar calendar used by the Punjabi people of the Indian subcontinent Part of a series onPunjabis History Folklore Language Dialects Punjab Punjabis Nationalism DiasporaAsia Afghanistan Europe United Kingdom North America United States Canada Oceania Australia New Zealand Culture Clothing Cuisine Dance Festivals (India • Pakistan) Literature Media Music Religion (Folk religion) Sport Television Regions Majha Malwa Doaba Puadh Bagar Pothwar Derajat Bhatiore Bhattiana Chhachh Kachhi Doabs...

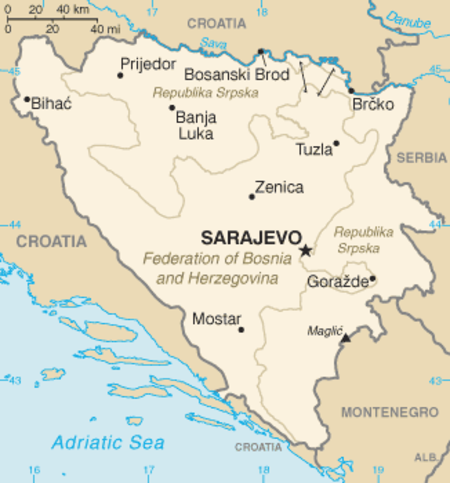
Resolusi 824 Dewan Keamanan Perserikatan Bangsa-Bangsa

Resolusi 824Dewan Keamanan PBBBosnia dan HerzegovinaTanggal6 Mei 1993Sidang no.3.208KodeS/RES/824 (Dokumen)TopikBosnia dan HerzegovinaRingkasan hasil15 mendukungTidak ada menentangTidak ada abstainHasilDiadopsiKomposisi Dewan KeamananAnggota tetap Tiongkok Prancis Rusia Britania Raya Amerika SerikatAnggota tidak tetap Brasil Tanjung Verde Djibouti Spanyol Hungaria Jepang Maroko Selandia Baru Pakistan Venezuel...

 

Submersion (coastal management)

Aspect of coastal erosion Submersion is the sustainable cyclic portion of coastal erosion where coastal sediments move from the visible portion of a beach to the submerged nearshore region, and later return to the original visible portion of the beach.[1] The recovery portion of the sustainable cycle of sediment behaviour is named accretion. Submersion vs erosion The sediment that is submerged during rough weather forms landforms including storm bars. In calmer weather waves return se...

 

Dṛg-Dṛśya-Viveka

Part of a series onAdvaita SchoolsClassical Advaita Vedanta Bhāmatī Vivarana Shaivism/Tantra/Nath Kashmir Shaivism (Pratyabhijna) Nath (Inchegeri Sampradaya) New movements Neo-Advaita Nondualism ConceptsClassical Advaita vedanta Atman Brahman Avidya Ajativada Mahāvākyas Satchitananda Om Tat Tvam Asi Three Bodies Aham Cause and effect Kosha Neti neti Kashmir Shaivism Pratyabhijna so'ham Practices Guru Meditation Svādhyāya Sravana, manana, nididhyasana Jnana yoga Rāja yoga Unfoldment of ...

Direktorat Jenderal Pembangunan Kawasan Perdesaan

Direktorat Jenderal Pembangunan Kawasan Perdesaan Kementerian Desa, Pembangunan Daerah Tertinggal, dan Transmigrasi Republik IndonesiaGambaran umumDasar hukumPeraturan Presiden Nomor 12 Tahun 2015Susunan organisasiDirektur JenderalIr. Harlina Sulistyorini, M.SiSitus webkemendesa.go.id Direktorat Jenderal Pembangunan Kawasan Perdesaan merupakan unsur pelaksana pada Kementerian Desa, Pembangunan Daerah Tertinggal, dan Transmigrasi Republik Indonesia yang berada di bawah dan bertanggung jaw...

 

فعل خبري

تحتاج هذه المقالة كاملةً أو أجزاءً منها لإعادة الكتابة حسبَ أسلوب ويكيبيديا. فضلًا، ساهم بإعادة كتابتها لتتوافق معه. (أبريل 2019) تحتاج النصوص المترجمة في هذه المقالة إلى مراجعة لضمان معلوماتها وإسنادها وأسلوبها ومصطلحاتها ووضوحها للقارئ، لأنها تشمل ترجمة اقتراضية أو غير س...

 

العلاقات التشيلية الكوبية

العلاقات التشيلية الكوبية تشيلي كوبا   تشيلي   كوبا تعديل مصدري - تعديل   العلاقات التشيلية الكوبية هي العلاقات الثنائية التي تجمع بين تشيلي وكوبا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة تشيلي كوبا المس�...

Sophie Paris

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. PT Sophie Paris IndonesiaNama dagangSophie ParisJenisPerusahaan swastaIndustriModeDidirikan1995PendiriBruno HassonKantorpusatJl. Adyaksa Raya No. 33, Lebak Bulus-Jakarta Selatan, IndonesiaWilayah operasiAsia Tenggara, MarokoTokohkunciBruno Hasson (Pres...

 

Frances Cleveland

First Lady of the United States (1886–1889, 1893–1897) Frances Cleveland1886 portraitFirst Lady of the United StatesIn roleMarch 4, 1893 – March 4, 1897PresidentGrover ClevelandPreceded byMary Harrison McKee (acting)Succeeded byIda Saxton McKinleyIn roleJune 2, 1886 – March 4, 1889PresidentGrover ClevelandPreceded byRose Cleveland (acting)Succeeded byCaroline Harrison Personal detailsBornFrances Clara Folsom(1864-07-21)July 21, 1864Buffalo, New York, U.S.DiedOctober ...

 

Ringdown

Not to be confused with Quik Call I. Ring Off redirects here. For the song, see Ring Off (song). For the astronomical phenomenon, see Binary black hole This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (June 2022) (Learn how and when to remove this message) In telephony, ringdown is a method of signaling an operator in which telephone ringing current is sent ove...

Le Vieil-Évreux

Le Vieil-Évreuxcomune (dettagli) Le Vieil-Évreux – Veduta LocalizzazioneStato Francia Regione Normandia Dipartimento Eure ArrondissementÉvreux CantoneÉvreux-3 TerritorioCoordinate49°00′N 1°14′E49°00′N, 1°14′E (Le Vieil-Évreux) Superficie11,52 km² Abitanti758[1] (2009) Densità65,8 ab./km² Altre informazioniCod. postale27930 Fuso orarioUTC+1 Codice INSEE27684 CartografiaLe Vieil-Évreux Modifica dati su Wikidata · Manuale Le Vieil-Évreux ...

 

Comtés du Commonwealth de Pennsylvanie

Le Commonwealth de Pennsylvanie, un des 50 États américains, est divisé en 67 comtés (counties). Liste des comtés Adams - Siège : Gettysburg. Allegheny - Siège : Pittsburgh. Armstrong - Siège : Kittanning. Beaver - Siège : Beaver. Bedford - Siège : Bedford. Berks - Siège : Reading. Blair - Siège : Hollidaysburg. Bradford - Siège : Towanda. Bucks - Siège : Doylestown. Butler - Siège : Butler. Cambria - Siège : Ebensburg. C...

 

JADE (programming language)

Software development and deployment platform This article is about the end-to-end development environment. For the Java middleware, see Java Agent Development Framework. For the Pug (formerly Jade) Javascript templating engine, see Comparison of web template engines. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs to be updated. Relevant discussion may be found on the t...

Isao Nakajima

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

 

Weichmacher

Der Weichmacher aus dem Radiergummi ist in das rote Plastikrohr eingewandert und hat es zum Schmelzen gebracht. Weichmacher bzw. Weichmachungsmittel (englisch plasticizer) bewirken, dass Stoffe weicher, flexibler, geschmeidiger und elastischer sind. Weichmacher wirken als Lösungsmittel. Sie lassen Kunststoffe aufquellen und überführen sie in einen gelartigen Zustand. Wenn Weichmacher wieder entweichen, schrumpft der Stoff, wird spröder, härter und gegebenenfalls rissig.[1] Ein be...