Граф Пэли
| |||||||||||||||||
Read other articles:

Aishwarya SharmaLahir08 Desember 1992 (umur 31)Ujjain, Madhya Pradesh, IndiaKebangsaanIndianPekerjaanaktrisTahun aktif2015–sekarangDikenal atasGhum Hai Kisikey Pyaar MeiinSuami/istriNeil Bhatt (m. 2021) Aishwarya Sharma (lahir 08 Desember 1992) adalah seorang aktris televisi India yang dikenal karena perannya sebagai Patralekha Salunkhe di Ghum Hai Kisikey Pyaar Meiin.[1] Kehidupan pribadi Sharma bertemu dengan aktor Neil Bhatt di lokasi syu...

Administrative division of Venezuela DependenciesFederal Dependencies of Venezuela Dependencias Federales de VenezuelaDependencies FlagLocation in VenezuelaCreated1938Islands and Groups List Aves Island (Isla de Aves)Las Aves Archipelago (Archipiélago Las Aves)La Blanquilla Island (Isla La Blanquilla)Los Frailes Archipelago (Archipiélago Los Frailes)La Sola Island (Isla La Sola)Patos Island (Isla de Patos)Los Hermanos Archipelago (Islas Los Hermanos)Los Monjes Archipelago (Archipiélago Los...

Municipality in Batangas, Philippines For the other places named San Jose in the Philippines, see San Jose (disambiguation).This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: San Jose, Batangas – news · newspapers · books · scholar · JSTOR (November 2013) (Learn how and when to remove this template message) Mun...

Jenazah-jenazah pasukan Paraguay seusai Pertempuran Boquerón, Juli 1866. Paraguay mengalami kekalahan total dalam Perang Paraguay. Istilah debellatio (bahasa Inggris: debellation; berasal dari bahasa Latin: bellum, artinya mengalahkan, atau tindakan menaklukkan atau menundukkan, secara harfiah, berperang hingga (musuh) turun) merujuk kepada akhir perang yang disebabkan oleh kehancuran total dari negara yang terlibat dalam perang. Profesor hukum Israel Eyal Benvenisti mendefinisikannya sebaga...

Questa voce sull'argomento calciatori italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Livio Risso Nazionalità Italia Calcio Ruolo Centrocampista Termine carriera 1949 Carriera Squadre di club1 1939-1940 Dopolavoro Pirelli? (?)1941-1945 Lazio1 (0)1945 Bari? (?)1945-1946 Italia Libera? (?)1946-1948 Civita Castellana? (?)1949-1950 Romulea? (?)1950-1951 STEFER ...

Jaramogi Oginga Odinga Wakil Presiden Kenya 1Masa jabatan12 Desember 1964 – 14 April 1966PresidenJomo KenyattaPenggantiJoseph Murumbi Informasi pribadiLahirObadiah AdonijahOktober 1911 (1911-10)Bondo, Afrika Timur BritaniaMeninggal20 Januari 1994(1994-01-20) (umur 82)Nairobi, KenyaPartai politik List Kenya African Union (1948–1959)Kenya African National Union (1960–1966)Kenya People's Union (1966–1990)Forum for the Restoration of Democracy(1991)Forum for the Res...

Nama ini menggunakan cara penamaan Spanyol: nama keluarga pertama atau paternalnya adalah Paterno dan nama keluarga kedua atau maternalnya adalah de Vera Ignacio. Pedro Alejandro Paterno Pedro Alejandro Paterno y de Vera Ignacio[1][note 1] (27 Februari 1857 – 26 April 1911[note 2][2]) adalah seorang politikus Filipina. Ia juga merupakan seorang penyair dan novelis.[3] Lihat pula Dolores Paterno Catatan ^ Juga disebut Pedro Alejandro...

Questa voce sull'argomento stagioni delle società calcistiche spagnole è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Voce principale: Real Sporting de Gijón. Real Sporting de GijónStagione 2019-2020Sport calcio SquadraReal Sporting de Gijón Allenatore José Alberto López Menéndez (fino al 21 dicembre) Miroslav Đukić (fino al 20 luglio) David Gallego Presidente Javier Fernández Segunda División13º posto Coppa del RePrimo turno StadioStadio...

15th Bombardment Squadron redirects here. For the 15th Bombardment Squadron, Very Heavy, see 15th Special Operations Squadron. 915th Air Refueling SquadronBoeing KC-135A Stratotanker as flown by the 915th Air Refueling SquadronActive1940–1943; 1958–1971Country United StatesBranch United States Air ForceRoleAir refuelingEngagementsAmerican Theater of World War IIEuropean Theater of World War IIDecorationsAir Force Outstanding Unit AwardInsigniaPatch with 915th Air Refueling Squad...
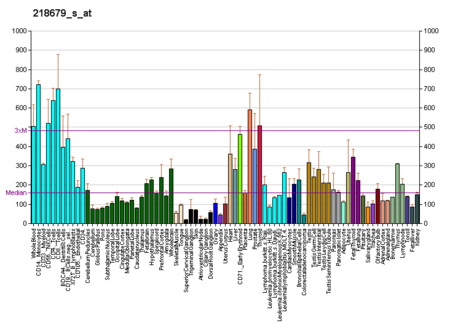
VPS28 المعرفات الأسماء المستعارة VPS28, ESCRT-I subunit, subunit of ESCRT-I معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 611952 MGI: MGI:1914164 HomoloGene: 69205 GeneCards: 51160 علم الوجود الجيني الوظيفة الجزيئية • GO:0032403 protein-containing complex binding• ubiquitin binding• GO:0001948، GO:0016582 ربط بروتيني المكونات الخلوية • سيتوب...

الدوري الإنجليزي الدرجة الأولى 2018–19 تفاصيل الموسم دوري كرة القدم الإنجليزي 2018–19 النسخة 92 البلد المملكة المتحدة التاريخ بداية:4 أغسطس 2018 نهاية:4 مايو 2019 المنظم دوري كرة القدم الإنجليزية البطل نادي لوتون تاون مباريات ملعوبة 552 عدد المشاركين 24 ...

2017 European Athletics U23 ChampionshipsTrack events100 mmenwomen200 mmenwomen400 mmenwomen800 mmenwomen1500 mmenwomen5000 mmenwomen10,000 mmenwomen100 m hurdleswomen110 m hurdlesmen400 m hurdlesmenwomen3000 msteeplechasemenwomen4 × 100 m relaymenwomen4 × 400 m relaymenwomenRoad events20 km walkmenwomenField eventsHigh jumpmenwomenPole vaultmenwomenLong jumpmenwomenTriple jumpmenwomenShot putmenwomenDiscus throwmenwomenHammer throwmenwomenJavelin throwmenwomenCombined eventsHeptathlonwome...

Ethnic group This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: German Australians – news · newspapers · books · scholar · JSTOR (July 2023) (Learn how and when to remove this message) Ethnic group German AustraliansDeutsch-AustralierTotal population1,026,138 (by ancestry, 2021)[1](4% of the Australian ...

Сграффито на греческом доме острова Хиос Улочка на греческом острове Хиос относится к Мастихохория[англ.] Сграффи́то (итал. sgraffito), или граффи́то (итал. graffito — процарапанный), — техника изображения и разновидность декорирования, которая заключается в нанесении...

Pakistan Army infantry unit 1st Battalion, Azad Kashmir RegimentFounded6 October 194720 September 1971Country PakistanBranch Pakistan ArmyRoleInfantrySize1 battalionPart of111th Infantry BrigadeEngagementsIndo-Pakistani War of 1947Indo-Pakistani War of 1965Indo-Pakistani War of 1971CommandersPrevious commanderLieutenant-Colonel Nausherwan Khan[1]Military unit The 1st Battalion, Azad Kashmir Regiment is an infantry battalion of the Azad Kashmir Regiment of the Pakistan A...

Questa voce sull'argomento strade degli Stati Uniti d'America è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. U.S. Route 80LocalizzazioneStato Stati Uniti Stati federati Georgia Alabama Mississippi Louisiana Texas DatiClassificazioneStrada statale InizioIsola Tybee (Georgia) FineDallas Lunghezza1.661 km DirezioneEst-ovest Data apertura1926 PercorsoPrincipali intersezioni Georgia State Route 26 a Isola Tybee (GA) Interstat...

Nota: Para outros significados, veja Gália (desambiguação). Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências (Encontre fontes: ABW • CAPES • Google (N • L • A)). (Dezembro de 2022) Provincia Gallia LugdunensisProvíncia Gália Lugdunense Província do(a) Império Romano ← 27 a.C.–297 → → → → Gália Lugdunense, c. 400 Capital Lugduno Líder L...

Houssine KharjaKharja con la nazionale marocchina nel 2009Nazionalità Francia Marocco (dal 2003) Altezza181 cm Peso77 kg Calcio RuoloCentrocampista Termine carriera1º luglio 2016 - giocatore CarrieraGiovanili 1998-2000 Paris Saint-Germain2000-2001 Sporting Lisbona Squadre di club1 2001-2005 Ternana119 (9)2005-2006→ Roma12 (1)2006-2007 Ternana0 (0)2007-2008 Piacenza17 (2)2008-2009 Siena51 (8)2009-2011 Genoa20 (3)2011→ Inter15 (1)20...

「G104」重定向至此。关于高速铁路列车车次,请见「京沪高速动车组列车」。 39°26′00″N 116°51′36″E / 39.4332032°N 116.8599696°E / 39.4332032; 116.8599696 104国道104国道路綫圖G104宁德段道路信息道路總長2,606公里(1,619英里)主要连接道路起點北京市东城区永定门桥[1]終點福建省福州市平潭县东兴村村委会附近公路系統中华人民共和国国道 104国道(�...

هجرة بني هلالملف:راية بنو هلال.pngراية بنو هلالفارس عربيمعلومات عامةالفترة الزمنية 440 هـمناطق الوجود المميزةبلد الأصل نجد الحجاز شمال افريقيا شمال افريقيااللغاتاللغة الأم العربيةالدين الإسلامالمجموعات العرقية المرتبطةفرع من العربهوامش تشكلت التغريبة الهلالية من عدة قب...








