GW-–њ—А–Є–±–ї–Є–ґ–µ–љ–Є–µ
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Jalanan di Stevensville, Michigan Stevensville adalah sebuah desa di Berrien County di negara bagian Michigan, AS. Desa ini terletak di dalam Lincoln Township. Populasinya adalah 1.142 pada sensus 2010. Sejarah Desa itu dilapisi pada tahun 1840-an oleh...

Aurelia aurita Aurelia aurita di Laut Merah Status konservasi Tidak dievaluasi (IUCN 3.1) Klasifikasi ilmiah Kerajaan: Animalia Filum: Cnidaria Kelas: Scyphozoa Ordo: Semaeostomeae Famili: Ulmaridae Genus: Aurelia Spesies: A. aurita Nama binomial Aurelia auritaLinnaeus, 1758 Sinonim[1] Aurellia flavidula Peron & Lesueur, 1810 Medusa aurita Linnaeus, 1758 Medusa purpurea Pennant, 1777 Aurelia aurita (juga dikenal dengan ubur-ubur bulan) adalah spesies di dalam famili Ulm...
Hohenau Lambang kebesaranLetak Hohenau NegaraJermanNegara bagianBayernWilayahNiederbayernKreisFreyung-GrafenauSubdivisions20 ortsteilPemerintahan вАҐ MayorEduard Schmid (CSU)Luas вАҐ Total43,12 km2 (1,665 sq mi)Ketinggian804 m (2,638 ft)Populasi (2013-12-31)[1] вАҐ Total3.326 вАҐ Kepadatan0,77/km2 (2,0/sq mi)Zona waktuWET/WMPET (UTC+1/+2)Kode pos94545Kode area telepon08558Pelat kendaraanFRGSitus webwww.hohenau....

Questa voce sull'argomento storia del diritto è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Il preambolo della Carta dei diritti fondamentali dell'Unione europea Le libertà individuali (art.13 costituzione italiana) sono l'insieme delle libertà proprie di ogni individuo. I primi teorici di questo tipo di libertà si perdono nel tempo, ma furono i liberali inglesi del XVII-XVIII secolo, tra cui spicca il nome di John Locke, a classificarli e razion...

A questa voce o sezione va aggiunto il template sinottico {{Militare}} Puoi aggiungere e riempire il template secondo le istruzioni e poi rimuovere questo avviso. Se non sei in grado di riempirlo in buona parte, non fare nulla; non inserire template vuoti. Luchino Dal Verme Luchino Dal Verme (Milano, 25 novembre 1913 вАУ Torre degli Alberi, 29 marzo 2017) √® stato un militare e partigiano italiano. Stemma dei Dal Verme Indice 1 Biografia 2 Note 3 Bibliografia 4 Voci corre...

Marco van Basten, vincitore del Pallone d'oro 1989 LвАЩedizione 1989 del Pallone d'oro, 34¬™ edizione del premio calcistico istituito dalla rivista francese France Football, fu vinta dall'olandese Marco van Basten (Milan). I giurati che votarono furono 27, provenienti da Albania, Austria, Belgio, Bulgaria, Cecoslovacchia, Danimarca, Finlandia, Francia, Germania Est, Germania Ovest, Grecia, Inghilterra, Irlanda, Italia, Jugoslavia, Lussemburgo, Paesi Bassi, Polonia, Portogallo, Romania, Scozia...

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Lambang Iran вАУ berita ¬Ј surat kabar ¬Ј ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of Algerian films вАУ news ¬Ј newspapers ¬Ј books ¬Ј scholar ¬Ј JSTOR (October 2023) (Learn how and when to remove this message) Part of a series on theCulture of Algeria HistoryMaritime history вАҐ Military history вАҐ Economic history People LanguagesArabic пњљ...

2005 American filmThe Prize Winner of Defiance, OhioTheatrical release posterDirected byJane AndersonWritten byJane AndersonBased onThe Prize Winner of Defiance, Ohio: How My Mother Raised 10 Kids on 25 Words or Lessby Terry RyanProduced byJack RapkeSteve StarkeyRobert ZemeckisStarringJulianne MooreWoody HarrelsonLaura DernCinematographyJonathan FreemanEdited byRobert DalvaMusic byJohn FrizzellProductioncompaniesRevolution StudiosImageMoversDistributed byGo Fish Pictures[1] (through D...

Plane crash on 19 February 1985 Iberia Flight 610An Iberia Boeing 727-200 similar to the one involvedAccidentDate19 February 1985 (1985-02-19)SummaryControlled flight into terrain due to pilot errorSiteMount Oiz, Biscay, near Bilbao Airport, Spain 43¬∞13вА≤43вА≥N 02¬∞35вА≤24вА≥W / 43.22861¬∞N 2.59000¬∞W / 43.22861; -2.59000AircraftAircraft typeBoeing 727вАУ256Aircraft nameAlhambra de GranadaOperatorIberiaRegistrationEC-DDUFlight originMadridвАУ...

Swedish-speaking minority of Estonia Estonian SwedesRegions with significant populations Sweden26,000[1] Estonia811[2]LanguagesEstonian Swedish, EstonianReligionHistorically LutheranismPredominantly irreligiousRelated ethnic groupsFinland-Swedes, Swedes, Baltic Germans Swedish towns and villages in Western Estonia Swedish church in Hullo, Vormsi The Estonian Swedes, or Estonia-Swedes (Swedish: estlandssvenskar, colloquially aibofolke, island people; Estonian: eestiro...

American politician Frank DenholmMember of the U.S. House of Representativesfrom South Dakota's 1st districtIn officeJanuary 3, 1971 вАУ January 3, 1975Preceded byBen Lone Feather ReifelSucceeded byLarry Pressler Personal detailsBornFranklin Edvard Denholm(1923-11-29)November 29, 1923Day County, South Dakota, U.S.DiedApril 7, 2016(2016-04-07) (aged 92)Brookings, South Dakota, U.S.Political partyDemocraticAlma materSouth Dakota State UniversityUniversity of South Dako...

Olaug NilssenBiographieNaissance 28 d√©cembre 1977 (46 ans)F√ЄrdeNationalit√© norv√©gienneFormation Universit√© de BergenActivit√© √ЙcrivaineAutres informationsDistinctions Liste d√©taill√©eSigmund Skard Fellowship (2004)Fonds du p√®re Alfred Andersson-Rysst (2004)Language Prize (d) (2006)Prix de la litt√©rature nynorske (2017)Prix Dobloug (2019)Prix Fritt-Ord (en) (2021)modifier - modifier le code - modifier Wikidata Olaug Nilssen, n√©e le 28 d√©cembre 1977 √† F√Єrde, est un romanci√®re...

1953 film To Be Without WorriesDirected byGeorg MarischkaWritten byJohann Nestroy (play) Georg Marischka Hans WeigelProduced byG√Љnther StapenhorstStarringWalter M√Љller Hans Moser Walter KochCinematographyFriedl Behn-GrundEdited byIrene TomschikMusic byOscar StrausProductioncompanyCarlton FilmDistributed byInternational FilmRelease date 22 May 1953 (1953-05-22) Running time88 minutesCountriesAustria West GermanyLanguageGerman To Be Without Worries (German: Einmal keine Sorgen ...

History of the Seattle Seahawks, an American football team in the National Football League The Seattle Seahawks are a professional American football team organized in 1976 and based in Seattle, Washington, US, that plays in the National Football League. This article details the history of the Seattle Seahawks American football club. Overview As one of the agreed parts of the 1970 AFLвАУNFL Merger, the NFL began planning to expand from 26 to 28 teams.[1] Ralph Wilson was the first to p...

Spanish tennis player (born 1972) For another tennis player born 1976, see Conchita Martínez Granados. In this Spanish name, the first or paternal surname is Martínez and the second or maternal family name is Bernat . Conchita MartínezConchita Martínez at the 2010 US OpenFull nameInmaculada Concepción Martínez BernatCountry (sports) SpainResidenceBarcelona, SpainBorn (1972-04-16) 16 April 1972 (age 52)Monzón, Huesca, SpainHeight1.73 m (5 ft 8 ...
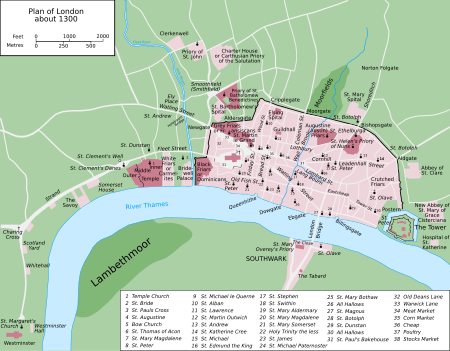
–£ —Н—В–Њ–≥–Њ —В–µ—А–Љ–Є–љ–∞ —Б—Г—Й–µ—Б—В–≤—Г—О—В –Є –і—А—Г–≥–Є–µ –Ј–љ–∞—З–µ–љ–Є—П, —Б–Љ. –°–Є—В–Є (–Ј–љ–∞—З–µ–љ–Є—П). –Ы–Њ–љ–і–Њ–љ—Б–Ї–Є–є —Б–Є—В–Є–∞–љ–≥–ї. City of London –Т–Є–і –љ–∞ –≤–Њ—Б—В–Њ—З–љ—Г—О —З–∞—Б—В—М –°–Є—В–Є —Б —О–ґ–љ–Њ–≥–Њ –±–µ—А–µ–≥–∞ –Ґ–µ–Љ–Ј—Л 51¬∞30вА≤55вА≥ —Б. —И. 00¬∞05вА≤31вА≥ –Ј. –і.HG–ѓO –У–Њ—А–Њ–і –Ы–Њ–љ–і–Њ–љ –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Є–≤–љ—Л–є –Њ–Ї—А—Г–≥ –≥–Њ—А–Њ–і–∞ –°–Є—В–Є –Ф–∞—В–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є—П –Њ–Ї–Њ–ї–Њ 47 –≥–Њ–і–∞ –љ. —Н. –Эпњљ...

Superligaen Land Denemarken Bond DBU Competitie Superligaen Seizoensdetails Seizoen 2012/13 Kampioen FC Kopenhagen (10e titel) Topscorer(s) Andreas Cornelius (18 goals) Aantal clubs 12 Degradatie naar 1. Division Gedegradeerd Silkeborg IF, AC Horsens Europese kwalificatie FC Kopenhagen (CL), FC Nordsjælland (CL), Randers FC (EL), Esbjerg fB (EL) Algemeen Opgericht 1991 Recordtitelhouder FC Kopenhagen (10x) Website Superliga.dk Actueel Superligaen 2015/16 Navigatie Vorige &#...

Nyala Macho HembraEstado de conservaci√≥nPreocupaci√≥n menor (UICN 3.1)[1]Taxonom√≠aReino: AnimaliaFilo: ChordataClase: MammaliaOrden: ArtiodactylaFamilia: BovidaeG√©nero: TragelaphusEspecie: T. angasiiGray, 1849Distribuci√≥n Distribuci√≥n del nyala[editar datos en Wikidata] El Tragelaphus angasii, de nombre com√Їn nyala (cuya transcripci√≥n fon√©tica al espa√±ol es √±ala), es una especie de mam√≠fero artiod√°ctilo de la familia Bovidae.[2] Es un ant√≠lope african...

This article needs to be updated. Please help update this article to reflect recent events or newly available information. (June 2024)This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (August 2015) (Learn how and when to remove this message)The Educational Global Climate Model or EdGCM is a fully functional global climate model...















