Условия Каруша — Куна — Таккера
|
Read other articles:

Class of compounds AntiprogestogenDrug classMifepristone, an antiprogestogen that is used to induce medical abortions.Class identifiersSynonymsAntiprogestins; Progesterone antagonists; Progesterone blockersUseMedical abortion, emergency contraception, uterine fibroidsATC codeG03XBBiological targetProgesterone receptorChemical classSteroidalLegal statusIn Wikidata Antiprogestogens, or antiprogestins, also known as progesterone antagonists or progesterone blockers, are a class of drugs which pr...

Untuk kegunaan lain, lihat Aceh (disambiguasi). Koordinat: 2°20′N 97°50′E / 2.333°N 97.833°E / 2.333; 97.833 Kabupaten Aceh SingkilKabupatenTranskripsi bahasa daerah • Jawoe/Jawiاچيه سيڠكيلTari Dampeng Aceh Singkil LambangMotto: Sekata sepekat(Singkil) Harmonisasi persaudaraan dan toleransiPetaKabupaten Aceh SingkilPetaTampilkan peta SumatraKabupaten Aceh SingkilKabupaten Aceh Singkil (Indonesia)Tampilkan peta IndonesiaKoordinat:...
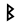
此條目介紹的是拉丁字母中的第2个字母。关于其他用法,请见「B (消歧义)」。 提示:此条目页的主题不是希腊字母Β、西里尔字母В、Б、Ъ、Ь或德语字母ẞ、ß。 BB b(见下)用法書寫系統拉丁字母英文字母ISO基本拉丁字母(英语:ISO basic Latin alphabet)类型全音素文字相关所属語言拉丁语读音方法 [b][p][ɓ](适应变体)Unicode编码U+0042, U+0062字母顺位2数值 2歷史發...

American attorney and anti-vaccine activist (born 1954) Robert F. Kennedy Jr.Kennedy in 2023BornRobert Francis Kennedy Jr. (1954-01-17) January 17, 1954 (age 70)Washington, D.C., U.S.EducationHarvard University (BA)London School of EconomicsUniversity of Virginia (JD)Pace University (LLM)Occupation(s)Environmental lawyerWriterAnti-vaccine activistNotable workThe Riverkeepers (1997)Crimes Against Nature (2004)The Real Anthony Fauci (2021)A Letter to Liberals (2022)Political partyIndepende...

مخرج أفلامالمخرج المصري محمود ذو الفقار في ستوديو أحد أفلامه في سنة 1968.التسمية للأنثى مخرجة أفلام فرع من مخرج[1]فنان تشكيليfilm professional (en) film crew member (en) النوع مهن السينما المجال إخراج الأفلام تعديل - تعديل مصدري - تعديل ويكي بيانات صورة لفيلم أثناء إخراجه الإخراج[2] في أب...

ManimiL'area verde (ovvero l'attuale Slesia) rappresenta la cultura di Przeworsk identificata con i Lugi al principio del I secolo. L'area viola scura è l'impero romano. Nomi alternativiMolti archeologi identificano i Lugi con la cultura di Przeworsk Sottogruppidei Lugi ne facevano parte: gli Arii, gli Elisi, gli Elveconi, i Manimi e i Naarvali[1] Luogo d'origineEuropa centrale, a nord dei Sudeti PeriodoDall'inizio del IV secolo a.C. LinguaLingue germaniche Distribuzione Ge...

Norman Fucking Rockwellsingolo discograficoScreenshot tratto dal video del branoArtistaLana Del Rey Pubblicazione1º novembre 2019 Durata4:09 Album di provenienzaNorman Fucking Rockwell! GenerePop EtichettaPolydor, Interscope ProduttoreLana Del Rey, Jack Antonoff RegistrazioneConway Recording Studios (Los Angeles) e House of Breaking Glass (Seattle) FormatiDownload digitale, streaming CertificazioniDischi d'argento Regno Unito[1](vendite: 200 000+) Lana Del Rey - cronol...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Le tre spartizioni della Polonia Con spartizioni della Polonia (in polacco Rozbiór Polski o Rozbiory Polski; in lituano Padalijimas) si fa riferimento alle divisioni della Confederazione polacco-lituana alla fine del XVIII secolo avvenute in tre differenti occasioni (1772, 1793 e 1795) ad opera delle potenze confinanti rappresentate dall'Impero russo, dal Regno di Prussia e della Monarchia asburgica.[1] In tutti questi casi ci furono assicurazioni riguardo al riconoscimento...

English Professor of Hebrew and Divinity For the New Zealand rugby union player, see Alexander Kirkpatrick (rugby union). Memorial to Alexander Francis Kirkpatrick in Ely Cathedral Alexander Francis Kirkpatrick (25 June 1849 – 22 January 1940) was Regius Professor of Hebrew at Cambridge University (1882–1903) and the third Master of Selwyn College, Cambridge (1898–1907). Life Kirkpatrick was born at Lewes, East Sussex, only son (with three daughters) of Rev. Francis Kirkpatrick, and was...

أكتوبامين الاسم النظامي (RS)-4-(2-amino-1-hydroxy-ethyl)phenol اعتبارات علاجية مرادفات OCT, Norsympathol, Norsynephrine, para-Octopamine, beta-Hydroxytyramine, para-hydroxy-phenyl-ethanolamine بيانات دوائية استقلاب (أيض) الدواء N-أسيتيل ترانسفيريزs; ناقلة N-ميثيل فينيل إيثانولامين معرّفات CAS 104-14-3 ك ع ت C01CA18 بوب كيم CID 4581 IUPHAR 2149 ECHA InfoCard ID...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2016) عملية المناظير جزء من ثورة التحرير الجزائرية التاريخ وسيط property غير متوفر. بداية يوليو 1959 نهاية ما�...

1985 single by Giorgio Moroder and Philip OakeyGood-Bye Bad TimesSingle by Giorgio Moroder and Philip Oakeyfrom the album Philip Oakey & Giorgio Moroder Released10 June 1985[1]Recorded1985Length3:42LabelVirgin RecordsSongwriter(s)Oakey and MoroderProducer(s)Giorgio MoroderGiorgio Moroder singles chronology Shannon's Eyes (1985) Good-Bye Bad Times (1985) Be My Lover Now (1985) Philip Oakey singles chronology Together in Electric Dreams(1984) Good-Bye Bad Times(1985) Be My ...

Исидор Севильский в книге «Этимологии» о апеллианах. Рукопись XIII века. Национальная библиотека Франции Апеллиа́не или апелли́ты (др.-греч. ἀπελλιανοί; лат. apellitæ; др.-рус. аполианє) — христианское течение гностического характера II века, названное по имени основателя их...

El Erecteón en la Acrópolis. Fachada sur. El Erecteón o Erecteion (en griego Ἐρέχθειον) es un templo griego creado por los arquitectos Mnesicles y Filocles, y Alcámenes como creador de las Cariátides este templo está situado en el lado norte de la Acrópolis de Atenas en frente al Templo de Atenea Niké, fue creado en honor a los dioses Atenea Polias y Poseidón y a Erecteo, rey mítico de la ciudad. Su nombre significa el (templo) de Erecteo. De orden jónico, áptero, atribu...

Johann Gottfried Herder BiografiKelahiran25 Agustus 1744 Morąg (Kerajaan Prusia) Kematian18 Desember 1803 (59 tahun)Weimar (Kekaisaran Romawi Suci) Tempat pemakamanSt. Peter und Paul (en) Galat: Kedua parameter tahun harus terisi! Data pribadiAgamaGereja Lutheran PendidikanUniversitas Königsberg KegiatanSpesialisasiFilsafat pikiran, filsafat bahasa dan filsafat politik Pekerjaanfilsuf, kritikus sastra, literary scholar (en) , penulis opini, penulis, penyair, penerjem...

Proposed personal rapid transit network This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Shweeb – news · newspapers · books · scholar · JSTOR (September 2015) (Learn how and when to remove this message) A single Shweeb car Shweeb is a proposed personal rapid transit network in New Zealand, based on human-powe...

Novelist, children's literature (born 1964) PJ HaarsmaPJ Haarsma at the 2015 Comic ConBornPhilip-Jon Haarsma (1964-06-05) June 5, 1964 (age 60)Georgetown, Ontario, CanadaOccupationProducer, novelistCitizenshipDual citizen of Canada and United StatesPeriod2004–presentGenreYoung adult science fictionNotable worksThe Softwire Series:Virus on Orbis 1Betrayal on Orbis 2Wormhole Pirates on Orbis 3Awakening on Orbis 4Notable awardsABC New Voices in Children's Literature Award 2008 The Softwir...

Questa voce o sezione sull'argomento gruppi musicali è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti più precisamente. Segui i suggerimenti del progetto di riferimento. Unkle Paese d'origine Inghilt...

Corbeille à anse Unicode V31 {{{trans}}} Version hiéroglyphique et hiératique La corbeille à anse est un caractère unilitère hiéroglyphique égyptien classé dans la section V « Cordes, fibres, corbeilles, sacs » de la liste de Gardiner, noté V31. Il représente une corbeille avec une anse. Il ne doit pas être confondu avec le bilitère neb, représenté sous la forme d’une corbeille sans anse. Il est translittéré k. Exemples de mots Ce caractère est utilisé comme ...














