Теорема о верхней границе
|
Read other articles:

Ann RichardsLahirShirley Ann Richards(1917-12-13)13 Desember 1917Sydney, AustraliaMeninggal25 Agustus 2006(2006-08-25) (umur 88)Torrance, California, A.STahun aktif1937–1960Suami/istriEdmond Angelo (1949–1983) (wafat) (3 anak)AnakJuliet, Christopher, Mark Shirley Ann Richards (13 Desember 1917 – 25 Agustus 2006) adalah seorang aktris dan penulis Australia, yang mencapai ketenaran dalam serangkaian film Australia tahun 1930-an untuk Ken G. Hall sebelum pindah ke ...

Marie RøpkeInformasi pribadiKebangsaan DenmarkLahir19 Juni 1987 (umur 36)Tempat tinggalCopenhagen, DenmarkTinggi176 m (577 ft 5 in)[1]PeganganKananGanda putri & campuranPeringkat tertinggi14 (WD) 12 Jan 201275 (XD) 21 Jan 2010Profil di BWF Marie Røpke (lahir 19 Juni 1987) adalah seorang pemain Bulutangkis asal Denmark.[2][3] Ibunya Lene Køppen memenangkan tunggal putri pada Kejuaraan bulu tangkis dunia pertama pada tahun 1977 dan merupak...

Itang YunaszLahirYusjirwan Yunasz31 Desember 1958 (umur 65)Jakarta, IndonesiaNama lainItang YunaszPekerjaanAktorPenyanyiPerancang busanaTahun aktif1981 - sekarangSuami/istriYeni Mulyani (m. 1998)Anak Muhammad Daffa Ramada Najla Kamila Orang tuaYunas Sutan Pengeran (ayah) Yuliana Farahdibha (ibu)KerabatSiti Hafar Raihaanun Nabila (keponakan) Yusjirwan Yunasz atau yang lebih dikenal dengan Itang Yunasz (lahir 31 Desember 1958) adalah seorang aktor,...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. Будь ласка, допоможіть удосконалити цю статтю, додавши посилання на надійні (авторитетні) джерела. Зверніться на сторінку обговорення за поясненнями та допоможіть виправити недоліки. Мат...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Cristian Boscolo Nazionalità Italia Calcio Ruolo Centrocampista Termine carriera 2009 CarrieraSquadre di club1 1990-1996 Como89 (1)1996-1997→ Lecco13 (1)1996-1997 Como10 (0)1997-2001 Lumezzane120 (0)2001-2002 Mantova31 (0)2002-2006 Pro Patria120 (0)2006-2007 Pro Sesto17 (0)2007-2009 Pergocrema54 (0) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un trasferimento in prestito. ...

本表是動態列表,或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源,曾潛伏於中華民國國軍、被中國共產黨聲稱或承認,或者遭中華民國政府調查審判,為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準,正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

Gereja Santo Antonius di Campo MarzioS. Antonio in Campo Marzio (Italia)Santo António no Campo de Marte (Portugis) S. Antonii in Campo Martio (Latin)Bagian depan gereja nasional Portugal di Roma.AgamaAfiliasiKatolik RomaEcclesiastical or organizational statusGereja nasional Portugal di Roma, titulusKepemimpinanManuel José Macário do Nascimento ClementeLokasiLokasiRomaKoordinat41°54′7.1″N 12°28′28.1″E / 41.901972°N 12.474472°E / 41.901972; 12.474472Koordi...

بيلوفودسك (بالأوكرانية: Біловодськ) بيلوفودسك تاريخ التأسيس 1686 تقسيم إداري البلد أوكرانيا (24 أغسطس 1991–) [1] خصائص جغرافية إحداثيات 49°12′28″N 39°35′29″E / 49.207638888889°N 39.591277777778°E / 49.207638888889; 39.591277777778 المساحة 16.23 كيلومتر مربع الارتفاع 68 متر&...

Railway station in Yao, Osaka Prefecture, Japan Yao Station八尾駅JR-West commuter rail stationYao Station, July 2014General informationLocation3-9 Yasunaka-chō, Yao-shi, Osaka-fu 581-0085JapanCoordinates34°37′3.2″N 135°35′48.3″E / 34.617556°N 135.596750°E / 34.617556; 135.596750Owned by JR WestOperated by JR WestLine(s) Q Kansai Main Line (Yamatoji Line)Distance163.1 km (101.3 mi) from Nagoya42.2 km (26.2 mi) from KamoPlat...
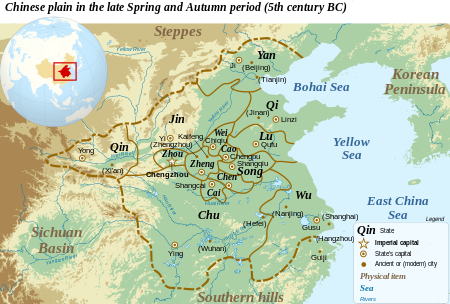
Untuk kegunaan lain, lihat jin (disambiguasi). Jin晉Abad ke-11 SM–376 SMIbu kotaTang (唐)Quwo (曲沃)Jiang (絳)Xintian (新田)Bahasa yang umum digunakanTionghoa KunoAgama Taoisme, Animisme, pemujaan nenek moyangPemerintahanMonarkiSejarah • Didirikan Abad ke-11 SM• Dibubarkan 376 SM Mata uangUang sekop Didahului oleh Digantikan oleh dnsDinasti Zhou Han (negara) Zhao (negara) Wei (negara) Sunting kotak info • Lihat • BicaraBantuan penggunaan templat ...

Based on incest taboo in a given society, certain categories of kin are forbidden to intermarryPart of a series on theAnthropology of kinship Basic concepts Family Lineage Affinity Consanguinity Marriage Incest taboo Endogamy Exogamy Moiety Monogamy Polygyny Polygamy Concubinage Polyandry Bride price Bride service Dowry Parallel / cross cousins Cousin marriage Levirate Sororate Posthumous marriage Joking relationship Clan Cohabitation Fictive / Milk / Nurture kinshi...

Island of Kiribati in the Pacific Ocean Guano Island redirects here. For another island with this name, see Guano Island (Antarctica). Main articles: Kiribati and Phoenix Islands Enderbury IslandEnderbury IslandShow map of KiribatiEnderbury IslandShow map of OceaniaEnderbury IslandShow map of Pacific OceanGeographyLocationPacific OceanCoordinates3°08′S 171°05′W / 3.133°S 171.083°W / -3.133; -171.083ArchipelagoPhoenix IslandsLength4.8 km (2.98 mi)Width...

提示:此条目页的主题不是联邦制或邦联制。 现在正式的联邦国家示意图(绿色表示)。 联邦主义(英語:Federalism)是一种一组成员联合在一起并有一个最高级治理机构的政治哲学,是國家政府與地區政府分享憲制上的主權,以及擁有不同事項的管轄權的政治體系。現在,澳大利亚、巴西和印度等都是实行联邦制的国家,而美國是實行了聯邦制最長久的國家。 類...

Sporting event delegationSão Tomé and Príncipe at theOlympicsIOC codeSTPNOCComité Olímpico de São Tomé e PríncipeMedals Gold 0 Silver 0 Bronze 0 Total 0 Summer appearances19962000200420082012201620202024 This is a list of flag bearers who have represented São Tomé and Príncipe at the Olympics.[1][2] Flag bearers carry the national flag of their country at the opening ceremony of the Olympic Games. # Event year Season Flag bearer Sport 7 2020 Summer Buly Da Conceiç...

Railway station in Pakistan Kambar Ali Khan Stationکمبر علی خان اسٹیشن کمبر علي خان اسٽيشنGeneral informationOwned byMinistry of RailwaysLine(s)Larkana–Jacobabad Light RailwayOther informationStation codeKRAK Kambar Ali Khan Railway Station (Urdu: کمبر علی خان ریلوے اسٹیشن, Sindhi: کمبر علي خان ریلوي اسٽیشن) is located in Sindh, Pakistan. See also List of railway stations in Pakistan Pakistan Railways References Exter...

Archivo Regional de la Comunidad de Madrid LocalizaciónPaís EspañaLocalidad MadridInformación generalSigla ARCMTipo Archivo regionalSede Calle de Ramírez de Prado 3, Madrid, EspañaOrganizaciónDepende de Comunidad de MadridHistoriaFundación 1993Sitio web oficial[editar datos en Wikidata] El Archivo Regional de la Comunidad de Madrid ejerce de archivo intermedio e histórico para la documentación generada por la administración autonómica de dicha comunidad. Su sede se ...

Public school district in Huxley, Iowa, United States 41°53′50″N 93°36′25″W / 41.897330°N 93.607067°W / 41.897330; -93.607067 Ballard Community School DistrictLocationHuxley, IowaStory, Boone, and Polk counties United StatesCoordinates41.897330, -93.607067District informationTypeLocal school districtGradesK-12SuperintendentDani TrimbleSchools4Budget$28,508,000 (2020-21)[1]NCES District ID1904200[1]Students and staffStudents1969 (2022-23)[...
Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari Freeview (Britania Raya) di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai bahasa aslinya, harap pertimbangkan untuk menelusuri referensinya dan menyempurnakan terjemahan ini. Anda juga dapat ikut bergotong royong pada ProyekWiki Perbaikan Terjemahan. (Pesan ini dapat dihapus jika terjemahan dirasa sudah cukup tepat. Lihat pula: panduan...














