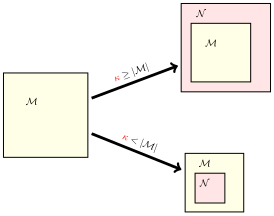
Теорема Лёвенгейма — Скулема
| |||||||||||
Read other articles:
Frank ThringThring saat pengambilan gambar dari film King of KingsLahirFrank William Thring(1926-05-11)11 Mei 1926Melbourne, Victoria, AustraliaMeninggal29 Desember 1994(1994-12-29) (umur 68)Melbourne, Victoria, AustraliaPekerjaanPemeranSuami/istriJoan Cunliffe (bercerai) Frank William Thring (11 Mei 1926 – 29 Desember 1994) adalah seorang pemeran radio, panggung, televisi dan film asal Australia.[1] Masa kecil Thring lahir di Melbourne, putra dari pasangan Frank...

Map all coordinates using OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) GPX (secondary coordinates) This list is of the Intangible Cultural Properties of Japan in the Prefecture of Okinawa.[1] National Cultural Properties As of 1 January 2015, eleven Important Intangible Cultural Properties have been designated, being of national significance.[2][3][4] Performing Arts Property Holder Comments Image Ref. Kumi Odori�...

Indah NevertariLahirIndah Nevertari11 Mei 1992 (umur 31)Medan, Sumatera Utara, IndonesiaPekerjaanPenyanyiDikenal atasRising Star Indonesia (musim pertama) (2014)Karier musikAsalMedanGenrePopHip-hopRapRnBInstrumenVokalTahun aktif2014–sekarangLabelWarner (2014-2017)Athena Jaya Indah Nevertari (lahir 11 Mei 1992) adalah seorang penyanyi asal Kota Medan, Sumatera Utara, Indonesia. Ia dikenal sebagai juara pertama Rising Star Indonesia (musim pertama) pada tahun 2014 yang ditayangkan stasi...

Trouble MakerAlbum mini karya Trouble MakerDirilis01 Desember 2011 (2011-12-01)Direkam2011GenrePop, danceDurasi13:25LabelCube EntertainmentUniversal Music KoreaProduserShinsadong TigerKronologi Trouble Maker Trouble Maker(2011) Chemistry(2013) Singel dalam album Trouble Maker Trouble MakerDirilis: 1 Desember 2011 Chemistry2013 Trouble Maker (Korean: 트러블메이커) adalah album debut dari subunit co-ed Trouble Maker yang terdiri dari HyunA dari 4Minute dan Hyunseung dari Beast (a...

Halaman ini berisi artikel tentang wilayah Indonesia di pulau bernama sama. Untuk pulau tersebut, lihat Kalimantan. Untuk kegunaan lain, lihat Kalimantan (disambiguasi). Kalimantan Wilayah Negara Indonesia Provinsi Kalimantan Tengah, Kalimantan Timur, Kalimantan Utara, Kalimantan Selatan, Kalimantan Barat, Ibu Kota Nusantara Kota Pontianak, Singkawang, Palangka Raya, Banjarbaru, Banjarmasin, Balikpapan, Bontang, Samarinda, Tarakan Titik tertinggi Bukit Raya - lokasi Taman Nas...

American police chief in Los Angeles This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Michel Moore – news · newspapers · books · scholar · JSTOR (December 2021) (Learn how and when to remove this...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Csobaj – news · newspapers · books · scholar · JSTOR (July 2016) (Learn how and when to remove this template message) Place in Borsod-Abaúj-Zemplén, HungaryCsobaj Coat of armsCsobajCoordinates: 48°02′56″N 21°20′09″E / 48.048961°N 21.335769°E...

Borough in Morris County, New Jersey, US Borough in New JerseyFlorham Park, New JerseyBorough200-year-old oak tree at Brooklake Country Club SealLocation of Florham Park in Morris County highlighted in red (right). Inset map: Location of Morris County in New Jersey highlighted in orange (left).Census Bureau map of Florham Park, New JerseyFlorham ParkLocation in Morris CountyShow map of Morris County, New JerseyFlorham ParkLocation in New JerseyShow map of New JerseyFlorham ParkLocation in the...

Social class; person who performs intellectual labor Office workers A white-collar worker is a person who performs professional service, desk, managerial, or administrative work. White-collar work may be performed in an office or other administrative setting. White-collar workers include job paths related to government, consulting, academia, accountancy, business and executive management, customer support, design, economics, engineering, market research, finance, human resources, operations r...

Disambiguazione – Se stai cercando altri significati, vedi Eclissi (disambigua). Disambiguazione – Eclisse rimanda qui. Se stai cercando la lampada progettata da Vico Magistretti, vedi Eclisse (lampada). Disambiguazione – Eclissi totale rimanda qui. Se stai cercando altri significati, vedi Eclissi totale (disambigua). Eclissi solare del 1999. L'alone luminoso intorno al disco solare eclissato è la corona solare. Esempio di eclissi di una stella binaria L'eclissi, o...

1937 film Tomb of the AngelsDirected byCarlo Ludovico BragagliaWritten byCurt Alexander Carlo Ludovico Bragaglia Cesare Ludovici Roberto RosselliniProduced byFrancesco SalviStarringAmedeo Nazzari Luisa Ferida Antonio GradoliCinematographyMario AlbertelliEdited byFerdinando Maria PoggioliMusic byEnzo MasettiProductioncompanyDiorama FilmDistributed byLux FilmRelease date 1937 (1937) Running time84 minutesCountryItalyLanguageItalian Tomb of the Angels (Italian: La fossa degli angeli) is a 1...
周處除三害The Pig, The Snake and The Pigeon正式版海報基本资料导演黃精甫监制李烈黃江豐動作指導洪昰顥编剧黃精甫主演阮經天袁富華陳以文王淨李李仁謝瓊煖配乐盧律銘林孝親林思妤保卜摄影王金城剪辑黃精甫林雍益制片商一種態度電影股份有限公司片长134分鐘产地 臺灣语言國語粵語台語上映及发行上映日期 2023年10月6日 (2023-10-06)(台灣) 2023年11月2日 (2023-11-02)(香�...

Norwegian government agency Emblem of the County Governors Politics of Norway Constitution Monarchy King Harald V Crown Prince Haakon Government Council of State (current cabinet) Prime Minister (list) Jonas Gahr Støre List of governments Parliament Storting President: Masud Gharahkhani Norwegian Parliamentary Ombudsman Political parties Politicians Recent elections Parliamentary: 2021201720132009 Local: 2023201920152011 Local government Administrative divisions Counties (Fylker) Municipalit...

European Parliament political group This article is about the current European Parliament Group. For the europarty established in 1992, see Party of European Socialists. S&D redirects here. For other uses, see S&D (disambiguation). Progressive Allianceof Socialists and DemocratsEuropean Parliament groupNameProgressive Allianceof Socialists and DemocratsEnglish abbr.S&D[1](23 June 2009 – present) Older: PES[2](21 April 1993[3] – 22 June 2009)SOC[2 ...

This is a complete list of episodes for the Japanese anime series Yu-Gi-Oh! Duel Monsters GX (changed to simply Yu-Gi-Oh! GX in the 4Kids dub, due to the previous anime not using Duel Monsters in the title), based on the Yu-Gi-Oh! Duel Monsters anime. There are four different music themes set accompanying the opening animation and ending credits. For episodes 1-33, they are Rising Weather Hallelujah for the opening animation and Genkai Battle for the ending credits. From episode 34 through t...

British pay television channel Television channel Sky CrimeLogo used since 2020ProgrammingPicture format1080i HDTV(downscaled to 16:9 576i for the SDTV feed.)Timeshift serviceSky Crime +1OwnershipOwnerSky Group (Comcast)Sister channelsList of Sky UK channelsHistoryLaunched1 October 2019; 4 years ago (2019-10-01)ReplacedReal LivesLinksWebsitewww.sky.com/watch/channel/sky-crimeAvailabilityTerrestrialBTChannel 349Channel 364 (HD)Streaming mediaSky GoWatch live (UK and Ireland o...

Questa voce o sezione sull'argomento Guinea Equatoriale non cita le fonti necessarie o quelle presenti sono insufficienti. Commento: Diverse affermazioni senza fonte Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Guinea Equatoriale (dettagli) (dettagli) Unidad, Paz, Justicia Guinea Equatoriale - Localizzazione Dati amministrativiNome completoRepubblica della Guinea Equatoriale Nome ufficiale(ES) República de Guinea Ec...

American college football season 2017 NC State Wolfpack footballSun Bowl championSun Bowl, W 52–31 vs. Arizona StateConferenceAtlantic Coast ConferenceDivisionAtlantic DivisionRankingCoachesNo. 23APNo. 23Record9–4 (6–2 ACC)Head coachDave Doeren (5th season)Offensive coordinatorEliah Drinkwitz (2nd season)Offensive schemeMultipleDefensive coordinatorDave Huxtable (5th season)Base defense4–3Home stadiumCarter–Finley StadiumSeasons← 20...

قطاع غزّة هو المنطقة الجنوبية من السهل الساحلي الفلسطيني على البحر المتوسط؛ على شكل شريط ضيق شمال شرق شبه جزيرة سيناء، وهي إحدى منطقتين معزولتين (الأخرى هي الضفة الغربية) داخل حدود فلسطين الإنتدابية لم تسيطر عليها القوات الصهيونية في حرب 1948، ولم تصبح ضمن حدود دولة إسرائيل...

この記事には参考文献や外部リンクの一覧が含まれていますが、脚注による参照が不十分であるため、情報源が依然不明確です。 適切な位置に脚注を追加して、記事の信頼性向上にご協力ください。(2023年3月) 砲艦(ほうかん)は、軍艦の一種であり、比較的小型で主として沿岸・河川・内水で活動する、火砲を主兵装とした水上戦闘艦艇の事を指す。英語ではGunboat...